 |
|
|
[Sponsors] | |||||
Plot Turbulence Spectrum Using 2D Spatial FFT |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 | |
|
New Member
Jeffrey Johnston
Join Date: Oct 2020
Location: Belfast, Northern Ireland
Posts: 21
Rep Power: 5  |
Hello!
I am trying to replicate the results of a study (here) that performs LES of an atmospheric boundary layer. One of the results produced is a turbulence spectrum. I want to recreate this, but I'm a bit lost. Here's the description in the paper: Quote:
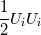 before performing the FFT. But in this paper, the (horizontal) velocity magnitude is calculated instead, before performing the FFT. But in this paper, the (horizontal) velocity magnitude is calculated instead, 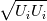 . So, have I misunderstood the turbulence spectrum? Does the -5/3 slope region exist in a a spectral transform of the magnitude of the velocity? And will it exist for only the horizontal magnitude? Do we have to assume that the vertical component is negligible here (a reasonable assumption in this case)? . So, have I misunderstood the turbulence spectrum? Does the -5/3 slope region exist in a a spectral transform of the magnitude of the velocity? And will it exist for only the horizontal magnitude? Do we have to assume that the vertical component is negligible here (a reasonable assumption in this case)?My second point of confusion is how to obtain a single 2-axis plot from a 2D fft. Performing a fft of the 2D array of velocity magnitudes produces a 2D array of velocity intensities. I assume that this resultant array is what the we call "wavespace"? But what is a wavevector? How do I find ones of equal magnitude and sum them? And what are the concentric rings all about? Many thanks, |
||
|
|

|
||
| Tags |
| fft, les, spectral analysis, turbulence, waves |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| How to plot time dependent energy spectrum | Falu | Main CFD Forum | 21 | January 16, 2021 08:41 |
| Plot the Energy Spectrum | Elyas_Mosibat | OpenFOAM Post-Processing | 14 | June 3, 2019 13:46 |
| Amplitude spectrum of temperature fluctuations | selvam2487 | CFX | 0 | March 16, 2014 13:59 |
| energy spectrum using FFT | kharnabnew | FLUENT | 0 | November 18, 2009 03:16 |
| Discussion: Reason of Turbulence!! | Wen Long | Main CFD Forum | 3 | May 15, 2009 09:52 |