 |
|
|
[Sponsors] | |||||
How to calculate and assemble a Jacobian matrix for Compressible Euler solver? |
 12Likes
12Likes
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Sayan Bhattacharjee
Join Date: Mar 2020
Posts: 495
Rep Power: 8  |
Hello everyone,
I was reading this paper ( https://doi.org/10.1016/j.jcp.2018.04.005 ) and trying to implement it. I understand most of the paper, except how they're trying to assemble the global Jacobian matrix in section 3.5, as shown in the attached image flux.png. They derived the equation for the Jacobian A before, as shown in the attached image jacobian.png, and I understand it. But while trying to assemble the global Jacobian matrix, they introduce two new terms 1. J(i,i) = dRi/dUi : which is supposedly the Jacobian with respect to the solution vector in volume i 2. J(i,j) = dRi/dUj: which is supposedly the Jacobian with respect to the solution vector in neighbor volume j DOUBT-1: I don't know how on calculate these two Jacobians. I understood the derivation of the basic Jacobian, but don't get how we can calculate (dRi/dUj) i.e derivative of the residual of cell i, with respect to solution in cell j. DOUBT-2: I don't know how to assemble the local Jacobians into the global Jacobian. In FEM, it is often compulsory to mention how the stiffness matrices are assembled, and the matrix pattern formed is often discussed at very great depth, and details. Especially, they go at great lengths to explain if components of the stiffness matrices will overwrite or add to each other when assembled in a global form. For Multiphysics FEM papers, they even explain how the contribution of the different physics equations will be inserted into the global form. This is shown in the attached image fem.png, which shows contribution of electromagnetics and structural deformation. Unfortunately in this paper, the picture of the assembled global Jacobian only shows a basic matrix, which we can't even tell, if its sparse, or dense. Maybe it's something easy to do in view of the author, but since they didn't give a reference to any other paper or book on how to do this assembly, makes it little bit more difficult for me to understand. I'm thinking of just emailing the authors to request for clarifications if nothing else works. PS: The iterative solver they used, is Gauss-Siedel, which I also respectfully don't agree with. A Krylov solver would've been significantly better. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
Hello,
About doubt 1: Eq 3.23 and 3.24 are the numerical flux derivatives, you have to differentiate the Roe flux of eq 3.4. Note that the first two terms of eq 3.4, are readily obtained thanks to eq 2.7. What is not mentionned (but I really overlooked) in the paper is how they compute the derivatives of the remaining term in eq 3.4. There are mainly three ways of doing that: - hand differentiation - finite differencing - automatic differentiation Hand differentiation is tedious. Finite differentiation is subject to round-off and costly, unless if you use it in the frame of matrix-vector based linear solvers, e.g. Krylov solvers. Automatic differentiation is exact but requires either an external library or some coding: https://www.sciencedirect.com/scienc...21999119306473 doubt 2: Did you have a look to the book of Blazek section 6.2: COMPUTATIONAL FLUID DYNAMICS: PRINCIPLES AND APPLICATIONS. |
|
|
|

|
|
|
|
|
#3 | |
|
Senior Member
Sayan Bhattacharjee
Join Date: Mar 2020
Posts: 495
Rep Power: 8  |
Quote:
No wonder I couldn't figure out how to do this on my own. The paper doesn't even mention anything regarding how they solved it, or I missed it somehow. I'm seeing Automated Differentiation as a good solution to this problem. Though is it possible to use Symbolic Differentiation to generate the exact derivative formulas of this kind of complexity? If it is possible to symbolically derive the derivative equations, I would be also okay with manually coding the derived equations directly. Thanks! I will get back after I do some studying on this topic. |
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
For development purposes I often use formal calculus softwares and their "ready to use" c or fortran export. I can't tell for such complicated functions, the resulting expressions may be very verbose.
There's also this reference where they explicitly give Jacobians for various approximate Riemann solvers, maybe helpful maybe not: https://www.sciencedirect.com/scienc...21999114002459 As far as automatic differentiation is concerned, the price ticket is higher, you will need some coding. But in the long run it is a clear winner. Indeed, if you hand write and code the derivatives, what happens when you want to implement a different Riemann solver or an other equation of state ? This is something to have in mind. |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Sayan Bhattacharjee
Join Date: Mar 2020
Posts: 495
Rep Power: 8  |
Update: I understood little bit more about the topic.
The paper apparently uses hand derived equations from Dr. Nishikawa's book. They mention this in a single line, so I missed it earlier. I had little difficulty understanding at first, but it seems like, similar to automatic differentiation, Dr. Nishikawa also used a number of chain rule based derivatives to calculate the numerical derivatives. I still have to study a lot more about this, but the basics seem clear to me. One possible limitation I see is, the number of matrix-vector multiplications required in the chain rule can make things little bit slow, but its acceptable to me for now. I have a few doubts, but I will probably ask them later. Thanks! |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Sayan Bhattacharjee
Join Date: Mar 2020
Posts: 495
Rep Power: 8  |
Oh wow!
Dr. Nishikawa even gave the full matrix formed due to the chain derivatives. Just using this matrix directly would be enough, and most definitely what the paper also used. Really cool! |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
From the same author, you may find useful the fortran subroutines for the Roe flux differentiation. He also compares the analytical expressions with those obtained from automatic differentiation via operator overloading:
http://www.cfdbooks.com/ In section free codes, "How to compute flux Jacobians" |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Sayan Bhattacharjee
Join Date: Mar 2020
Posts: 495
Rep Power: 8  |
Okay, I think I understand how the Global Jacobian (K) will look and be assembled.
1. K will be a sparse block matrix of size N*N, where each element will be a block of size 5x5. It's a little confusing to explain like that, but its the convention followed AFAIK. 2. Each i'th row of K corresponds to the linear equations of the i'th Control Volume (CV). 3. Each i'th row of K means the Jacobian of the residual i.e how the residual changes w.r.t the changes in the left and right Riemann states in the current i'th CV, and the j'th neighbor CV. 4. Since the Riemann state depends on neighbor cells, so each row of K should have the J(i,i) Jacobian at location (i,i), and the J(i,j) Jacobian at location (i,j). 5. Each local Jacobian J(i,j) and J(i,i) is a 5x5 dense matrix. 6. J(i,i) only contributes to the diagonal elements of K. 7. J(i,j) only contributes to the off-diagonal elements of K. 8. The Jacobian can be 1st order accurate, so we only need the immediate neighbors of the i'th CV, so our computational stencil/molecule will be small, and the K matrix will be extremely sparse. In the end, the K matrix will look like this, where each dot is a 5x5 matrix. PS: I have some doubts on how boundary conditions affect the Jacobian matrix, but I have to study more before asking ... |
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
Formulated an other way, on a practical side:
If you loop through the faces of your mesh, on a face which separates control volumes i and j, with normal pointing from i to j, and assuming a first order Jacobian: - You compute your flux F(Qi,Qj) and derivatives dFdQi, dFdQj - The sum of fluxes is updated this way: SumFlux_i=SumFlux_i+F, SumFlux_j=SumFlux_j-F, this will form your residual - Your global Jacobian is updated this way: J(i,i)=J(i,i)+dFdQi, J(j,i)=J(j,i)-dFdQi, J(i,j)=J(i,j)+dFdQj, J(j,j)=J(j,j)-dFdQj i and j in the Jacobian matrix are interior cells. At a boundary, let's assume i is interior and j a boundary: dFdQi is not sent to J(j,i): this position does not exist in the matrix. Similarly for J(i,j) and J(j,j). So at a boundary where i is interior, only the derivative dFdQi is computed to update J(i,i). |
|
|
|

|
|
|
|
|
#10 | |
|
Senior Member
Sayan Bhattacharjee
Join Date: Mar 2020
Posts: 495
Rep Power: 8  |
Quote:
For these three steps, do you know of books/chapters/papers that explains this processes in much more details for implicit solvers? I understand the process, but just want to have a good reference to ensure everything is implemented correctly. |
||
|
|

|
||
|
|
|
#11 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
Hello,
Well apart from the Blazek book I mentionned above I do not have other detailed references. But given your last comments, I think you already got most of the ingredients needed. You would most likely learn the last bits by trying to solve implicitly some increasingly difficult equations: - 1D scalar linear advection - 1D scalar burger's equation - 1D system of Euler equations - 2D structured system of Euler equations - 2D unstructured scalar linear advection - 2D unstructured system of Euler equations I think of two ways of verifying your implicit implementation - Replace your derivatives by finite differences, dFdQi=(F(Qi+eps,Qj)-F(Qi,Qj))/eps (with a careful choice of eps) - Look for a problem with a steady solution, say NACA0012 at subsonic conditions. Solve with 1st order Jacobian and residual. In the limit of infinite dt, the implicit time step tends to a Newton step. Your residual should vanish quadratically, e.g. steady solution obtained in less than 10 iterations. Note that the linear system will be difficult to converge due to lower diagonal dominance and the initial solution should not be too far away from the final solution. |
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
Sayan Bhattacharjee
Join Date: Mar 2020
Posts: 495
Rep Power: 8  |
Update ...
1. Figured out how to calculate the Roe flux using Roe-Pike method from Toro's book, and how to apply Harten's entropy fix to the wave speeds. I'm 99% sure I can implement it correctly. 2. Figured out how to calculate the RHS residuals and subtract/add them to cells. One thing I don't understand is .. if the Harten entropy fix will need to be included in the Jacobians J(i,i) and J(i,j) also? PS: I have little bit more doubt on how to calculate the Jacobians J(i,i), and J(i,j), but I have to study more on my own before asking any questions. |
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
Consider the 1D time dependent 1st order spatial/temporal implicit FV form of the Euler equations:
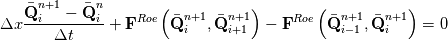 You can view this system as a root-finding problem, looking for the solution at the next time-step 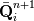 : :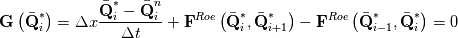 With Newton algorithm, you iterate the following: 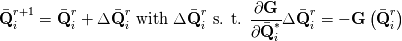 At convergence, you get 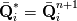 Grouping Roe flux derivatives in the term 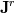 , your Newton iteration reads: , your Newton iteration reads: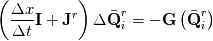 Assume you perform only one Newton iteration. At the first Newton iteration, you need a guess value. Take this guess value as the last time-step value 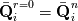 . Doing that the first term of function . Doing that the first term of function 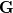 vanishes and you end up solving at each time-step: vanishes and you end up solving at each time-step: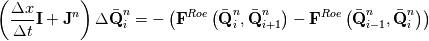 This is nothing more than the classical linearized BDF1 scheme that you could have obtained directly from the first equation by deriving Taylor expansion of the fluxes and neglecting 2nd order terms. Now if you let 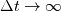 , the last equation reduces to a Newton iteration for the steady-state Euler equations: , the last equation reduces to a Newton iteration for the steady-state Euler equations: 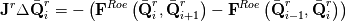 Because of this connection, you see that the Jacobian matrix should be theoretically exact to reach the steady-state in a minimum amount of iterations (hopefully quadratically). However, this last system is hard to solve numerically. First because you know that Newton needs a good first guess to avoid divergence and second because the linear system lacks diagonal dominance and hence linear solvers converge slowlier. It gets even worse when 2nd order spatial discretization comes into play. First the exact Jacobian matrix gets denser because of the dependence of the flux on more neighbours and second the condition number gets higher. This is why usually, for steady-state problems, the last form is prefered: 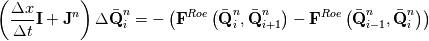 In this case, the Jacobian does not need to be exact. It is a tradeoff to find between 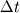 and the convergence rate of the linear solver. and the convergence rate of the linear solver.
|
|
|
|

|
|
|
|
|
#14 |
|
Senior Member
Sayan Bhattacharjee
Join Date: Mar 2020
Posts: 495
Rep Power: 8  |
Thanks.
For now I'm just going to use Finite Difference Method to create the Jacobian, with h = sqrt(machine epsilon). It seems to be much more safer than using the analytical Jacobian. Also I somewhat understand the boundary conditions now. They're just added as fluxes. On a conceptual level, I understand most of the things. The only thing left to do, is to implement them. |
|
|
|

|
|
|
|
|
#15 |
|
Senior Member
Sayan Bhattacharjee
Join Date: Mar 2020
Posts: 495
Rep Power: 8  |
Update: The explicit solver works correctly, along with the flux, boundary conditions, gradients, limiters, and local timestepping.
The results are shown below. I'm now implementing the Implicit code, and I guess, had a few doubts ... 1. For the FDM method of computing the Jacobian, I'm seeing them use the formula dF/dh = (F(x+dh) - F(x)) / dh This is easy to understand for 1D case, where F is dependent on only a single variable x, but for residuals, we depend on left and right states Ui, and Uj. i.e Ri = Ri(Ui,Uj) ... Question: So should our equation be like this? J(i,i) = dRi/dUi = (R(Ui+dh,Uj) - R(Ui,Uj)) / dh , and ... J(i,j) = dRi/dUj = (R(Ui,Uj+dh) - R(Ui,Uj)) / dh The bold/italic terms shows where I think we'd need to add the perturbation dh and compute the local Jacobian. As I understand now, the Jacobian is a mathematical formulation to show how the output (residual) changes due to some perturbation in the inputs (Ui, Uj) so this seems correct to me. I'm just directly using the residuals to compute the Jacobian, instead of fluxes, and the boundary conditions are set inside the method to compute residuals, so their effect are also introduced in the Jacobian. Thanks! |
|
|
|

|
|
|
|
|
#16 | |
|
Senior Member
Sayan Bhattacharjee
Join Date: Mar 2020
Posts: 495
Rep Power: 8  |
Quote:
Thanks for all your help.  I finished the Implicit solver, and it works perfectly. For CFL = 55, the residuals drop to 1E-4 within 100 iterations. I decide to use Rusanov flux, and create the Jacobian with FDM based approach for now. |
||
|
|

|
||
|
|
|
#17 |
|
Senior Member
Join Date: Oct 2011
Posts: 242
Rep Power: 16  |
Well done !
Don't you reach lower residuals for higher iteration count ? You may try to ramp up the CFL and see if your residual curve gets steeper. How do you solve the linear system ? Do you construct the whole matrix with finite differencing or a matrix-vector product inside a krylov method ? |
|
|
|

|
|
|
|
|
#18 | |
|
Senior Member
Sayan Bhattacharjee
Join Date: Mar 2020
Posts: 495
Rep Power: 8  |
Quote:
 The residuals indeed drops more, if we do more iterations. After 500 iterations, the residuals for the 4 equations respectively are: [5.370326e-13, 6.514204e-10, 9.222502e-11, 4.112054e-07] Increasing the CFL does help, but the gains in convergence speed seems to be small after a certain limit. I tried to ramp up the CFL to 100, then 250, then 1000, and all of them converge, but the rate of convergence does not increase too much. For CFL of 250, the density residual drops to 1E-6 after 100 iterations, but after that, increasing CFL doesn't really seem to help much. I think it's because our Jacobian itself is 1st order, and somewhat inaccurate, so just ramping up CFL doesn't help in achieving quadratic convergence that Newton methods are famous for. I solve the linear system currently with a Sparse LU direct solver. Since this is just an experimental code, and I want to debug and validate my code easily, I used a direct solver. For the final industrial strength code, I want to use iterative solvers and preconditioners available in PETSc. The local Jacobian matrices are created using the FDM method. Then we assemble them to the global Jacobian matrix. To reduce computation time, I calculate the local Jacobians from the left cell, and reuse them to create the local Jacobians for the right cell. This was possible since, I was able to derive and prove that 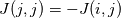 and and 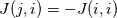 . .I don't want to use Automatic Differentiation right now, because FDM based method seems to be accurate enough for many problems in CFD, and even PETSc uses it. So, to save time, I will keep using this for now. PETSc apparently has a Jacobian Free Newton Krylov method, so after I learn more about PETSc, I will try to use it if possible. |
||
|
|

|
||
 |
| Tags |
| euler, flux, jacobian, solver |
|
|