 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Alps
Join Date: May 2009
Posts: 4
Rep Power: 16  |
Hi,
I am doing a multiphase simulation with phase change, for Liquid N2 in a tube. The Re=2043, Ja=0.42, Pr=2.32 based on liquid N2 properties. Liq N2 enters at 77K, while the wall is at 300K. So film boiling occurs at N2 surface. Assumptions in the model: 2d axisymmetric, incompressible, constant property, laminar flow. Although not completely justified, this is the best I can do right now, since its a DNS. Grid used is 750x50. Computational domain: 40x0.5. dt=0.001 This is a DNS with separate equations for the two phases, which are matched at the interface via the interfacial conditions. The problem I am facing is that I am getting a weird velocity field. The best way i can describe it is checkerboard. it occurs only in a small region in the vapor, where velocity is very high, and Re > 20000. My question is: is this a numerical instablity, or is this what happens when u try to simulate a turbulent flow with laminar assumption? I am using CDS, with explicit treatment of convective terms, and diffusion terms are treated using Crank Nicholson. CFL number is 1.7 in the same region above. I tried to decrease the time steps, but the velocity field is quite oscillatory (wrt space) Strange thing is, the divergence and press residuals are quite low. 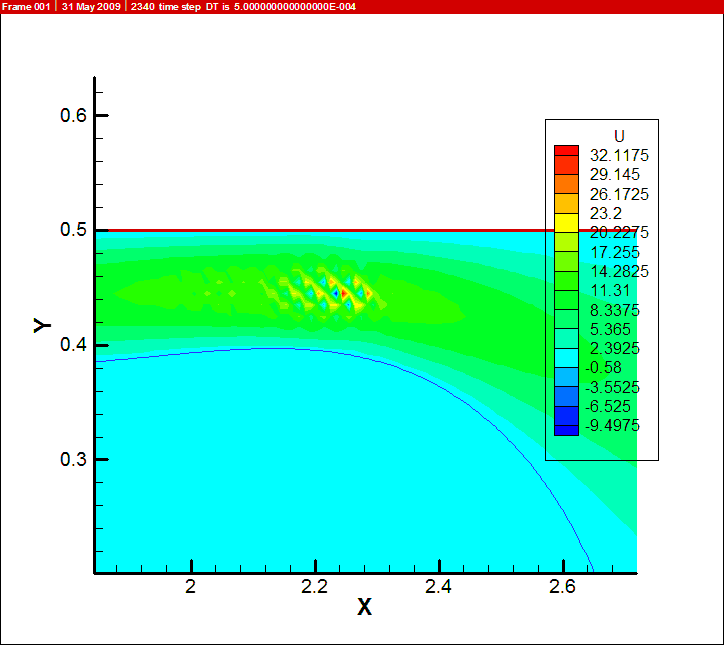
|
|
|
|

|
|
|
|
|
#2 |
|
New Member
Alps
Join Date: May 2009
Posts: 4
Rep Power: 16  |
The oscillations are occurring purely in the vapor phase, and have nothing to do with the interface. The only role the interface plays is in generating the mass transfer which leads to high velocities in that constriction region.
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
N/A
Join Date: Mar 2009
Posts: 189
Rep Power: 17  |
Aliasing errors occurs when you use high-order CDS without dissipation. Try to use the Skew-Symmetric form of the convection term to avoid this error. The checkerboard pattern usually occurs due to the lack of dissipation in CDS. You can avoid that by using a staggered grid instead of a collocated one. Another option is to use higher order upwind scheme like those used by Moin for DNS studies. Also keep Courant number less than 1.0 to avoid any error in accurately predicting the small scale motions.
|
|
|
|

|
|
|
|
|
#4 |
|
New Member
Alps
Join Date: May 2009
Posts: 4
Rep Power: 16  |
@momentumwaves the red and blue dots u see in the field correspond to neighboring mesh points...ie, the oscillations are at the scale of adjacent nodes. i think u r right, the effect seems to be numeric
decreasing the mesh size will make the CFL constraint more severe.... @harishg could you let me know what you mean by skew-symmetric form of convective term or point me to some references? I am using second order central difference for CDS, i guess it does not have dissipation. also second order Adam's Bashforth scheme to adavance to unsteady equation. Unfortunately, i am constained to use collocated grid, since due to the presence of the interface, i run into complex geometries near the interface. I am using the formulation by Zang, Street et al 1994. I tried to reduce the time step to keep Courant number low, but that only delays the onset of instability a little, since the velocity in that region increases continuously. I thank you both for your responses and suggestions. 
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
N/A
Join Date: Mar 2009
Posts: 189
Rep Power: 17  |
Second order central difference scheme and DNS may not be a best combination since the dissipation might be very high but that again depends on the grid you use.
Look here: http://www.channelflow.org/dokuwiki/doku.php/docs in the userguide for the skew symmetric form of the convection term. |
|
|
|

|
|
|
|
|
#6 |
|
New Member
Alps
Join Date: May 2009
Posts: 4
Rep Power: 16  |
Hello all, sorry for the delay in responding.
@ anon_h i think you may be right, after some new results i think it is not the CFL number but the Peclet number causing the trouble. Crank Nicholson should make the numerical scheme stable for all time steps, only limited by accuracy. It is the Peclet number which is direcly related to the convection term (CDS used). so refining the grid will alleviate the Peclet number @harishg i think there may be some confusion due to my use of the term DNS. all i meant was that it does not use any models. it is not a turbulence simulation. there is no turbulence modelling. but its a strongly convective pipe flow. so cds may be causing the problem thanks both for your suggestions. i will let you know if anything works out. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Thermal phase change model | Piti | CFX | 1 | January 14, 2021 10:03 |
| Solid/liquid phase change | fabian_roesler | OpenFOAM | 10 | December 24, 2012 06:37 |
| Two phase flow with phase change | Ahmad Al-Zoubi | CFX | 1 | November 26, 2008 03:59 |
| thermal phase change question | CFDflying | CFX | 1 | February 18, 2004 04:10 |
| compressible two phase flow in CFX4.4 | youngan | CFX | 0 | July 1, 2003 23:32 |