 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Caner
Join Date: Jan 2010
Posts: 8
Rep Power: 16  |
Hello everyone,
I am researching on jet impingement systems.I carry out numerical analysis to investigate flow field at the confined channel where dual jets impinge.I have a basic question about deciding characteristic length. Basic drawing of my dual Nozzle can be seen here.There are 2 nozzles, one is(smaller diameter one-D1) in the another one(bigger diameter one-D2). One of the parameter of my numerical simulation is Velocity ratio "VR" which means the ratio of V1 / V2.So in the case of VR=0,0.5,1.5,2,(which means V1 and V2 has a different velocity value) the question arises; If there are two different velocities (V1 and V2) how should I determine the the characteristic length and Reynolds number in order to conduct numerical simulation? Thank you very much in advance! Regards, Caner   
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Andrew
Join Date: Mar 2009
Location: Washington, DC
Posts: 209
Rep Power: 18  |
can you not use the respective diameter of the nozzle to determine your Re?
and, since the mdot doesn't change I would use Re = (4*mdot)/(mu*pi*Diam) |
|
|
|

|
|
|
|
|
#3 | |
|
New Member
Caner
Join Date: Jan 2010
Posts: 8
Rep Power: 16  |
Quote:
I think, I can use D2-D1 as a characteristic length in my numerical analysis like other annular impinging jet studies did, but that D2-D1 cant be used to determine inner jet's reynolds number. and could you please explain what mdot is? |
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
Andrew
Join Date: Mar 2009
Location: Washington, DC
Posts: 209
Rep Power: 18  |
mdot is mass flow rate. I didn't see that diagram before my first post, so unless you know the mass flow rate thru the inner and outer channels you might not be able to use that.
|
|
|
|

|
|
|
|
|
#5 |
|
New Member
Shashank
Join Date: Jul 2010
Posts: 18
Rep Power: 15  |
Hi,
I am conducting investigations into impinging jets as well. Most literature gives Re values used. For purpose of validation, I need to mimic these exact conditions, for that I wanted to know how to deduce the diameter value using the provided Re number. The problem is both flow rate (or velocity) and diameter values are unknown, how can I go about this problem. Please help. |
|
|
|

|
|
|
|
|
#6 |
|
Member
Dan
Join Date: Oct 2010
Location: UK
Posts: 41
Rep Power: 15  |
Hi
Caner you could simply switch to using the dimensional form of the equaions, and calculate your flow in real space, rather than non dimensional space. That way the viscous term of your equatons depends on viscosity rather than Re. Azurespirit, it sounds like your bench mark solution is in non dimensionl form. In which case if you are solving with the dimensionless from of the equations, your velocity and charecteristic length will both be 1. |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Andrew
Join Date: Mar 2009
Location: Washington, DC
Posts: 209
Rep Power: 18  |
I think you just want to keep the Re the same - Reynolds Scaling, so you don't need to know any diameter or length. If you pick a diameter you will know what velocity you need to get the Re required.
|
|
|
|

|
|
|
|
|
#8 |
|
New Member
Shashank
Join Date: Jul 2010
Posts: 18
Rep Power: 15  |
@dandalf
i dont think i can consider both diameter and velocity as 1 since i wont possibly obtain the desired Re number @mettler yeah that's what i've figured. it basically scales down to Re=v.d/constant so maintain a v/d ratio to get the desired Re. thanks anyway. |
|
|
|

|
|
|
|
|
#9 |
|
Member
Dan
Join Date: Oct 2010
Location: UK
Posts: 41
Rep Power: 15  |
Re is defined as,
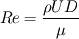 presumably you are solving a set of continuity equations of the form, 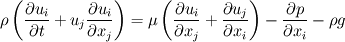 Which is the dimensional form of the navier stokes equation for the conservation of momentum. However, if you non dimensionalize this, i.e. set 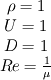 giving the incompressible non dimensional from of of the equation, 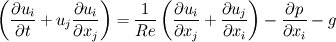 this is the form of the equation found in many books, but is only valid if your computational domain has, characteristic distance 1, velocity 1, and density 1. I got tripped up by this myself, Most bench mark solutions will be presented in this dimensionless form for obvious reasons. Hope this helped, Dandalf |
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Join Date: Feb 2010
Posts: 148
Rep Power: 17  |
I would use the length that gives you the largest Reynolds number and thus the smallest boundary layers. This way, I think that you can be sure to resolve all boundary layers. Good luck!
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Turbulent Characteristic Length/Turbulent Length Scale | fluentnoob | FLUENT | 2 | July 3, 2009 08:40 |
| Characteristic length scale | Linfeng | Main CFD Forum | 0 | January 9, 2004 22:51 |
| characteristic Length | CFD MAN | Main CFD Forum | 3 | September 11, 2002 07:26 |
| Characteristic Length | CFD MAN | FLUENT | 0 | August 19, 2002 21:40 |
| Characteristic Length Scale | Thomas P. Abraham | Main CFD Forum | 2 | April 20, 1999 17:16 |