 |
|
|
[Sponsors] | |||||
Linear analytical solution oto the 2D free sloshing water surface elevation |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
|
Hi, all
Does anyone know about the linear (the simplest) analytical solution to free sloshing water surface elevation? Many people have simulated free sloshing water problem as a validation for free surface modeling. As far as I know, the inviscid flow free sloshing in a 2D still rectangle tank is the simplest case. The motion can be approximated by the linear wave theory. And the solution expression can be pretty simple. With free surface starting from a constant slope as initial BC, I found from some paper the following equation: 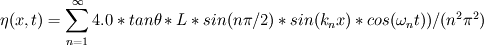 in which 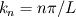 and and 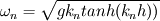 L is the tank length, h is the still water depth and 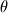 is the initial free surface slope. is the initial free surface slope. I wonder if the above expression has kind of typo or missing something, as it introduces some obvious wiggles when I plotted it, which should not appear in a li near solution. So can anyone point out if this is a correct expre ssion? If not, where is wrong? Where can I find a correct one? Thank you. |
|
|
|

|
|
|
|
|
#2 |
|
New Member
nima vaziri
Join Date: Aug 2011
Posts: 5
Rep Power: 14  |
Hi bearcat,
Check your equation with : O. M. Faltinsen, A numerical nonlinear method of sloshing in tanks with two- dimensional flow, J. Ship Research 22 (1978) |
|
|
|

|
|
|
|
|
#3 |
|
New Member
phillip
Join Date: Aug 2011
Posts: 7
Rep Power: 14  |
The reason it doesn't make any sense is that the fluid is modeled as being non-viscous. Viscosity would smooth out this behavior.
The model that you gave above looks like a cavity equation for quantum mechanics or electrodynamics. It's a very unrealistic model for fluid. It assumes that the fluid's motion can be decoupled into completely independent vibrational modes, but this just isn't the case in reality - there would be coupling due to viscosity. |
|
|
|

|
|
|
|
|
#4 |
|
New Member
phillip
Join Date: Aug 2011
Posts: 7
Rep Power: 14  |
I was just pondering this model a bit, and now I think its a completely ridiculous model!
First of all, the 'modes' don't make any sense - the sin(kx) are the shapes of the modes; however, these modes are always 0 at the sides of the container - this doesn't make any effen sense at all! There is no reason the liquid should be assumed to not be able to creep up the sides of the container. I don't think that even in the linear case that there is any reason for there to be a mode structure like this in the cavity. Also, each mode vibrates with its own frequency which gets infinitely fast as the series progresses - but this def would not happen - - - this model would tell you that if the water started out in a very fine wavy shape, it would ripple arbitrarily quickly. This is just silly. Probably a better way to model this simply is a superposition of 2 waves which move at some speed (dependent on their amplitude) and opposite directions get reflected at the boundaries. And so I'm not just saying a bunch of critical baloney, I derived a version of this for you; I may have made a mistake, I'm not taking the time to double check . . . Here, x is measured from either side of the container, L is the length of the container, and c is the speed of the wave (just set it however you like for now, figuring out what it should be will take a little more physics): Sum over all ODD n for n = 1 to infinity of: 8*tan(theta)*L*cos(n*pi*x/L)*cos(n*pi*c*t/L)/(pi*n)^2 that should do it - and it doesn't have a silly built in assumption where the waves components should all be zero at the sides of the container. The main difference between my formula and the one you posted is that I don't assume that the water can be analyzed in terms of wave shapes which would vibrate at different speeds; I just decomposed a triangle in that form and assumed the entire Wave moved at a single speed. I know this isn't realistic either really - I wonder - does this solution look any better to you?? |
|
|
|

|
|
|
|
|
#5 |
|
New Member
phillip
Join Date: Aug 2011
Posts: 7
Rep Power: 14  |
it looks ridiculous. (mine). Maybe if I set theta really tiny and let it move faster (my comp can't play the movie very fast) it'll look better . . .
|
|
|
|

|
|
|
|
|
#6 |
|
New Member
phillip
Join Date: Aug 2011
Posts: 7
Rep Power: 14  |
is not what I thought at all! I thought, stupidly, that they were measuring coordinates from the sides of the container. Their solution looks totally excellent! The reason it looks so wavy is because of the time dependences of each of the modes - they aren't integral multiples of one another, so they never intersect again after the initial flow begins.
Shows what I know, I think their solution is actually quite excellent looking! |
|
|
|

|
|
|
|
|
#7 |
|
New Member
phillip
Join Date: Aug 2011
Posts: 7
Rep Power: 14  |
Either way, I plotted yours too - its definitely unrealistically wobbly - but that's just because there's no damping from viscosity. However, the complicated time dependence makes something way more convincing than the one I came up with myself.
I modified your solution to accommodate an initial condition of splashing (a delta function velocity distribution right at the center at t = 0). Its the same as your solution except you drop the factor of n^2 in the denominator and any other constants of proportionality, and replace the spatial sine function with a cosine function. If you add up like 200 terms, it looks totally awesome. This is the end of my investigation - could you tell me where you found the derivation of that formula?? |
|
|
|

|
|
|
|
|
#8 | |
|
Member
|
Thank you for all the replies.
I first found it from "Standing wave induced by free liquid sloshing in rectangular tank", International Renewable Energy Congress, 2010. The author didn't tell the origin of this expression. X range is [-0.5*L, 0.5*L]. But it works okay for his validation. Reply one provided a paper. Though I don't have access to it as it's pretty old, I can find some other papers that cited it. It should be related to the excited sloshing motion, rather than the free sloshing here. Quote:
|
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Water subcooled boiling | Attesz | CFX | 7 | January 5, 2013 03:32 |
| sw for 2D free surface shallow water? | Rob Snel | Main CFD Forum | 7 | August 4, 2000 11:03 |
| gravitational force for free surface flow | Jongtae Kim | Main CFD Forum | 1 | July 2, 2000 11:57 |
| Any Body got a Free Surface Solution in FIDAP | Dr. Ahmed Hassaneen | Main CFD Forum | 2 | November 8, 1999 14:59 |
| Radial jet with free surface using FIDAP | Dr. Ahmed Hassaneen | Main CFD Forum | 0 | October 28, 1999 13:20 |