 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Rafal
Join Date: Apr 2012
Posts: 1
Rep Power: 0  |
Hello everyone!
I'm trying to make a program that uses finite element method (FEM) to transient heat transfer. I'm using Matlab and already have a meshing algorithm. I'm trying to understand how to go further. The best for me would be to understand a simple example. So I've made one – a simple cube. I've put everything in a *.pdf file to make everything clear by proper text format. I marked all my (5) questions in red. They are also numbered so you can write answers to "question no #". Everything else is written in pdf. Link to download: http://wyslijto.pl/plik/g66y5hcqtt - click in FEM [v0.1].pdf In shortcut: I don't understand solving a FEM heat transient problem. I try to make it in Matlab. I made a simple cube example, it's made from 6 tetrahedra. I'm looking for someone to help me with my problems by solving this example or showing me a text algorithm how to do this - step by step. I will be really grateful for any help.  Best regards, Reload. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Rami Ben-Zvi
Join Date: Mar 2009
Posts: 155
Rep Power: 17  |
Reload,
It's simple, and I'll just sketch the FEM procedure for the case in hand (conduction, transient solution). Let us write the equation (using tensor notation) as: 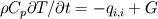 with 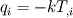 Assume T distribution within an element is 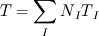 with 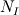 and and 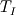 being the nodal shape functions and temperatures, and the sum is on the element nodes. being the nodal shape functions and temperatures, and the sum is on the element nodes.Now, apply Galerkin's method, i.e., integrate both hands multiplied by 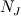 over the element volume. over the element volume.The LHS will be 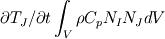 The RHS, after using intergation by parts and the Gauss theorem, yields 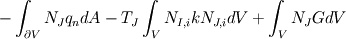 The first term on the RHS is the boundary normal flux, integrated over the element surface. Now sum over all the elements and assemble to get the global matrix equation 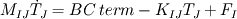 You have to specify appropriate initial conditions, the shape functions (apparently you used linear functions) and a time scheme (simple differencing will do). You also have to specify the boundary conditions. You may wish to choose G distribution (e.g., use the same shape function as for T), and - voila! That's the FEM in a nutshell. I hope I have clarified your doubts,
Rami Last edited by Rami; April 17, 2012 at 04:35. |
|
|
|

|
|
 |
| Tags |
| fem, heat flow |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Heat transfer problem at nucleate boiling | MrStuebb | FLUENT | 12 | March 14, 2017 13:31 |
| Natural Convection heat transfer problem | srinivasa | FLUENT | 21 | November 11, 2016 06:08 |
| simple heat transfer problem | openfoam1 | OpenFOAM | 2 | January 27, 2010 14:17 |
| Wall heat transfer coefficient (HTC) problem | Mohamed khamis | CFX | 1 | January 15, 2010 23:12 |
| How can I increase Heat Transfer at Domain Interf? | B.Simon | CFX | 3 | October 28, 2008 18:53 |