 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Vincent Leroy
Join Date: Jul 2012
Location: Rhode-Saint-Genèse, Belgium
Posts: 43
Rep Power: 14  |
Dear OpenFOAM users,
I solved a flow problem over and array of cylinders: https://www.dropbox.com/s/v5nz4mvx6user06/6-4_cell.png I would like to get the volume average of the velocity and pressure fields over a limited, moving volume (typically the size of a single cell, see the mask on the screenshot). The resulting field would be continuously defined over the entire domain, including in the cylinders. This is field volume averaging / spatial frequency filtering, in the sense of Whitaker (1999) and is somehow like the spatial averaging operation used for LES theory. Do you think it is possible to do this while solving the problem or as a post-processing operation? I didn't find a way to apply such a moving filter in Paraview or in the sample utility, and I don't know how to program this in a solver. Last edited by leroyv; February 18, 2014 at 12:25. Reason: added more precision |
|
|
|

|
|
|
|
|
#2 |
|
Member
Vincent Leroy
Join Date: Jul 2012
Location: Rhode-Saint-Genèse, Belgium
Posts: 43
Rep Power: 14  |
Additional (maybe simpler) question: How to export the fields to that kind format:
x y z Ux Uy Uz p with (x,y,z) coordinates on a cartesian grid. Just doing that would be sufficient, the computation of the average being possible as a post-processing operation. Last edited by leroyv; February 21, 2014 at 09:04. Reason: Removed quote |
|
|
|

|
|
|
|
|
#3 |
|
Member
Vincent Leroy
Join Date: Jul 2012
Location: Rhode-Saint-Genèse, Belgium
Posts: 43
Rep Power: 14  |
After a week of hacking (or so), I put together a solution. I forked simpleFoam and added this piece of code in it:
Code:
{
Info<<"Computing average velocity field\n" << endl;
// Constants
IOdictionary filterProperties(
IOobject(
"filterProperties",
runTime.system(),
mesh,
IOobject::MUST_READ,
IOobject::NO_WRITE
)
);
// This is AWFUL hacking
scalar filterRadius = dimensionedScalar(filterProperties.lookup("filterRadius")).value(),
filterXMin = dimensionedScalar(filterProperties.lookup("filterXMin")).value(),
filterXMax = dimensionedScalar(filterProperties.lookup("filterXMax")).value(),
filterYMin = dimensionedScalar(filterProperties.lookup("filterYMin")).value(),
filterYMax = dimensionedScalar(filterProperties.lookup("filterYMax")).value();
int nX = dimensionedScalar(filterProperties.lookup("nX")).value(),
nY = dimensionedScalar(filterProperties.lookup("nY")).value();
scalar hX = (filterXMax - filterXMin) / int(nX-1),
hY = (filterYMax - filterYMin) / int(nY-1);
const volVectorField & cellCenterField = mesh.C();
const DimensionedField<scalar, volMesh> & cellVolumeField = mesh.V();
// Variable initialization
scalar normInfty = 0.;
scalar filterCellVolume = 0.;
Vector<scalar> filterCenter(0.,0.,0.);
Vector<scalar> currentCellCenter(0., 0., 0.);
List<Vector<scalar> > filterCenterList;
List<Vector<scalar> > UBarList;
volScalarField filter(
IOobject(
"filter",
runTime.timeName(),
mesh,
IOobject::NO_READ,
IOobject::NO_WRITE
),
mesh,
dimensionedScalar("filter", dimensionSet(0,0,0,0,0,0,0), 0.)
);
// Build field center list
for ( int j = 0; j < nY; ++j )
{
for ( int i = 0; i < nX; ++i)
{
filterCenterList.append(
Vector<scalar>(
filterXMin + hX * int(i),
filterYMin + hY * int(j),
0.
)
);
}
}
UBarList.resize(filterCenterList.size());
// Loop over filter center coordinates
forAll(filterCenterList, iFilterCenterList)
{
// Define filter center
filterCenter = filterCenterList[iFilterCenterList];
//Info<< "filterCenter = " << filterCenter << endl;
// Set filter
forAll(cellCenterField, iCellCenterField)
{
currentCellCenter = cellCenterField[iCellCenterField];
normInfty = max( mag(currentCellCenter.x() - filterCenter.x()),
max( mag(currentCellCenter.y() - filterCenter.y()),
mag(currentCellCenter.z() - filterCenter.z()) ) );
filter[iCellCenterField] = (( normInfty <= filterRadius ) ? 1. : 0.);
}
// Compute filter cell volume
filterCellVolume = fvc::domainIntegrate(filter * cellVolumeField).value();
// Compute average velocity
UBarList[iFilterCenterList] = fvc::domainIntegrate(filter * cellVolumeField * U).value() / filterCellVolume;
//Info<< "UBar = " << UBarList[iFilterCenterList] << endl << endl;
} // Loop over filter center coordinates
// Output the UBar field to a custom-format ASCII file
// (please note that the call for sqrt is ambiguous due to the damn
// using namespace statement)
// TODO (low priority): modify output directory cleanly (current solution is hack)
// TODO (low priority): add progression indicator
fileName outputFile("postProcessing/UBar.csv");
Info<< "outputFile = " << outputFile << endl;
OFstream os(outputFile);
os << "\"x\",\"y\",\"z\",\"UBarX\",\"UBarY\",\"UBarZ\",\"UBarMag\"" << endl;
forAll(filterCenterList, iFilterCenterList)
{
os << filterCenterList[iFilterCenterList][0] << ","
<< filterCenterList[iFilterCenterList][1] << ","
<< filterCenterList[iFilterCenterList][2] << ","
<< UBarList[iFilterCenterList][0] << ","
<< UBarList[iFilterCenterList][1] << ","
<< UBarList[iFilterCenterList][2] << ","
<< Foam::sqrt( sqr(UBarList[iFilterCenterList][0])
+ sqr(UBarList[iFilterCenterList][1])
+ sqr(UBarList[iFilterCenterList][2])
)
<< endl;
if ( (iFilterCenterList+1)%nX == 0 ) os << endl; // Useful for gnuplot pm3d
}
}
Handling multiprocessor cases is critical, and I found the solution there: http://www.cfd-online.com/Forums/ope...ral-mag-u.html I believe there's a bottleneck at the filter setting operation, which is not parallelized. Last edited by leroyv; February 27, 2014 at 12:54. |
|
|
|

|
|
|
|
|
#4 |
|
Member
Vincent Leroy
Join Date: Jul 2012
Location: Rhode-Saint-Genèse, Belgium
Posts: 43
Rep Power: 14  |
Dear foamers,
Does anyone know if an LES filter wouldn't be suitable to do this? I can't exactly understand what the simpleFilter, laplaceFilter, and such, do. |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Sebastian Bomberg
Join Date: Aug 2012
Location: Munich, Germany
Posts: 12
Rep Power: 13  |
OK. I see this thread is rather old but still...
I implemented some explicit filtering/moving average, too. It works in parallel but takes ages. And edge effects are also an issue with this filtering stuff. So here's what I'm doing now: In k-space (wave number), the frequency response of a moving average filter (rectangular impulse response) is a sinc function: <phi> = sin(L/2*k)/(L/2*k) phi for a generic variable phi, filter length L and brackets <> denoting filtering. you can express this as an infinite series: sinc(L/2*k) = sum_n [L/2*(i*k)]^(2*n) /[(2*n+1)!] for n from zero to infinity. Note that (i*k)^2 is essentially the Laplacian. Now let's write this in a recursive manner: At iteration m <phi>_m = <phi>_(m-1) + (L/2)^2/[2*m*(2*m+1)] Laplacian[<phi>_(m-1)] This is basically the heat equation with a time-dependent diffusivity (tau is the numerical time step) d<phi>/dt = (L/2)^2/tau /[2t/tau*(2t/tau+1)] Laplacian[<phi>] Actually, from the series expansion we get Explicit Euler time integration which is numerically unstable unless Diffusion number is very small. Although it's mathematically not that sound, I just use implicit time integration here. Remember this is "pseudo time". You have to run this until some steady state at every real time step. But Laplace Equation is easy to solve and as the diffusivity decreases with time it should converge rather quickly. Edit: This derivation is for 1D. Physically it makes sense, I think. But I'd be glad if someone could comment on the multidimensional problem... Last edited by sebas; October 9, 2014 at 09:14. |
|
|
|

|
|
|
|
|
#6 |
|
Member
Vincent Leroy
Join Date: Jul 2012
Location: Rhode-Saint-Genèse, Belgium
Posts: 43
Rep Power: 14  |
Hi Sebastian,
This way of doing things seems quite elegant to me. However, there are a few things that remain unclear to me. I'm going to do a more detailed development of the calculus, using proper math notations for more clarity. That will help me explain where the things I don't understand are. We start with a given field  we want to get the average of using what I'll call the we want to get the average of using what I'll call the 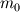 top-hat filter of width top-hat filter of width 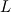 : :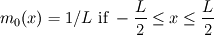 and 0 otherwise. Note that this filter is the first of a family of recursively defined filters that have interesting properties regarding control of the regularity of the resulting averaged field (see Angeli et al., 2013). We get the average field 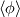 by applying the by applying the 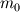 filter using a convolution operator. filter using a convolution operator. 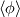 's expression in 's expression in  is: is: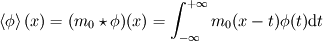 Now, we go to the phase space by applying the Fourier transform operator 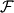 : : = \mathcal{F}[m_0](k) \ \mathcal{F}[\phi](k) \mathcal{F}[\left< \phi \right>](k) = \mathcal{F}[m_0](k) \ \mathcal{F}[\phi](k)](/Forums/vbLatex/img/90510811de2ae93eb8c8631fef9af76f-1.gif) where 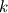 is the wave vector. is the wave vector.The only problem-independant thing we have here is the Fourier transform of the filter. As you mentioned, the Fourier transform of 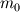 is a sinc: is a sinc: = \mathrm{sinc}\left(\frac{kL}{2}\right) \mathcal{F}[m_0](k) = \mathrm{sinc}\left(\frac{kL}{2}\right)](/Forums/vbLatex/img/1b1b2c3ae04863001bc60663ff9072b8-1.gif) and its Taylor series expansion is 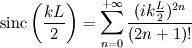 This gives us the following expression for ![\mathcal{F}[\left< \phi \right>] \mathcal{F}[\left< \phi \right>]](/Forums/vbLatex/img/96bd1328f59ce6d9c8304797308afab6-1.gif) : : = \sum_{n = 0}^{+\infty} \left( \frac{(ik\frac{L}{2})^{2n}}{(2n+1)!} \mathcal{F}[\phi](k) \right) = \lim_{n \rightarrow +\infty} S_n \mathcal{F}[\left< \phi \right>](k) = \sum_{n = 0}^{+\infty} \left( \frac{(ik\frac{L}{2})^{2n}}{(2n+1)!} \mathcal{F}[\phi](k) \right) = \lim_{n \rightarrow +\infty} S_n](/Forums/vbLatex/img/eb32f871e69d99d337a93bd658595e11-1.gif) where  S_n = \sum_{m=0}^n \frac{(ik\frac{L}{2})^{2n}}{(2n+1)!} \mathcal{F}[\phi](k)](/Forums/vbLatex/img/f8c88e3a9a6d4263d39fd51dc9fd0cc4-1.gif) For there, we can move to a recursive definition of the 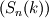 sequence: sequence: S_n(k) = S_{n-1}(k) + \frac{(ik\frac{L}{2})^{2n}}{(2n+1)!} \mathcal{F}[\phi](k)](/Forums/vbLatex/img/fe83a854c629594a7fdd23c1e2364d80-1.gif) with the initial condition  S_0(k) = \mathcal{F}[\phi](k)](/Forums/vbLatex/img/3d415d2fc983d07ba15b76f3e262b008-1.gif) Finding the limit of the 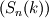 sequence would clearly give us sequence would clearly give us ![\mathcal{F}[\left< \phi \right>] \mathcal{F}[\left< \phi \right>]](/Forums/vbLatex/img/96bd1328f59ce6d9c8304797308afab6-1.gif) , indeed. What I don't understand at this point is how you proceed to the laplacian-based formulation you provide: the , indeed. What I don't understand at this point is how you proceed to the laplacian-based formulation you provide: the 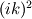 product meaning "apply laplacian" only works if you go back to the real space, in which the recursive definition doesn't work. Plus, we don't have product meaning "apply laplacian" only works if you go back to the real space, in which the recursive definition doesn't work. Plus, we don't have 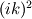 in the recursive definition; only in the recursive definition; only 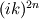 , a lot less convenient. Did I miss something? , a lot less convenient. Did I miss something?I've also been trying to write this for a 2D problem, but I couldn't figure out how to get to a recursive expression for the Taylor series terms, mostly because the Fourier transform of the 2D 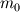 filter is a product of two Taylor series (I'm not a good mathematician). filter is a product of two Taylor series (I'm not a good mathematician).
Last edited by leroyv; October 9, 2014 at 11:02. Reason: grammar |
|
|
|

|
|
 |
| Tags |
| filter, large eddy simulation, les, openfoam, volume averaging |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [Other] mesh airfoil NACA0012 | anand_30 | OpenFOAM Meshing & Mesh Conversion | 13 | March 7, 2022 17:22 |
| [snappyHexMesh] No layers in a small gap | bobburnquist | OpenFOAM Meshing & Mesh Conversion | 6 | August 26, 2015 09:38 |
| draw any scalar vs. cell volume | wersoe | OpenFOAM Post-Processing | 0 | April 3, 2012 03:52 |
| negative cell volume in dynamic mesh | WU zhonghua | FLUENT | 0 | July 28, 2004 10:04 |
| calculate cell volume, center...? | Paul | Main CFD Forum | 5 | June 21, 2003 12:55 |