 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Vincent Leroy
Join Date: Jul 2012
Location: Rhode-Saint-Genèse, Belgium
Posts: 43
Rep Power: 14  |
Dear OpenFOAM users,
I am developing a solver for a 1D application. I started with laplacianFoam as a base, and at some point, I had to introduce a source term which is a combination of laplacian(DT, T) in some cells and and some other computations in the others (impossible to use partitioning into regions because the cells concerned by the special computations change dynamically). Since I could not mix implicit and explicit terms, I decided to go fully explicit and used fvc::laplacian(DT, T). This resulted in a crash of the solver. On the forum, I saw that people having that problem usually have it solved by simply changing the numerical scheme; however, in the case of that 1D example, it does not seem to make a difference. I investigated using a minimal working example attached to this post. It is made of:
Question: Does someone have an idea of what is happening? PS: In case that would be of any help, I should also mention that in the practical example I am dealing with (not the MWE), the source term wiggles very oddly and explodes when going in the direction of the "hot" wall. I attached a screenshot of postprocessed data: in blue is the initial source term (non-zero, but small intensity compared to the green curve) and in green is the source term after the first time step. |
|
|
|

|
|
|
|
|
#2 |
|
Super Moderator
Tobias Holzmann
Join Date: Oct 2010
Location: Tussenhausen
Posts: 2,708
Blog Entries: 6
Rep Power: 51    |
Dear Vincent,
first of all, thank you for investigating into your first post and providing all the necessary information that we need to help you. There is only one information missing (the version of FOAM you are using but I guess it is 2.3.1). It is very seldom that we got these informations within the first post. Cause of your problem I checked your solver and especially your domain. I hope you know the differences between explicit and implicit. The problem you are solving is a parabolic problem and here you have a strict criteria that has to be fulfilled. It is the Fourier Number. If you have 1D problems and you solve just the laplace equation with an explicit scheme, you are limited to Fo = 0.5. 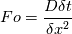 and hence 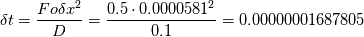 Or if we check the Fourier Number we would get with your settings: 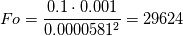 The residual demonstrate this too. Hence, you know why explicit is always a bad choice. If you reduce your time step below 1e-7 your solver works based on the theory above. That's all.
__________________
Keep foaming, Tobias Holzmann |
|
|
|

|
|
|
|
|
#3 |
|
Member
Vincent Leroy
Join Date: Jul 2012
Location: Rhode-Saint-Genèse, Belgium
Posts: 43
Rep Power: 14  |
Hi Tobias,
Thank you very much for this thorough answer. Sometimes, I get lost in the complicated stuff and even forget about the most elementary things. Coming back to my original problem: my conservation equation is 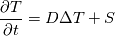 where 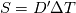 in some regions and is gotten from another solver elsewhere. How come the laplacian part of in some regions and is gotten from another solver elsewhere. How come the laplacian part of 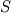 affects the stability of the problem? Does this mean that not satisfying the stability criterion results in practice in (very) wrong values of the explicitly evaluated laplacian operator? affects the stability of the problem? Does this mean that not satisfying the stability criterion results in practice in (very) wrong values of the explicitly evaluated laplacian operator?
|
|
|
|

|
|
 |
| Tags |
| explicit, laplacian operator |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [Other] engineFoam new mesh problem | ayhan515 | OpenFOAM Meshing & Mesh Conversion | 5 | August 10, 2015 08:45 |
| UDF compiling problem | Wouter | Fluent UDF and Scheme Programming | 6 | June 6, 2012 04:43 |
| Gambit - meshing over airfoil wrapping (?) problem | JFDC | FLUENT | 1 | July 11, 2011 05:59 |
| natural convection problem for a CHT problem | Se-Hee | CFX | 2 | June 10, 2007 06:29 |
| Adiabatic and Rotating wall (Convection problem) | ParodDav | CFX | 5 | April 29, 2007 19:13 |