 |
|
|
[Sponsors] | |||||
TEqn implementation in icoReactingMultiphaseInterFoam |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Gowthaman Parivendhan
Join Date: Aug 2019
Location: Dublin, Ireland
Posts: 3
Rep Power: 6  |
Hi Foamers,
I have a basic question on implementation of temperature equation in one of the solvers in OF v1806. I was going through the TEqn.H file of icoReactingMultiphaseInterFoam in OF and found the following implementation: Code:
fvScalarMatrix TEqn
(
fvm::ddt(rhoCp, T)
+ fvm::div(rhoCpPhi, T, "div(phi,T)")
- fvm::Sp(fvc::ddt(rhoCp) + fvc::div(rhoCpPhi), T)
- fvm::laplacian(kappaEff, T, "laplacian(kappa,T)")
==
fluid.heatTransfer(T)
+ radiation->ST(T)
+ fvOptions(rhoCp, T)
);
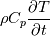 + + 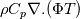 - - 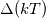 If that is the case, then why are density and Cp has taken out as constant? Shouldn't the volume of fluid averaged rhoCp depend on both time and space in a multiphase system? Please let me know if I'm missing something here as I'm quite new to heat transfer modelling. Many thanks, Gowthaman |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Corbin G
Join Date: Oct 2022
Location: Midwest, USA
Posts: 11
Rep Power: 3  |
Hi Gowthaman,
I think you are correct. At least for the transient term we can use the product rule to expand: 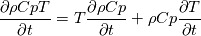 Using algebra to rearrange we have the below equation. The right hand side corresponds, in so far as I can tell, to what is implemented in icoReactingMultiphaseInterFoam TEqn.H. Therefore, effectively the LHS is being calculated. 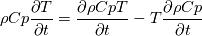 Now, why code the right hand side instead of just putting 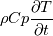 directly? I have a theory: fvm::ddt(rhoCp, T) makes an fvScalarMatrix data type. OpenFOAM, in my experience, does not allow the multiplication of volScalarField by fvScalarMatrix or it will give error at compilation. That is to say, if we had rhoCp stored as volScalarField, rhoCp*fvm::ddt(T) would give volScalarField*fvScalarMatrix compilation error. directly? I have a theory: fvm::ddt(rhoCp, T) makes an fvScalarMatrix data type. OpenFOAM, in my experience, does not allow the multiplication of volScalarField by fvScalarMatrix or it will give error at compilation. That is to say, if we had rhoCp stored as volScalarField, rhoCp*fvm::ddt(T) would give volScalarField*fvScalarMatrix compilation error. Fauster has documented this volScalarField*fvScalarMatrix compilation error, but no one has responded a way to get around it: How to multiply volScalarField and fvScalarMatrix ? EDIT: Thank you to newGuyAtCFD for pointing out my oversight. Please regard my aforementioned theory as incorrect. volScalarField*fvScalarMatrix IS possible. But, fvScalarMatrix*volScalarField gives compilation error: Code:
volScalarField rhoCp1 = rho1*alpha1*mixture.thermo1().Cp() + rho2*alpha2*mixture.thermo2().Cp(); fvScalarMatrix eEqn ( rhoCp1*fvm::ddt(T) // compiles OK! //fvm::ddt(T)*rhoCp1 // gives compilation error! == fvOptions(rhoCp1, T) ); Last edited by CorbinMG; December 14, 2022 at 11:34. |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Join Date: Sep 2022
Posts: 18
Rep Power: 3  |
Quote:
To my understanding the above code should represent: ![\frac{\partial \left(\rho C_p T\right)}{\partial t} + \nabla \cdot (\rho C_p \vec{v} T) - T\left [ \frac{\partial \left(\rho C_p\right)}{\partial t} + \nabla \cdot \left(\rho C_p \vec{v} \right)\right ] - \nabla \cdot \left( k_{eff} \nabla T\right) = S_T \frac{\partial \left(\rho C_p T\right)}{\partial t} + \nabla \cdot (\rho C_p \vec{v} T) - T\left [ \frac{\partial \left(\rho C_p\right)}{\partial t} + \nabla \cdot \left(\rho C_p \vec{v} \right)\right ] - \nabla \cdot \left( k_{eff} \nabla T\right) = S_T](/Forums/vbLatex/img/482ed71a59ab62abdf41841f7f28e6b4-1.gif) Where everything is inside the parenthesis. Please correct me if I am wrong. Also, multiplying a volScalarField with a matrix is possible and defined on line 2816-2826 of fvMatrix.C Code:
template<class Type>
Foam::tmp<Foam::fvMatrix<Type>> Foam::operator*
(
const volScalarField::Internal& dsf,
const tmp<fvMatrix<Type>>& tA
)
{
tmp<fvMatrix<Type>> tC(tA.ptr());
tC.ref() *= dsf;
return tC;
}
Last edited by newGuyAtCFD; December 6, 2022 at 05:54. |
|
|
|

|
|
|
|
|
#4 | |
|
Member
Join Date: Jan 2022
Location: Germany
Posts: 72
Rep Power: 4  |
Quote:
I agree with you, but corrected the T into the derivatives. The orginial equation should look like this with the mentioned substitutions of the reformulated differentials. I mean this should be equal 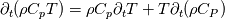 same for the divergence term. Then it follows: 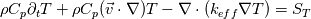 Which is nothing else than:  My guess is that inserting of the reformulated differentials was done either because of discretization reasons or because of the interphase properties. |
||
|
|

|
||
|
|
|
#5 |
|
New Member
S Abrahams
Join Date: Mar 2022
Location: UK
Posts: 14
Rep Power: 4  |
Hi everyone,
I wonder if anyone can help me with a follow-up question please? In compressibleInterFoam in OF9, the TEqn is formulated as Code:
fvm::ddt(rho, T) + fvm::div(rhoPhi, T) - fvm::Sp(contErr, T)
- fvm::laplacian(turbulence.alphaEff(), T)
+ (
fvc::div(fvc::absolute(phi, U), p)()() // - contErr/rho*p
+ (fvc::ddt(rho, K) + fvc::div(rhoPhi, K))()()
- (U()&(fvModels.source(rho, U)&U)()) - contErr*K
)
*(
alpha1()/mixture.thermo1().Cv()()
+ alpha2()/mixture.thermo2().Cv()()
)
==
fvModels.source(rho, T)
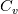 is used instead of is used instead of 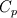 but I believe it should still be inside the derivatives since the averaged but I believe it should still be inside the derivatives since the averaged 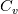 can vary in time and space. can vary in time and space. I believe the TEqn should be equivalent to 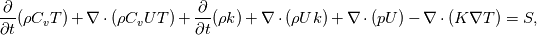 but the formulation above seems to be equivalent to ![\frac{C_{1}C_{2}}{{\alpha_1 C_{2}+\alpha_2 C_{1}}} \left[\frac{\partial}{\partial t}(\rho T)+\nabla\cdot(\rho U T) \right]+ \frac{\partial}{\partial t}(\rho k)+\nabla\cdot(\rho U k)+\nabla \cdot (pU)-\nabla\cdot (K \nabla T)=S. \frac{C_{1}C_{2}}{{\alpha_1 C_{2}+\alpha_2 C_{1}}} \left[\frac{\partial}{\partial t}(\rho T)+\nabla\cdot(\rho U T) \right]+ \frac{\partial}{\partial t}(\rho k)+\nabla\cdot(\rho U k)+\nabla \cdot (pU)-\nabla\cdot (K \nabla T)=S.](/Forums/vbLatex/img/07201cb49aceb151874cd41d86b52f3a-1.gif) Can anyone help me to understand how 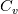 has been taken out in this way? has been taken out in this way?Many thanks, SAbrahams 
Last edited by sabrahams; August 9, 2023 at 13:16. Reason: spelling |
|
|
|

|
|
 |
| Tags |
| heat and mass transfer, openfoam 1806, teqn, vof method |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Radiation Models in General and the P1 implementation | Tobi | OpenFOAM Running, Solving & CFD | 8 | September 21, 2021 05:59 |
| Issues in FGM combustion model implementation | Lisandro Maders | OpenFOAM Programming & Development | 15 | April 22, 2020 19:18 |
| Explicit source term implementation | wvn | OpenFOAM Programming & Development | 0 | November 14, 2018 11:31 |
| Implementation issues of fvSchemes / laplacianScheme, in particular gaussLaplacianSch | thomek | OpenFOAM Programming & Development | 0 | October 18, 2010 05:10 |
| Please explain the implementation of species transport Eqn in reactingFoam | kallipygian | OpenFOAM Running, Solving & CFD | 0 | October 13, 2008 07:29 |