 |
|
|
[Sponsors] | |||||
|
|
|
#1 | |||||
|
Senior Member
Illya Shevchuk
Join Date: Aug 2009
Location: Darmstadt, Germany
Posts: 176
Rep Power: 16  |
Hi Foamers,
in compressible solvers continuity is solved for density: Code:
solve(fvm::ddt(rho) + fvc::div(phi)); But how can I solve continuity for velocity? I already tried to solve: Code:
fvScalarMatrix UEqn
(
fvc::ddt(rho)
+ fvm::div(rho,U)
);
Quote:
Code:
fvScalarMatrix UEqn
{
fvc::ddt(rho)
+ fvm::div(fvc::interpolate(rho),U)
}
Quote:
Code:
fvScalarMatrix UEqn
(
fvc::ddt(rho)
+ fvm::div(rho,phi)
);
Quote:
Code:
fvScalarMatrix UEqn
(
fvc::ddt(rho)
+ fvm::div(fvc::interpolate(rho),phi)
);
Quote:
Code:
fvVectorMatrix UEqn
(
fvc::ddt(rho)
+ fvm::div(fvc::interpolate(rho),U)
);
Quote:
 Best, |
||||||
|
|

|
||||||
|
|
|
#2 |
|
Senior Member
Illya Shevchuk
Join Date: Aug 2009
Location: Darmstadt, Germany
Posts: 176
Rep Power: 16  |
I'm a little bit confused:
thus I am looking for a volVectorField U, my system of equations should be fvVectorMatrix. But the continuity equation is a scalar one and the term div(rho,U) is a scalar field. So for each cell I have 3x unknowns but only 1x equation, right? On the other hand, it should be possible to obtain continuity-based velocities in 1D. How can it be implemented, if I want to start with an 1D-case? Furthermore, if I prescribe the temporal density change for each cell and provide velocities for every boundary cell but one, only one velocity field is possible, that satisfies these conditions, am I right? So how this velocity field can be obtained? |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Felix L.
Join Date: Feb 2010
Location: Hamburg
Posts: 165
Rep Power: 18  |
Hello, linch,
you are right, the continuity equation is a scalar equation so it can only be solved for a single unknown scalar. This may be the density (which would be the easy way) or any velocity component. Still the continuity equation is one equation, so even if you know the temporal variation and the mass fluxes at the boundaries, there will be aribitrary velocity fields which satisfy the continuity equation. Just imagine the following setup: A rectangular, twodimensional domain. The continuity equation is 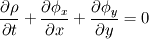 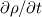 shall be known throughout the domain and at every boundary face it shall be shall be known throughout the domain and at every boundary face it shall be 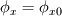 and and 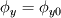 . .Out of the box there come two different velocity fields to my mind which satisfiy the continuity equation: either one, where 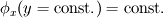 , thus , thus 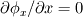 or another, where or another, where 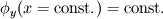 , thus , thus 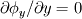 . .The partial derivative of the other mass flux component is then equal to 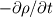 So it's not possible to obtain a velocity field from the continuity equation without any additional information. In 1D it should be possible, though, as long as the variation of density is known. Just treat the velocity component as a scalar. Greetings, Felix Last edited by FelixL; June 27, 2011 at 15:02. |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Illya Shevchuk
Join Date: Aug 2009
Location: Darmstadt, Germany
Posts: 176
Rep Power: 16  |
Thank you Felix,
to treat the velocity as scalar is a great idea! |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Illya Shevchuk
Join Date: Aug 2009
Location: Darmstadt, Germany
Posts: 176
Rep Power: 16  |
One more question Felix,
which boundary condition would you suggest for velocity for the open end, since no boundary condition is needed? In 1D, one velocity and known density changes are fully sufficient. Otherwise the system of equations is overdetermined. Is there any "no condition" boundary in OF? |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Felix L.
Join Date: Feb 2010
Location: Hamburg
Posts: 165
Rep Power: 18  |
I was thinking about it for a bit and I don't think it would make sense doing this with OpenFOAM.
If you know 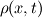 and you want to solve for and you want to solve for 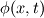 , the 1D continuity equation simply becomes an ODE. So unless you don't have any other PDEs coupled with the continuity equation, it would make much more sense solving this equation using an ODE solver and not with finite volume methods. , the 1D continuity equation simply becomes an ODE. So unless you don't have any other PDEs coupled with the continuity equation, it would make much more sense solving this equation using an ODE solver and not with finite volume methods.What's your intention, anyway, if I may ask? Greetings, Felix. |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Illya Shevchuk
Join Date: Aug 2009
Location: Darmstadt, Germany
Posts: 176
Rep Power: 16  |
Thanks again Felix,
Well, I also have PDEs for enthalpy and components to solve. And the intention is to test, if diffusive heat and mass transfer as well as evaporation models are working in 1D, before adding the momentum equation. That's the background. |
|
|
|

|
|
 |
| Tags |
| continuity equation, velocity field |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Solve Flow or VOF simultaneously ? | Ramsey | FLUENT | 1 | February 16, 2011 13:16 |
| Linearized NS euqations: how to solve them?(problem with Matrix operations..) | matteoL | OpenFOAM Running, Solving & CFD | 0 | November 18, 2009 06:58 |
| Solve for two or more "Temperatures" | Rui | CFX | 12 | September 9, 2008 21:58 |
| How FVM will solve shock problem? | michael | Main CFD Forum | 4 | June 13, 2007 09:07 |
| How to solve another continuum and momentum eqn? | west_wing | FLUENT | 0 | August 25, 2003 10:00 |