 |
|
|
[Sponsors] | |||||
k-epsilon implementation? (including volScalarField G) |
 11Likes
11Likes
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Oskar
Join Date: Nov 2015
Location: Poland
Posts: 184
Rep Power: 10  |
Dear All.
I'm using: engineFoam (xiFoam), openfoam 2.2.1. I'm trying to understand k-epsilon turbulence model in openFoam but I can't get through those k and epsilon equations. Let's focus on k equation: Code:
tmp<fvScalarMatrix> kEqn
(
fvm::ddt(rho_, k_)
+ fvm::div(phi_, k_)
- fvm::laplacian(DkEff(), k_)
==
G
- fvm::SuSp((2.0/3.0)*rho_*divU, k_)
- fvm::Sp(rho_*epsilon_/k_, k_)
);
![\frac{\partial\rho k}{\partial t}+\frac{\partial}{\partial x_i}(\rho V_i k) = \frac{\partial}{\partial x_j}[(\mu+\frac{\mu_{turb}}{\sigma_k})\frac{\partial k}{\partial x_j}]+\mu_{turb} (\sqrt{2S_{ij}S_{ij}})^2-\rho\epsilon \frac{\partial\rho k}{\partial t}+\frac{\partial}{\partial x_i}(\rho V_i k) = \frac{\partial}{\partial x_j}[(\mu+\frac{\mu_{turb}}{\sigma_k})\frac{\partial k}{\partial x_j}]+\mu_{turb} (\sqrt{2S_{ij}S_{ij}})^2-\rho\epsilon](/Forums/vbLatex/img/5394ae8e3467f4c7dbc72269f59cf26b-1.gif) If that's true, then: fvm::ddt(rho_, k_) = 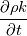 fvm::div(phi_, k_) = 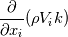 fvm::laplacian(DkEff(), k_) = ![\frac{\partial}{\partial x_j}[(\mu+\frac{\mu_{turb}}{\sigma_k})\frac{\partial k}{\partial x_j}] \frac{\partial}{\partial x_j}[(\mu+\frac{\mu_{turb}}{\sigma_k})\frac{\partial k}{\partial x_j}]](/Forums/vbLatex/img/47445623284e6add6becb902df18fadd-1.gif) fvm::Sp(rho_*epsilon_/k_, k_) = 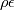 Probably: - fvm::SuSp((2.0/3.0)*rho_*divU, k_) = 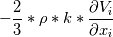 and maybe this term is to remove trace but as long as I cant understand G, I can't go any further. Definition of G is Code:
volScalarField G(GName(), mut_*(tgradU() && dev(twoSymm(tgradU())))); I can't figure out how: G - fvm::SuSp((2.0/3.0)*rho_*divU, k_) is equal to  If someone can correct me or lead me to correct answer it would be great. Greetings to all. |
|
|
|

|
|
|
|
|
#2 |
|
Member
Darko Radenkovic
Join Date: Oct 2015
Posts: 38
Rep Power: 10  |
Have a look here (page 123, at the top)
http://www.tfd.chalmers.se/~lada/pos...-modelling.pdf About G: You need volScalarField to enter k equation. Regards, Darko |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Oskar
Join Date: Nov 2015
Location: Poland
Posts: 184
Rep Power: 10  |
Hello. Thank You for this pdf but I can't find full solution (exact implementation formula).
According to my further research k-epsilon turbulent model is based on this report: "k-epsilon equation for compressible reciprocating engine flows", Journal of Energy, Vol. 7, No. 4 (1983), pp. 345-353. Unfortunately it is not free. |
|
|
|

|
|
|
|
|
#4 |
|
Member
Darko Radenkovic
Join Date: Oct 2015
Posts: 38
Rep Power: 10  |
Hello.
Here is your paper. https://www.dropbox.com/s/iwnvw5om0b...48086.pdf?dl=0 About your first post, in exact k equation (have look here) https://en.wikipedia.org/wiki/Turbulence_kinetic_energy find production term. Insert Bussinesk assumption  in that production term and you will get terms that you need. In the case of incompressible flow, 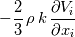 is equal to zero. Best regards, Darko |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Oskar
Join Date: Nov 2015
Location: Poland
Posts: 184
Rep Power: 10  |
Thank You once again, dear Darko. That 2nd report is very useful for me (eg. C_3 constant).
I'm really sorry but it still isn't clear for me. I have done what you said. The production term:  After applying Boussinesq Eddy Viscosity: 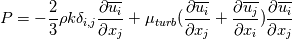 Removing delta Kronecker 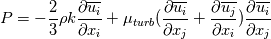 First term in openfoam: - fvm::SuSp((2.0/3.0)*rho_*divU, k_) = 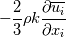 But I still don't understand how G = mut_*(tgradU() && dev(twoSymm(tgradU()))) = 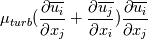 tgradU is temporary field of gradient U tgradU = 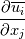 twoSymm(tgradU) returns 2*symmetric part of a tensor so: twoSymm(tgradU) = 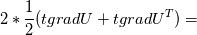  (Am I right here? Im pretty sure but...) (Am I right here? Im pretty sure but...)dev(twoSymm(tgradU())) - this one returns only deviatoric component of tensor tgradU dev(twoSymm(tgradU())) = 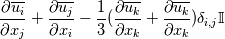 dev(twoSymm(tgradU())) = 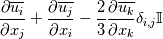 Is that right? Is that right?And at last: tgradU() && dev(twoSymm(tgradU())) means "double inner product" and it hard to understand. Definition of double inner product for two 2nd rank tensors: 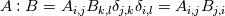 tgradU() && dev(twoSymm(tgradU())) = ![[\frac{\partial \overline{u_i}}{\partial x_j}] : [\frac{\partial \overline{u_l}}{\partial x_k}+\frac{\partial \overline{u_k}}{\partial x_l} - \frac{2}{3}\frac{\partial \overline{u_m}}{\partial x_m}\delta_{k,l} \mathbb{I}] [\frac{\partial \overline{u_i}}{\partial x_j}] : [\frac{\partial \overline{u_l}}{\partial x_k}+\frac{\partial \overline{u_k}}{\partial x_l} - \frac{2}{3}\frac{\partial \overline{u_m}}{\partial x_m}\delta_{k,l} \mathbb{I}]](/Forums/vbLatex/img/2d5c1381256fa604b0f6cd6a249132e3-1.gif) And I have no idea what to do now. Last edited by sheaker; August 25, 2016 at 17:18. |
|
|
|

|
|
|
|
|
#6 |
|
Member
Darko Radenkovic
Join Date: Oct 2015
Posts: 38
Rep Power: 10  |
Book at this link has very good introduction part about tensors
https://www.dropbox.com/s/72rz5760b3...ou%29.pdf?dl=0 Sooner or later, you will have to learn it, so it is better to start now. Pay attention to eq. 1.76, it will make things easier for you many times. If we use (1.148) from above book, it follows: tgradU() && dev(twoSymm(tgradU())) = ![\mu_t\,{\left({\mathbf{D} + \mathbf{\Omega}}\right)}:\left[2\mathbf{D} - \frac{2}{3}(tr \mathbf{D})\mathbf{I})\right] = \mu_t\left(2\mathbf{D}:\mathbf{D} - \frac{2}{3} (tr{\mathbf{D})^2}\right] \mu_t\,{\left({\mathbf{D} + \mathbf{\Omega}}\right)}:\left[2\mathbf{D} - \frac{2}{3}(tr \mathbf{D})\mathbf{I})\right] = \mu_t\left(2\mathbf{D}:\mathbf{D} - \frac{2}{3} (tr{\mathbf{D})^2}\right]](/Forums/vbLatex/img/cd688cc1ff9aad933542ab7e2f2c0b2a-1.gif) Last term is equal to zero when flow is incompressible. It has been utilized that product of symmetric and asymmetric tensor is zero. Regards, Darko |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Oskar
Join Date: Nov 2015
Location: Poland
Posts: 184
Rep Power: 10  |
Dear Darko. Thank You for a lot of patience to me.
I forgot about splitting gradU into symmetric and antisymmetric parts. I understand that: (tgradU() && dev(twoSymm(tgradU())) = ![{\left({\mathbf{D} + \mathbf{\Omega}}\right)}:\left[2\mathbf{D} - \frac{2}{3}(tr \mathbf{D})\mathbf{I}\right] = \left[2\mathbf{D}:\mathbf{D} - \frac{2}{3} (tr{\mathbf{D})^2}\right] {\left({\mathbf{D} + \mathbf{\Omega}}\right)}:\left[2\mathbf{D} - \frac{2}{3}(tr \mathbf{D})\mathbf{I}\right] = \left[2\mathbf{D}:\mathbf{D} - \frac{2}{3} (tr{\mathbf{D})^2}\right]](/Forums/vbLatex/img/8917ec9ed30cabba14706139ac587271-1.gif) According to previous hints: ![\left[{2\mathbf{D}:\mathbf{D} - \frac{2}{3} \left({tr{\mathbf{D}}}\right)^2}\right] \left[{2\mathbf{D}:\mathbf{D} - \frac{2}{3} \left({tr{\mathbf{D}}}\right)^2}\right]](/Forums/vbLatex/img/6d45fc9aa524fd7e1a156f963071fa58-1.gif) should be equal to should be equal to  And I'm not sure about that. The first one is a scalar and it looks correct but I can't transform it to that second form. Darko, wish You best! Last edited by sheaker; August 27, 2016 at 04:32. |
|
|
|

|
|
|
|
|
#8 |
|
Member
Darko Radenkovic
Join Date: Oct 2015
Posts: 38
Rep Power: 10  |
I wasn't clear enough.
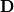 is rate of strain tensor and from the above mentioned link from Chalmers, page 123, you can see that is rate of strain tensor and from the above mentioned link from Chalmers, page 123, you can see that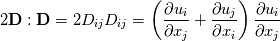 Term 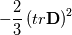 is not in your starting equation. is not in your starting equation.When I think better from the very beginning we used assumption of incompressible flow through Bussinesq assumption - in the case of compressible flow, Bussinesq assumption is 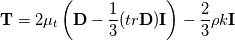 If you again insert Bussinesq assumption into production term of TKE, this forgotten term explains existence of 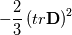 in Openfoam implementation of k-epsilon. in Openfoam implementation of k-epsilon. This agrees well with k equation of http://turbmodels.larc.nasa.gov/ke-chien.html Of course, in incompressible flow trace of rate of strain tensor is zero. Regards, Darko |
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
Oskar
Join Date: Nov 2015
Location: Poland
Posts: 184
Rep Power: 10  |
||
|
|

|
|
|
|
|
#10 |
|
Member
Darko Radenkovic
Join Date: Oct 2015
Posts: 38
Rep Power: 10  |
Couple hours ago I verified this on link in my above post (but now, at the moment of this writing, above link doesn't work).
If you check eq. (24) and eq. (37) from paper "k-e Equation for Compressible Reciprocating Engine Flows", 1983, I believe you will see that is it. Regards, Darko |
|
|
|

|
|
|
|
|
#11 |
|
Member
Sami
Join Date: Nov 2012
Location: Cap Town, South Africa
Posts: 87
Rep Power: 13  |
Hello all,
Thank you for this very useful discussion. I'm using multiphaseEulerFoam (OFv4) to perform simulation of two-phase (gas dispersed in liquid) dispersed flow. To model turbulence, I used the k-epsilon model. The code has a little bit changed in version 4 (https://github.com/OpenFOAM/OpenFOAM...lon/kEpsilon.C) compared to what you shared in last posts. In OFv4, we have source terms "kSource()" and "epsilonSource()". My understanding is that they are used for bubble induced turbulence in the case of two-phase dispersed flow. Do you know how they are implemented and what is their exact definition? Thank you. mhrz |
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
Jianrui Zeng
Join Date: May 2018
Location: China
Posts: 157
Rep Power: 8  |
I am also interested in kSource()and epsilonSource(). What is its function and meaning?
|
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
Joachim Herb
Join Date: Sep 2010
Posts: 650
Rep Power: 21  |
They are used to modify the turbulence model, e.g. for buoyancy effects. See https://github.com/OpenFOAM/OpenFOAM...uoyantKEpsilon
This turbulence model inherits from the basic compressible k-epsilon turbulence model and overwrites those methods to implement the effect of buoyancy on turbulence. |
|
|
|

|
|
|
|
|
#14 | |
|
New Member
Sourav Hossain
Join Date: Mar 2019
Posts: 25
Rep Power: 7  |
Quote:
|
||
|
|

|
||
|
|
|
#15 |
|
New Member
Sourav Hossain
Join Date: Mar 2019
Posts: 25
Rep Power: 7  |
Dear sir, Could you please share the paper and the book shared by Darko Radenkovi? The link is broken.
|
|
|
|

|
|
|
|
|
#16 |
|
New Member
Join Date: Jul 2017
Posts: 14
Rep Power: 9  |
Dear Sheaker
Do you have any Idea about G? Here we have tmp<fvScalarMatrix> kEqn ( fvm::ddt(alpha, rho, k_) + fvm::div(alphaRhoPhi, k_) - fvm::laplacian(alpha*rho*DkEff(), k_) == alpha*rho*G - fvm::SuSp((2.0/3.0)*alpha*rho*divU, k_) - fvm::Sp(Ce(D, KK)*alpha*rho*sqrt(k_)/this->delta(), k_) + kSource() + fvModels.source(alpha, rho, k_) ); I have understood the term - fvm::SuSp((2.0/3.0)*alpha*rho*divU, k_) but still this one is unclear: alpha*rho*G |
|
|
|

|
|
|
|
|
#17 | |
|
New Member
Join Date: Jul 2017
Posts: 14
Rep Power: 9  |
Quote:
Do you have any Idea about G? Here we have tmp<fvScalarMatrix> kEqn ( fvm::ddt(alpha, rho, k_) + fvm::div(alphaRhoPhi, k_) - fvm::laplacian(alpha*rho*DkEff(), k_) == alpha*rho*G - fvm::SuSp((2.0/3.0)*alpha*rho*divU, k_) - fvm::Sp(Ce(D, KK)*alpha*rho*sqrt(k_)/this->delta(), k_) + kSource() + fvModels.source(alpha, rho, k_) ); I have understood the term - fvm::SuSp((2.0/3.0)*alpha*rho*divU, k_) but still this one is unclear: alpha*rho*G |
||
|
|

|
||
|
|
|
#18 |
|
Member
Join Date: Dec 2012
Posts: 33
Rep Power: 13  |
G refers to the production of the TKE. This is written out as:
Code:
nut*(tgradU() && dev(twoSymm(tgradU()))) which is essentially a double inner over gradU(j,i) and 2*S(i,j) - 2/3 S(k,k) \delta(i,j). The first term is the velocity gradient and the second term represents the model for the Reynolds stress less the nut, which is pre-multiplied. |
|
|
|

|
|
|
|
|
#19 |
|
Senior Member
Alain Islas
Join Date: Nov 2019
Location: Mexico
Posts: 142
Rep Power: 6  |
Dear Sourav Hossain
The book is "Papanastasiou, T., Georgiou, G., & Alexandrou, A. N. (2021). Viscous fluid flow. CRC press." |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| SimpleFoam k and epsilon bounded | nedved | OpenFOAM Running, Solving & CFD | 16 | March 4, 2017 08:30 |
| [mesh manipulation] Importing Multiple Meshes | thomasnwalshiii | OpenFOAM Meshing & Mesh Conversion | 18 | December 19, 2015 18:57 |
| Creating a new field from terms of the turbulence model | HaZe | OpenFOAM Programming & Development | 15 | November 24, 2014 13:51 |
| writing execFlowFunctionObjects | immortality | OpenFOAM Post-Processing | 30 | September 15, 2013 06:16 |
| SimpleFoam k and epsilon bounded | nedved | OpenFOAM Running, Solving & CFD | 1 | November 25, 2008 20:21 |