 |
|
|
[Sponsors] | |||||
When choose sensibleInternalEnergy or sensibleEnthalpy in thermophysicalProperties |
 31Likes
31Likes
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
alexander thierfelder
Join Date: Dec 2019
Posts: 71
Rep Power: 6  |
Hi, I wonder if there is a difference in solving for the sensibleEnthalpy or sensibleInternalEnergy ? Since both are able to be calculated into one each other with p and rho, it should not matter, or does it? Are there maybe some rules when to apply which? The usage in the tutorials seem somehow random. What I already know is that we do not want to use the absoluteEnthalpy/InternalEnergy unless we are doing reactions. But even there the information I found are somehow contra intuitive:
Userguide OF7: "In most cases, we use the sensible form of energy, for which it is easier to account for energy change due to reactions." https://cfd.direct/openfoam/user-gui...hermophysical/ cfdsupport.com: "In our case without any chemistry, including heat of formation does not make any sense, so sensible variant is chosen, so the class sensibleInternalEnergy is used and the energy equation will be solved in internal energy. " https://www.cfdsupport.com/OpenFOAM-...t/node304.html |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Michael Alletto
Join Date: Jun 2018
Location: Bremen
Posts: 615
Rep Power: 16  |
Hello did you find an answer to your question?
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
|
My (possibly erroneous) reading is that:
UserGuide OF7: suggests to use either sensibleEnthalpy or sensibleInternalEnergy. Both are fine. Important is to use a sensible form of energy (among possible other choices), motivated by the possibility to add a formation energy due to chemical reactions. cfdsupport.com: given again choice between sensibleEnthalpy or sensibleInternalEnergy, the latter is chosen in scenarios in which chemistry plays no role. Does this make sense? |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Michael Alletto
Join Date: Jun 2018
Location: Bremen
Posts: 615
Rep Power: 16  |
regarding using the sensibleEnthalpy for chemical reactions i agree since usually you find the enthalpy of formation in tables. Guess the reason it is easier to measure.
I was asking mayself the question when to use the one ore the other (e or h) since analyzing the energy equation in rhoSimpleFoam I have some doubt regarding the laplacian term. In may opinion it should be possible to transform the equation of h into the one for e and visa versa. Regarding the divergence terms this is true. Regarding the laplacian term they seem to differ in a factor of cp/cv. I opened a thread: question about fvm::laplacian(turbulence->alphaEff(), he) in rhoSimpleFoam |
|
|
|

|
|
|
|
|
#5 | |
|
Senior Member
Join Date: Oct 2017
Posts: 123
Rep Power: 8  |
Quote:
|
||
|
|

|
||
|
|
|
#6 |
|
Senior Member
Join Date: Sep 2013
Posts: 353
Rep Power: 20  |
Full Energy Equation:
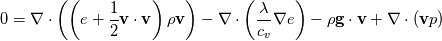 Full Energy equation formulated with Enthalpy: 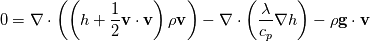 As you can see there is but one difference between these (keep in mind these equations are identical, just a different formulation). However the additional pressure work term in there is a difference from a numerical solution procedure. It is either an explicit source term when solving for e, or an implicit part of the enthalpy h. In most cases however you can split the equations above into a thermal part and the kinetic energy part. And here the thermal energy usually dominates in heat transfer, hence kinetic energy is negligible. Energy equation with removed kinetic energy: 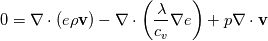 Enthalpy with removed kinetic energy: 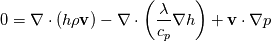 Again. Identical equations. But for example for incompressible flow, the last divergence of the velocity part is identical to zero in the first equation. So depending on the solution case, there are distinct differences. Which is why the quote from the person above me is correct. |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Join Date: Apr 2020
Location: UK
Posts: 696
Rep Power: 14  |
Bloerb - interesting - forgive my ignorance, but how does the inclusion of the pressure-work term in the internal energy (e) version stabilise the numerical solution? Does it make the equation more diagonally dominant?
|
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Michael Alletto
Join Date: Jun 2018
Location: Bremen
Posts: 615
Rep Power: 16  |
Hm lets assume we have a weakly compressible airfoil.
In the first part of the airfoil we have a favorable pressure gradient an the dot product 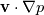 is negative. (the pressure diminishes in flow direction). This leads to a positive explicit source term and should stabilize the numerical solution. In the second part of the airfoil the dot product is positive (the pressure raised in flow direction). This leads to a positive explicit source term and should destabilize the numerical solution. So we have regions in the flow with are numerically stable and unstable. Overall this my lead on a slow convergence. If we use e as variable we solve for we have for a weakly compressible flow a source term which is nearly zero. So we don't have any source terms at all (or very small one) and this is surly preferable from a numerical point of view. |
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
Join Date: Apr 2020
Location: UK
Posts: 696
Rep Power: 14  |
Yes - that makes sense. I was mistaken though - it's not about diagonal dominance (which relies on the implicit part of the source term), but is instead about ensuring that the energy value (which must be >=0) doesn't go negative, I think. This requires that the explicit part of the source term be positive (when on the RHS of the equation). Patankar's book discusses this.
By the way, you had a small typo in your example "In the second part of the airfoil the dot product is positive (the pressure raised in flow direction). This leads to a positive explicit source term and should destabilize the numerical solution." The word marked in red should be negative. Also note that if the time derivatives are retained, then the enthalpy equation has an additional 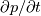 term on the right hand side, which again could destabilise matters, although pressure fluctuations should be pretty weak for weakly compressible flows. term on the right hand side, which again could destabilise matters, although pressure fluctuations should be pretty weak for weakly compressible flows.
|
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
|
@bloerb Item-6
Just to be on the save side: The signs of the diffusive terms should be flipped from neg to pos, correct? In the second formulation with the enthalpy, the term v \dot \nabla p should be -( v \dot \nabla p), correct? See e.g. Subsection 3.6.1 and Subsection 3.6.2 of 2019 book by Moukalled e.a. Thanks ahead for confirming. |
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
Join Date: Sep 2013
Posts: 353
Rep Power: 20  |
No, you can multiply them by -1 to get to the formulation you are looking for. I have a bit unconventially brought everything to the left hand side to get an =0
|
|
|
|

|
|
|
|
|
#12 |
|
Member
Hector
Join Date: Jul 2010
Location: Barcelona
Posts: 30
Rep Power: 16  |
For the sake of completeness it would be great if some of the participants of the thread could:
1) Define weakly compressible flow/fluid in this context. 2) Clarify if sensibleInternalEnergy is more stable than sensibleEnthalpy in "strongly compressible" flow/fluid. Not an issue anymore: 3) Recommend one of them for cases where there is more than one fluid (multi-phase) and one behaves as incompressible (rho = constant) and the other behaves as "strongly compressible" (rho = very variable in space and time). This is in the context of compressibleInterFoam. EDITED: The answer is to choose the most appropriate for each case because they can be chosen independently in separate datafiles for each phase (i.e. thermophysicalProperties.water ). Last edited by hectorgabriel85; February 4, 2021 at 20:18. Reason: wrong assumptions fixing |
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
Join Date: Apr 2020
Location: UK
Posts: 696
Rep Power: 14  |
Hector,
I can do the first one - a weakly compressible flow means that variations in pressure in the fluid flow do not cause a significant change in the fluid density; in other words, the Mach number is small (typically less than 0.3): and so when 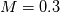 , , 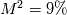 which is often assumed to be "insignificant". Alternatively, choose your tolerance and calculate your own threshold Mach number. Note that it is the "flow" that is incompressible, not the fluid. Think of air for example - can be incompressible at low speeds, e.g. wind flow around a building, or compressible at high speeds, e.g. transonic flow over an aerofoil. The beauty of incompressible flows is that you can treat density as a function of temperature only, and simplify the momentum equations considerably esp if the temperature is approximately constant or nearly constant (Boussinesq approx). which is often assumed to be "insignificant". Alternatively, choose your tolerance and calculate your own threshold Mach number. Note that it is the "flow" that is incompressible, not the fluid. Think of air for example - can be incompressible at low speeds, e.g. wind flow around a building, or compressible at high speeds, e.g. transonic flow over an aerofoil. The beauty of incompressible flows is that you can treat density as a function of temperature only, and simplify the momentum equations considerably esp if the temperature is approximately constant or nearly constant (Boussinesq approx).As for the second question (which is more stable - h or e?), I suspect it's quite problem dependent, but forum pls correct me if I am wrong. Perhaps look at the default model choices in the compressible tutorials. I vaguely recall that there was a recent patch note that explained that the default had been changed to internal energy, for the sake of stability ... again correct me forum if I am wrong. Lastly - a problem with an incompressible fluid phase in a "highly compressible" phase? Are you talking about high speed liquid droplets in a background gas? You probably need to share more details. |
|
|
|

|
|
|
|
|
#14 |
|
Member
Hector
Join Date: Jul 2010
Location: Barcelona
Posts: 30
Rep Power: 16  |
Dear Tobermory:
Comments about your 1st answer: In fluid mechanics we all say that when M < 0.3 we can treat the flow as incompressible. Thanks for bringing that up. The 9% is a good justification. But I think that is one part of the story. a. About weakly compressible: maybe when 0.2 < M < 0.4 ?? maybe 0.3 < M < 0.5 ?? b. What about low speed flow (think air flow) subjected to high pressure variations over time? Density will change significantly over time. As those are time variations maybe the flow can still be considered incompressible in space and should be treated as incompressible. |
|
|
|

|
|
|
|
|
#15 |
|
Senior Member
Join Date: Apr 2020
Location: UK
Posts: 696
Rep Power: 14  |
Agreed - the choice of limiting Mach number is subjective, and rather depends on the problem you are solving. If you are looking for highly detailed data on pressures, to compare against wind tunnel tests, then maybe a 9% accuracy is not enough. For many practical cases it is though, and it allows a simpler, often faster, incompressible solver to be used.
For b) - that's an interesting one, and once again agreed. If the timescales of the background pressure are much longer than the timescales of the flow, then the flow is in essence always in pseudo-equilibrium with the background pressure, and again it is reasonable to treat as incompressible, albeit you'd have to correct for slow drift in density by updating the kinematic viscosity. The difficulty comes when there is not an obvious "separation of scales" between the flow timescale and the timescale for the variation in background pressure .. in that case, it would be simplest to run as compressible. I suppose an example of this is an IC engine piston. |
|
|
|

|
|
 |
| Tags |
| energy, sensibleenthalpy, thermophysicalproperties |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| how can see Cp values? | immortality | OpenFOAM Post-Processing | 51 | June 18, 2021 07:19 |
| heRhoThermo - "Unknown psiThermo type" | gemxx | OpenFOAM Running, Solving & CFD | 6 | March 3, 2021 15:35 |
| WLF from OF7 | Pisolino85 | OpenFOAM | 2 | April 26, 2020 06:34 |
| compile of new combination of property in thermophisicalpropery | milad653279 | OpenFOAM Running, Solving & CFD | 4 | April 6, 2017 04:35 |
| Thermophysical properties for bouyantpimplefoam/chtmultiRegionfoam --water (any liq) | manuc | OpenFOAM Running, Solving & CFD | 10 | November 16, 2016 07:44 |