[mAlletto]

In rhoSimpleFoam and other solvers as well the energy equation has the form:

     volScalarField& he = thermo.he();    

   fvScalarMatrix EEqn     (         fvm::div(phi, he)   

    + (             he.name() == "e"         

  ? fvc::div(phi, volScalarField("Ekp", 0.5*magSqr(U) + p/rho))       

     : fvc::div(phi, volScalarField("K", 0.5*magSqr(U)))         )       - 

 fvm::laplacian(turbulence->alphaEff(), he)      ==     

    fvOptions(rho, he)     );

The if statement is to use the sensible enthalpy h or sensible internal energy e variable to be solved for.


According to the book of Wilcox "Wilcox, David C. Turbulence modeling for CFD. Vol. 3. La Canada, CA: DCW industries, 2006."


equation 5.54 the turbulent heat flux is defined as follows: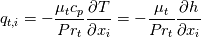


(1)


which is the equation used to calculate the turbulent heat flux for the case the sensible enthalpy h is solved for. The above equation can also written ( I hop my thermodynamic knowledge is correct):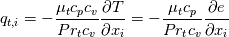


(2)


However if the sensible internal energy is solved for the turbulent heat flux is modeled like this: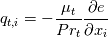


(3)




So equation (2) and (3) differ by a factor of cp/cv.



So in may opinion two slightly different equation are solved whether one uses h or e. Regarding the rest of the terms in the equation they are equivalent regardless if one solves for h or e.



Or maybe I have overseen something.



Did someone else encounter the same doubts?

[Tobermory]

Your equations are correct, but perhaps a little misleading. The turbulent Prandtl numbers in eqns 1 & 3 are different, since the definition of the turbulent diffusivity, alpha, is different depending on whether you are solving for h or e:

• For h, then and .
  
• Whereas for e we have: and .
  
• And so: .

[dlahaye]

cp/cv = gamma = 1.4 (for diatomic gas), and thus the difference matters.

Definition of Prandtl number involves c_p in case that energy equation is formulated in terms of enthalpy. No equivalent in terms of c_v seems to exist.

Not sure.

[Tobermory]

Ok, let me try explain again. Ultimately you are trying to model 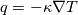, and you use the chain rule to write this as one of the following (I have left out the "at constant p" etc. limits, out of laziness):

From this you get either:

or

and you can manipulate these to get your expressions since .

The point is - the turbulent Prandtl number (an approximation) is different for the two approaches, and of course is not related to the moelcular properties of the gas. Do remember - this is a modelled diffusion term for the turbulent energy transport. And again, my point is that alphaT is different depending on whether you solve for h or e; the difference being the factor gamma.

[Bloerb]

turbulence->alphaEff() returns lambda/c_p or lambda/c_v depending on the solution variable e or h

[mAlletto]

Oh I see.


The compressible turbulence model take also the thermodynamic model as template parameter.


alphaEff is calculated as follwos in the file EddyDiffusivity.H:

        //- Return the effective turbulent thermal diffusivity for enthalpy 
        //  [kg/m/s] 
        virtual tmp<volScalarField> alphaEff() const
        {
            return this->transport_.alphaEff(alphat());
        }

the function

alphaEff(alphat())

is called int the file heThermo.C:

template<class BasicThermo, class MixtureType>
Foam::tmp<Foam::volScalarField>
Foam::heThermo<BasicThermo, MixtureType>::alphaEff
(
    const volScalarField& alphat
) const
{
    tmp<Foam::volScalarField> alphaEff(this->CpByCpv()*(this->alpha_ + alphat));
    alphaEff.ref().rename("alphaEff");
    return alphaEff;
}

and the function

 CpByCpv()

is defined in the same file as above:

template<class BasicThermo, class MixtureType>
Foam::tmp<Foam::volScalarField>
Foam::heThermo<BasicThermo, MixtureType>::CpByCpv() const
{
    const fvMesh& mesh = this->T_.mesh();

    tmp<volScalarField> tCpByCpv
    (
        new volScalarField
        (
            IOobject
            (
                "CpByCpv",
                mesh.time().timeName(),
                mesh,
                IOobject::NO_READ,
                IOobject::NO_WRITE,
                false
            ),
            mesh,
            dimless
        )
    );

    volScalarField& CpByCpv = tCpByCpv.ref();

    forAll(this->T_, celli)
    {
        CpByCpv[celli] = this->cellMixture(celli).CpByCpv
        (
            this->p_[celli],
            this->T_[celli]
        );
    }

and the function

CpByCpv(p,T)

is defined differently whether one takes the sensibleEnthalpy or internalEnergy.


For the sensibleEntalpy we find the function in sensibleEnthalpy.H (it returns 1)

            //- Cp/Cp []
            scalar CpByCpv
            (
                const Thermo& thermo,
                const scalar p,
                const scalar T
            ) const
            {
                return 1;
            }

and for sensibleInternalEnergy in sensibleInternalEnergy.H (it returns gamma)

            //- Ratio of specific heats Cp/Cv []
            scalar CpByCpv
            (
                const Thermo& thermo,
                const scalar p,
                const scalar T
            ) const
            {
                #ifdef __clang__
                // Using volatile to prevent compiler optimisations leading to
                // a sigfpe
                volatile const scalar gamma = thermo.gamma(p, T);
                return gamma;
                #else
                return thermo.gamma(p, T);
                #endif
            }

[mAlletto]

Ok so we can say the the same equations are solve regardless one take h or e as quantity you solve for.



The difference in both equation may lay in the numerical stability since different explicit source terms appear in the equations.


For this see also When choose sensibleInternalEnergy or sensibleEnthalpy in thermophysicalProperties

[melabbassi]

Originally Posted by Bloerb

turbulence->alphaEff() returns lambda/c_p or lambda/c_v depending on the solution variable e or h

This is where it gets confusing because it should be alpha = lambda/(rho * cp).

and the diffusion term in the energy equation should be:

fvm::laplacian(rho * turbulence->alphaEff(), he)

if of course, the unit of alphaEff is [m²/s] (according to SI)... but it's not! Strangely enough, in OpenFOAM, the unit for alphaEff is [kg/(m s)].

source:
https://cfd.direct/openfoam/free-sof...or-the-future/