 |
|
|
[Sponsors] | |||||
Time-step size for coupled implicit simulations |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
Pietro
Join Date: Jun 2021
Location: London
Posts: 40
Rep Power: 5  |
Hello,
I have a question about what is the best choice for time-step size in fully implicit simulations (coupled implicit solver in STAR-CCM+). From what I understand, in fully implicit simulations, at each time-level a steady simulation is performed via the pseudo-transient strategy. As a consequence, 3 different values need to be set: 1) Courant (or CFL) number: this number defines the pseudo time-step of the steady simulations which are performed at each time-level and is NOT related to the time-step size of the unsteady simulation. The higher Courant, the higher will be the convergence rate (for a given number of iterations) of the steady simulation. However, for too high Courant, the algorithm may diverge 2) Time-step size: this number represents the intervals in physical time according to which the steady simulations are performed. Fully implicit methods are 1st order in accuracy, therefore the lower the time-step size, the higher will be the accuracy in a linear fashion. A solution with high time-step size will be always stable and always physical, however not time-accurate 3) Number of inner iterations: the steady simulations inside each time-step are solved with iterative procedures, therefore at each time-level a certain number of iterations is required to obtain convergence Considering this, I usually set my Courant number as high as possible (e.g. 50), as long as it leads to convergence of the steady simulation. The choice of time-step size and number of inner iterations however is not trivial. For very low time-step sizes, the accuracy increases, but it is not possible to employ a high number of inner iterations as the cost of the simulation would then be too high. Therefore, the steady simulation at each time-level does not converge. On the other hand, for higher time-step sizes, it is possible to use 50 or 100 iterations, which will lead the steady simulations to converge, but the time-accuracy will not be as high. Is there any rule of thumb for choosing the time-step size and number of inner iterations? In a previous post I read that you should never exceed 15 inner iterations. Is this true? Or is it strongly dependent on the physics of the simulation? Pietro |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
Knowing that you can always lower your time-step size to make the solution more stable and more accurate, you almost never want to use a high number of inner iterations.
A Courant number of 50 is equivalent to an under-relaxation factor of ~0.98. So after 2 inner iterations you are more than 0.9996 of your time-step size and after 3 inner iterations you are more than 0.999992 of your time-step size. If the solver was not stable enough, it would've blown up already around here. If you set the number of inner iterations to 15, you are spending another 12 inner iterations to advance the simulation by a tiny fraction of the time-step size at hopes of achieving.... what? It's better to spend those 12 inner iterations doing another 4 time-steps. You could have even done 4 smaller time-steps and gotten a more accurate solution in the same time. Now this situation holds when the solution can converge fast with a high Courant number. So when do we absolutely need a high number of iterations possibly with a lower Courant number? You need this to make sure non-linearities between equations are properly coupled together, i.e. when non-linear coupling is stalling your convergence. |
|
|
|

|
|
|
|
|
#3 |
|
Member
Pietro
Join Date: Jun 2021
Location: London
Posts: 40
Rep Power: 5  |
Hi Lucky Tran,
Thanks for the answer. While I agree that for lower time-step size you gain accuracy, I cannot understand how you link the pseudo time-step size (i.e. CFL number of steady simulation, or under-relaxation factor, which at the end represent all the same thing) to the physical time inside a time-step of the implicit simulation, writing that 'after 2 iterations you are already at 0.9996 of the time-step size'. From how I understand it (and I am probably missing something!) the pseudo-transient simulations occurring at each time-level are solved with algorithms such as SIMPLE. These are iterative algorithms that require under-relaxation to be stable. The lower CFL, the more 'under-relaxed' and therefore stable will be the pseudo-transient simulation. The SIMPLE algorithm needs a (usually) relatively high number of iterations to converge, depending on the physics of the problem and on the initial conditions. For example, when you run with the steady solver on STAR-CCM+, you usually run for 200-1000 iterations at least before reaching convergence. I cannot immagine a steady simulation converging in only 2 or 3 iterations (unless the initial conditions are basically the same of the converged solution). I attach as an example the pseudo-transient result inside a time-step of my implicit simulation, showing how the shear moment converges only after 200 inner iterations and how for 50 iterations is not converged. Long story short: I agree that low time-step size = higher accuracy, but it seems to me that you should always make sure that your pseudo-transient simulation has converged inside such time-level and 2-3 iterations sound very low for that. Pietro |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
I recommend to read up on implicit underrelaxation. There is an algebraic relation between Courant number, an implicit under-relaxation factor, and the physical timestep. For implicit solvers, even steady equations have a time-step under-the-hood which is related to the Courant number.
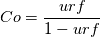 SIMPLE is just one specific algorithm for solving the pressure-velocity coupling problem, i.e. the continuity and momentum equations. SIMPLE does not do non-orthogonal corrections, relying on outer iterations to do this. Because of this, it's naturally very unstable and requires a lot of under-relaxation. There are other algorithms that are much less unstable (various SIMLPE variants, and non-SIMPLE approaches). You can do transient simulations with 1 inner iteration per time-step. That's exactly what PISO is designed to do for example. You can do this with a pseudo-transient solver if you crank up your Courant number to very large values towards infinity (some texts recommend 1e6, I personally use 2e6). Of course your time-step size needs to be small enough or it blows up. You say you can't imagine it... But people do this all the time. Steady simulations don't reach their steady solution in 1 iteration because the solution is not simply not steady. If you guess the solution as the initial guess, it does converge in 1 iteration. Your plots show the classical problem of stable but not accurate. You converge within each time-step by doing a billion iterations, and it is meaningless because the solution is inaccurate anyway. That's why we recommend not to do too many. If there is ever a situation where you need that many inner iterations per time-step, then you are probably already doing something wrong. That is, you should repeat that plot with the same CFL number and inner iterations, but lower the physical time-step size. |
|
|
|

|
|
 |
| Tags |
| courant number, implicit, pseudo time dual time, time accuracy |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| pimpleDyMFoam computation randomly stops | babapeti | OpenFOAM Running, Solving & CFD | 5 | January 24, 2018 05:28 |
| Stuck in a Rut- interDyMFoam! | xoitx | OpenFOAM Running, Solving & CFD | 14 | March 25, 2016 07:09 |
| Superlinear speedup in OpenFOAM 13 | msrinath80 | OpenFOAM Running, Solving & CFD | 18 | March 3, 2015 05:36 |
| Micro Scale Pore, icoFoam | gooya_kabir | OpenFOAM Running, Solving & CFD | 2 | November 2, 2013 13:58 |
| Could anybody help me see this error and give help | liugx212 | OpenFOAM Running, Solving & CFD | 3 | January 4, 2006 18:07 |