Isentropic flow relations
From CFD-Wiki
(→Critical values) |
(→Isentropic flow) |
||
| Line 3: | Line 3: | ||
Constant entropy flow is called Isentropic flow. | Constant entropy flow is called Isentropic flow. | ||
| - | From a consideration of the second law of thermodynamics, a reversible flow maintains a constant value of entropy | + | From a consideration of the second law of thermodynamics, a reversible flow maintains a constant value of entropy. |
| - | + | In the theory of streamtubes, isentropic flow is the basis for compressible flow. | |
| + | |||
| + | The well known incompressible flow does not apply if <math>M << 1</math> is violated. | ||
Therin | Therin | ||
| Line 21: | Line 23: | ||
In the following all thermodynamic properties are related to their '''properties ''at rest''''' (u=0). | In the following all thermodynamic properties are related to their '''properties ''at rest''''' (u=0). | ||
| - | From the energy equation for a frictionless flow | + | From the energy equation for a frictionless, adiabatic flow |
<math> \frac{u^2}{2}+h=h_t </math> | <math> \frac{u^2}{2}+h=h_t </math> | ||
Revision as of 20:35, 30 January 2008
Contents |
Isentropic flow
Constant entropy flow is called Isentropic flow.
From a consideration of the second law of thermodynamics, a reversible flow maintains a constant value of entropy.
In the theory of streamtubes, isentropic flow is the basis for compressible flow.
The well known incompressible flow does not apply if 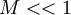 is violated.
Therin
is violated.
Therin
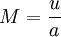
is called the Mach-number. It is the relation between the flow-velocity u (fluid or object) and the speed of sound a in the surrounding medium.
In a caloric ideal gas the speed of sound depends on the absolute temperature T (K), the adiabatic exponent 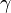 and the specific gas constant R (J/(kg K))
and the specific gas constant R (J/(kg K))
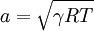 .
.
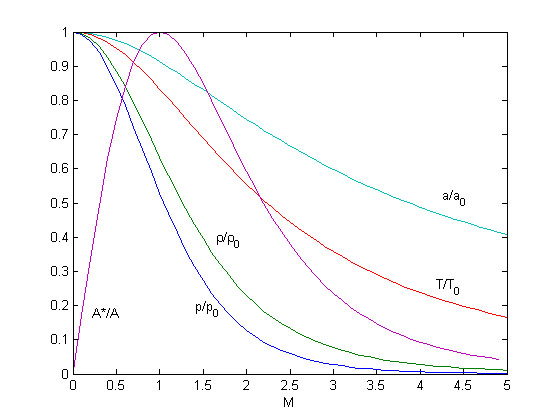
In this case all thermodynamic properties (temperature, pressure, density and speed of sound) can be expressed with explicit formulas which are functions of the Mach-number!
In the following all thermodynamic properties are related to their properties at rest (u=0).
From the energy equation for a frictionless, adiabatic flow
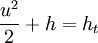
you will get that the enthalpy at rest ht is allways the same regardless of an isentropic or non-isentropic state change.
As a matter of fact - 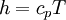 - the temperature is it as well.
In contrary the pressure depends on how the gas is brougt to rest. The pressure at rest is only obtained if the state change is isentropic. If the entropy changes the pressure at rest changes as well, e.g. when passing a shock.
- the temperature is it as well.
In contrary the pressure depends on how the gas is brougt to rest. The pressure at rest is only obtained if the state change is isentropic. If the entropy changes the pressure at rest changes as well, e.g. when passing a shock.
Pressure
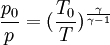
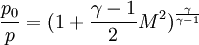
Temperature and speed of sound
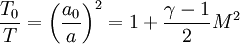
Density
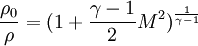
Critical values
Values which can be found at M=1 (speed of sound) are sometimes called critical values. They are marked with the superscript *.
They differ from the properties at rest only by a constant value and are therefore used as reference values as well.
In the special case for gases which contain two atoms (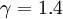 ) one gets:
) one gets:
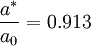
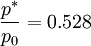
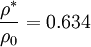
Critical cross-section
The cross-section 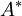 in a nozzle where M equals 1 is often used as a reverence, even if M=1 is never reached.
in a nozzle where M equals 1 is often used as a reverence, even if M=1 is never reached.
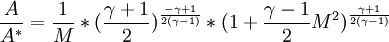
![\left( \frac{A}{A^*} \right)^2 = \frac{1}{M^2} \left[ \frac{2}{\gamma+1} \left( 1 + \frac{\gamma-1}{2}M^2\right)\right]^{(\gamma+1)/(\gamma-1)}](/W/images/math/9/8/3/9836ff77bd3c40808b9533d36e2d9543.png)
Summary
As one can see all thermodynamic properties decrease with increasing Mach-number.
Literature
Spurk, J.H. (2004), Strömungslehre. Eine Einführung in die Theorie der Strömungen, ISBN 3-540-40166-0, 5.th Ed., Springer-Verlag, Berlin..