A roughness-dependent model
From CFD-Wiki
Contents |
Two-equation 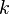 -
- eddy viscosity model
eddy viscosity model
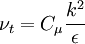 | (1) |
where:
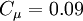
One-equation eddy viscosity model
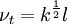 | (2) |
Algebraic eddy viscosity model
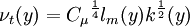 | (3) |
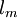 is the mixing length.
is the mixing length.
Algebraic model for the turbulent kinetic energy
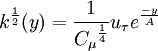 | (4) |
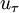 is the shear velocity and
is the shear velocity and 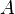 a model parameter.
a model parameter.
For steady open channel flows in local equilibrium, where the energy production is balanced by the dissipation, from the modeled 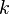 -equation [Nezu and Nakagawa (1993)] obtained a similar semi-theoretical equation.
-equation [Nezu and Nakagawa (1993)] obtained a similar semi-theoretical equation.
Algebraic model for the mixing length
For local equilibrium, an extension of von Kármán’s similarity hypothesis allows to write, with equation (4) [Absi (2006)]:
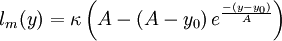 | (5) |
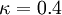 ,
, 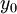 is the hydrodynamic roughness.
For a smooth wall (
is the hydrodynamic roughness.
For a smooth wall (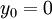 ):
):
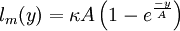 | (6) |
the algebraic eddy viscosity model is therefore
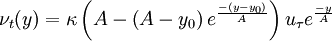 | (7) |
The mean velocity profile
For local equilibrium, we are able to find the mean velocity profile 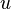 from the turbulent kinetic energy
from the turbulent kinetic energy 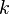 (equation 4) and the mixing length
(equation 4) and the mixing length 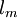 (equation 5), by:
(equation 5), by:
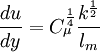 | (8) |
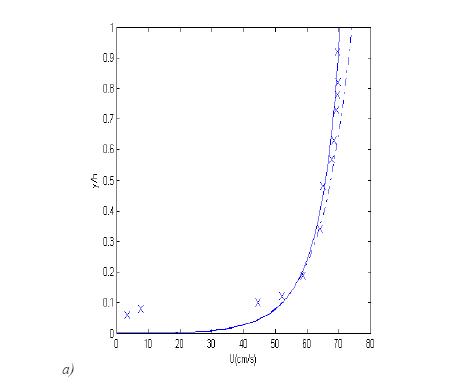
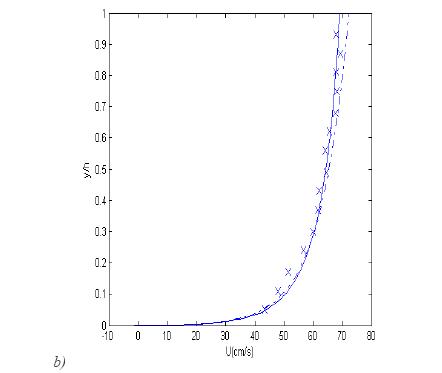
Figure (1) shows that the velocity profile obtained from equations (8), (4) and (5) (solid line) is more accurate than the logarithmic velocity profile (dash-dotted line).
Figure 1, Vertical distribution of mean flow velocity.
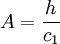 ;
;  ;
Dash-dotted line: logarithmic profile; solid line: obtained from equation (8); symbols: experimental data ([Sukhodolov et al. (1998)]). a) profile 2:
;
Dash-dotted line: logarithmic profile; solid line: obtained from equation (8); symbols: experimental data ([Sukhodolov et al. (1998)]). a) profile 2: 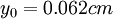 ;
; 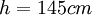 ;
; 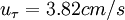 . b) profile 4:
. b) profile 4: 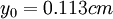 ;
; 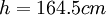 ;
; 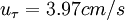 ; (values of
; (values of 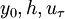 are from [Sukhodolov et al. (1998)]); Figure from [Absi (2006)].
are from [Sukhodolov et al. (1998)]); Figure from [Absi (2006)].
References
- Absi, R. (2006), "A roughness and time dependent mixing length equation", Journal of Hydraulic, Coastal and Environmental Engineering, (Doboku Gakkai Ronbunshuu B), Japan Society of Civil Engineers, Vol. 62, No. 4, pp.437-446.
- Nezu, I. and Nakagawa, H. (1993), "Turbulence in open-channel flows", A.A. Balkema, Ed. Rotterdam, The Netherlands.
- Sukhodolov, A., Thiele, M. and Bungartz, H. (1998), "Turbulence structure in a river reach with sand bed", Water Resour. Res., Vol. 34, pp. 1317-1334.