Reynolds stress model (RSM)
From CFD-Wiki
Contents |
Introduction
The Reynolds Stress Models (RSM), also known as the Reynolds Stress Transport Models, are higher level turbulence closures and represent the most complete classical turbulence model. The method of closure employed is usually called a Second Order Closure. This modelling approach originates from the works by Chou (1945) and Rotta (1951). In Reynolds Stress Models, the eddy viscosity approach is avoided and the individual components of the Reynolds stress tensor are directly computed. These models rely on the exact Reynolds stress transport equation. They are able to account for complex interactions in turbulent flow fields, such as the directional effects of the Reynolds stresses.
Shortcomings of Eddy-viscosity based models
Eddy-viscosity based models like the 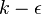 and the
and the 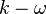 models have significant shortcomings in complex, real-life turbulent flows that are often encountered in engineering applications. In flows with high degrees of anisotropy, significant streamline curvature, flow separation, flows with zones of re-circulation or flows influenced by mean rotational effects, the performance of such models is unsatisfactory (Craft (1996)).
models have significant shortcomings in complex, real-life turbulent flows that are often encountered in engineering applications. In flows with high degrees of anisotropy, significant streamline curvature, flow separation, flows with zones of re-circulation or flows influenced by mean rotational effects, the performance of such models is unsatisfactory (Craft (1996)).
Eddy viscosity based closures cannot account for the limiting states of turbulence. In decaying turbulent flows, it has been observed that the state of turbulence rapidly approaches an isotropic state with equipartition of the turbulent kinetic energy among the components of the Reynolds stresses. Eddy-viscosity based models can never replicate this return to isotropy behaviour. Eddy-viscosity based models cannot replicate the behaviour of turbulent flows in the Rapid Distortion limit, where the turbulent flow essentially behaves as an elastic medium (instead of viscous).
Reynolds Stress Models have an clear advantage over lower-order models for such flows where the transport of terms like the Reynolds stress or heat flux, play important roles. This is because the physics of the transport of second-moment terms can be built into the second-order models.
Equations
The Reynolds stress model involves calculation of the individual Reynolds stresses, 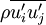 , using differential transport equations. The individual Reynolds stresses are then used to obtain closure of the Reynolds-averaged momentum equation.
, using differential transport equations. The individual Reynolds stresses are then used to obtain closure of the Reynolds-averaged momentum equation.
The exact transport equations for the transport of the Reynolds stresses, 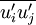 , may be written as follows:
, may be written as follows:
![\frac{\partial}{\partial t}\left(\rho \overline{u'_iu'_j}\right) + \frac{\partial}{\partial x_{k}}\left(\rho u_{k} \overline{u'_iu'_j}\right) = - \frac{\partial}{\partial x_k}\left[\rho \overline{u'_iu'_ju'_k} + \overline{p'\left(\delta_{kj}u'_i + \delta_{ik}u'_j\right)}\right]](/W/images/math/9/b/5/9b5c9395809ce17bf11ec78d03ab516a.png)
![+ \frac{\partial}{\partial x_k}\left[{\mu \frac{\partial}{\partial x_k}\left(\overline{u'_iu'_j}\right)}\right] - \rho\left(\overline{u'_iu'_k}\frac{\partial u_j}{\partial x_k}+\overline{u'_ju'_k}\frac{\partial u_i}{\partial x_k}\right)](/W/images/math/9/1/2/91259a778699a4c7759fc0e0207065aa.png)
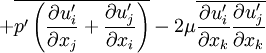
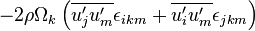
or
Local Time Derivate + 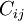 =
= 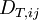 +
+ 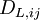 +
+ 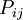 +
+ 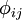 -
- 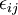 +
+ 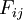
where 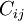 is the Convection-Term,
is the Convection-Term, 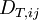 equals the Turbulent Diffusion,
equals the Turbulent Diffusion, 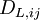 stands for the Molecular Diffusion,
stands for the Molecular Diffusion, 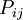 is the term for Stress Production,
is the term for Stress Production, 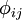 is for the Pressure Strain,
is for the Pressure Strain, 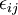 stands for the Dissipation and
stands for the Dissipation and 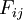 is the Production by System Rotation.
is the Production by System Rotation.
Of these terms, 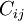 ,
, 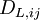 ,
, 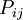 , and
, and 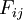 do not require modelling. However,
do not require modelling. However, 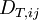 ,
, 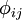 , and
, and 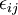 have to be modelled for closing the equations. The fidelity of the Reynolds stress model depends on the accuracy of the models for the turbulent transport, the pressure-strain correlation and the dissipation terms.
have to be modelled for closing the equations. The fidelity of the Reynolds stress model depends on the accuracy of the models for the turbulent transport, the pressure-strain correlation and the dissipation terms.
Modeling the Pressure-Strain Term
Return-to-isotropy models
For an anisotropic turbulence, the Reynolds stress tensor,
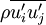 , is usually anisotropic. The
second and third invariances of the Reynolds-stress anisotropic
tensor
, is usually anisotropic. The
second and third invariances of the Reynolds-stress anisotropic
tensor 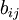 are nontrivial, where
are nontrivial, where
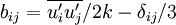 and
and
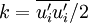 . It is naturally to suppose
that the anisotropy of the Reynolds-stress tensor results from the
anisotropy of turbulent production, dissipation, transport,
pressure-stain-rate, and the viscous diffusive tensors. The
Reynolds-stress tensor returns to isotropy when the anisotropy of
these turbulent components return to isotropy. Such a correlation is
described by the Reynolds stress transport equation. Based on these
consideration, a number of turbulent models, such as Rotta's model
and Lumley's return-to-isotropy model, have been established.
. It is naturally to suppose
that the anisotropy of the Reynolds-stress tensor results from the
anisotropy of turbulent production, dissipation, transport,
pressure-stain-rate, and the viscous diffusive tensors. The
Reynolds-stress tensor returns to isotropy when the anisotropy of
these turbulent components return to isotropy. Such a correlation is
described by the Reynolds stress transport equation. Based on these
consideration, a number of turbulent models, such as Rotta's model
and Lumley's return-to-isotropy model, have been established.
Rotta's model describes the linear return-to-isotropy behavior of a low Reynolds number homogenous turbulence in which the turbulent production, transport, and rapid pressure-strain-rate are negligible. The turbulence dissipation and slow pressure-strain-rate
are preponderant. Under these cirsumstance, Rotta suggested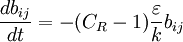
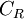 is called the Rotta constant.
is called the Rotta constant.
Modeling Turbulent Diffusive Transport
Modeling the Dissipation Rate
Model constants
The constants suggested for use in this model are as follows:
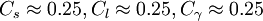
Model variants
LRR, Launder-Reece-Rodi
Launder, B. E., Reece, G. J. and Rodi, W. (1975), "Progress in the Development of a Reynolds-Stress Turbulent Closure.", Journal of Fluid Mechanics, Vol. 68(3), pp. 537-566.
SSG, Speziale-Sarkar-Gatski
Speziale, C.G., Sarkar, S., Gatski, T.B. (1991), "Modeling the Pressure-Strain Correlation of Turbulence: an Invariant Dynamical Systems Approach", Journal of Fluid Mechanics, Vol. 227, pp. 245-272.
Johansson & Hallbäck
Johansson, A. V. and Hallbäck, M. (1994), "Modelling of rapid pressure—strain in Reynolds-stress closures", Journal of Fluid Mechanics, Vol. 269, pp. 143-168.
Mishra & Girimaji
Mishra, A. A. and Girimaji, S. S. (2017), "Toward approximating non-local dynamics in single-point pressure–strain correlation closures", Journal of Fluid Mechanics, Vol. 811, pp. 168-188.
Performance, applicability and limitations
Implementation issues
References
Kemal Hanjalić and Brian Launder (2011), Modelling Turbulence in Engineering and the Environment: Second-Moment Routes to Closure, ISBN 978-0521883986, Cambridge University Press.
Chou, P. (1945), "On velocity correlations and the solutions of the equations of turbulent fluctuation.", Quarterly of Applied Mathematics, Vol. 3(1), pp. 38-54.
Rotta, J. (1951), "Statistische theorie nichthomogener turbulenz.", Zeitschrift für Physik A, Vol. 129(6), pp. 547-572.
Launder, B. E., Reece, G. J. and Rodi, W. (1975), "Progress in the Development of a Reynolds-Stress Turbulent Closure.", Journal of Fluid Mechanics, Vol. 68(3), pp. 537-566.
Craft, T., Launder, B. and K. Suga (1996), "Development and application of a cubic eddy-viscosity model of turbulence.", International Journal of Heat and Fluid Flow, Vol. 17, pp. 108-115.
