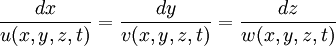Streamline
From CFD-Wiki
A line in the fluid whose tangent is everywhere parallel to the local velocity vector 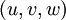 instantaneously is a streamline. The family of streamlines at time
instantaneously is a streamline. The family of streamlines at time 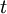 are solutions of
are solutions of
Streamlines cannot intersect since the velocity at any point is unique.
In two dimensions and for axisymmetric flows, a stream function exists which is constant on each streamline.