 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Super Moderator
|
http://www.kxcad.net/ansys/ANSYS_CFX.../i1311648.html
It is stated in the CFX theory (above link) that when one selects the high resolution scheme as below 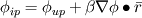 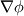 is the value at the upwind node. is the value at the upwind node.On the other hand when user selects the specified blend factor for 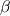 (between 0 and 1), (between 0 and 1), 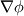 is equal to the average of the adjacent nodal gradients. I wanna know, this scheme is the upwind or central differencing scheme? is equal to the average of the adjacent nodal gradients. I wanna know, this scheme is the upwind or central differencing scheme?http://my.fit.edu/itresources/manual...ug/node992.htm Where as in fluent user guide (above link) 2nd order upwind scheme is given by following formula 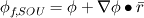 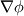 is the gradient of is the gradient of 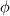 in the upwind cell in the upwind cellBoth high resolution (CFX) and 2nd order upwind scheme (Fluent) are based on the principles by Barth and Jespersen [1] so that no new extrema is introduced in the solution, therfore monotonic behavior is preserved. 1. Does it mean that the high resolution scheme of CFX and 2nd order upwind scheme of fluent are equivalent. 2. Does it mean that the CFX 2nd order scheme is more like a baised 2nd order scheme with one term of upwind and 2nd term (anti diffusive term) is central differencing type? 3. Will 2nd order upwind (CFX definition) will make the solution worst than even 1st order upwind scheme? References: [1] Barth and Jespersen "The design and application of upwind schemes on unstructured meshes" . Technical Report AIAA-89-0366, AIAA 27th Aerospace Sciences Meeting, Reno, Nevada, 1989. |
|
|
|

|
|
|
|
|
#3 | |||
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,703
Rep Power: 143     |
It has been a while since I looked into this stuff, but this is my understanding:
Quote:
Quote:
Quote:
|
||||
|
|

|
||||
|
|
|
#5 | |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,703
Rep Power: 143     |
Quote:
So I cannot see anything which suggests beta=0.5 gives you CDS. |
||
|
|

|
||
|
|
|
#7 |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,703
Rep Power: 143     |
No, read the full sentence - the del (phi) is redefined in CDS, so the high res scheme cannot become the CDS as the del (phi) terms are different.
|
|
|
|

|
|
|
|
|
#8 | |
|
New Member
A.R. Baserinia
Join Date: Jan 2010
Location: Canada
Posts: 24
Rep Power: 16  |
Quote:
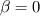 leads to 1st-order upwind, and leads to 1st-order upwind, and 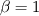 leads to 2nd-order upwind. leads to 2nd-order upwind. 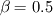 is a blend of 1st- and 2nd-order upwind schemes which supposedly is more accurate than 1st-order scheme, but also more stable than 2nd-order scheme. You should use is a blend of 1st- and 2nd-order upwind schemes which supposedly is more accurate than 1st-order scheme, but also more stable than 2nd-order scheme. You should use 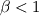 if and only if the 2nd-order upwind fails to converge. if and only if the 2nd-order upwind fails to converge.
|
||
|
|

|
||
|
|
|
#10 |
|
Super Moderator
Glenn Horrocks
Join Date: Mar 2009
Location: Sydney, Australia
Posts: 17,703
Rep Power: 143     |
This thread is getting tiresome. Please read the documentation.
It clearly says that the CDS has a different implementation to the upwinding schemes so you won't be able to get the CDS from any version of upwinding schemes - first order, hybrid or high res. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Second Order Upwind: Residuals | enricokr | FLUENT | 28 | January 2, 2018 17:41 |
| Changing LimitedLinear to blend with 2nd order upwind instead of 1st order upwind | stevenvanharen | OpenFOAM Programming & Development | 0 | April 11, 2011 05:54 |
| First Order Upwind X High-Order Upwind (CUBISTA) Schemes | buscapeh | Main CFD Forum | 0 | September 23, 2010 22:32 |
| second order upwind cause divege !! | khsiavash | Main CFD Forum | 0 | August 4, 2009 15:00 |
| First order upwind | leung | FLUENT | 2 | June 13, 2004 08:09 |