[94bb494nd41f]

hey guys,

I am currently writing my Bachelor thesis using fluent. I am using the third order MUSCL Scheme which obtains, just like QUICK and stated in the name of the Scheme, a third order accuracy.

So I took a look into the Handbook to see how this thing is working. But instead of understanding it, I just got realy confused.

The third order MUSCL Scheme works by blending a central differencing and a second-order upwind scheme. Both of those schemes are second order accurate, so how does the whole things goes third order?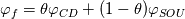


(CD: Central differential; SOU: second order upwind)

Hope anyone can Help me. I am new to this forum and hope i didnt make any large mistakes.

I am using Ansys Fluent 18.1 and got my information form the Handbook (theory guide - Solver theory - Spatial discretization)

Regards

an mechanical engineer

[LuckyTran]

MUSCL uses three-points, compared to 2 for 2nd order upwind and 1 for 1st order upwind. It should not take too much imagination to guess that MUSCL might be 3rd order accurate.

Originally Posted by 94bb494nd41f

Both of those schemes are second order accurate, so how does the whole things goes third order?

For any particular scheme, you must do the math (easier said than done) to determine the order of accuracy. Otherwise all schemes can be written as a combination of blended 1st order upwind schemes, which would imply that there are no higher order schemes beyond 1st order.

I remember looking into this topic at one point. I vaguely recall that MUSCL (or maybe it was QUICK) is 3rd order accurate for interpolating to face values, but that the end result for the cell values is still 2nd order.

[94bb494nd41f]

What you are saying makes a lot of sense but i dont get this last one; do you mean the interpolation with MUSCl is third order but the computed cell values are still second order? this sound more like using a wrong, second order integration method.

Originally Posted by LuckyTran

I remember looking into this topic at one point. I vaguely recall that MUSCL (or maybe it was QUICK) is 3rd order accurate for interpolating to face values, but that the end result for the cell values is still 2nd order.

[LuckyTran]

Originally Posted by 94bb494nd41f

do you mean the interpolation with MUSCl is third order

You need to finish the sentence. 3rd order for what? MUSCL interpolates for face values, which is neither the face flux which you need nor the the cell value that you are integrating for. Sometimes the distinction between face value and face flux can be very important.

Furthermore, it only means the advective face values are 3rd order accurate. The diffusive fluxes are still, usually central differencing, 2nd order.

All I'm saying is, don't be so surprised if you find out MUSCL isn't actually 3rd order. It does not help that I cannot recall the particular paper where these supposed results were established.

[fce]

I just came across this. I know it is an old post but in case anyone else looks for further explanations there is a nice paper on this:

https://arc.aiaa.org/doi/10.2514/1.J060773