 |
|
|
[Sponsors] | |||||
|
|
|
#21 |
|
Senior Member
Join Date: May 2012
Posts: 546
Rep Power: 15  |
In my mind (most likely naive) I think of stability only in terms of the coefficient matrix we create. If the matrix satisfies the Scarborough criterion then it will be numerically stable for iterative methods. So basically, ensuring diagonal dominance of the matrix is enough.
|
|
|
|

|
|
|
|
|
#22 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,773
Rep Power: 71    |
Quote:
Unfortunately, the matrix analysis for the numerical stability has some differences from the convergence criterion of iterative methods. In iterative method you need the error going to zero as n->Inf. For the stability analysis you need only that the error is not amplified. There are cases where the matrix analysis does not provide a clear answer to the stability and only the von Neumann's analysis proveds the answer. Then, you can have some criterion that says the scheme is stable asymptotically but the error grows before to reach this stability condition. In general, you need to evaluate the spectral radius of the matrix, the diagonal dominance being not useful. |
||
|
|

|
||
|
|
|
#23 | |
|
Senior Member
Join Date: May 2012
Posts: 546
Rep Power: 15  |
Quote:
This is interesting. Analyzing the matrix gives the correct (sufficient) stability criterion for many (perhaps trivial?) equations. Do you mean that the condition is too restrictive? Could you provide the example where von Neumann analysis is the only way to obtain the correct answer? |
||
|
|

|
||
|
|
|
#24 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,773
Rep Power: 71    |
Quote:
One of the example I use during my CFD course is the FTCS scheme for the linear wave equation. Using the matrix analysis and the Gershgorin criterion to localize the spectral radius you cannot obtain a final conclusion. Conversely, the von Neumann's analysis shows that the scheme is unconditionally unstable. |
||
|
|

|
||
|
|
|
#25 | |
|
Senior Member
Join Date: May 2012
Posts: 546
Rep Power: 15  |
Quote:
To make sure I do not misinterpret what you mean by FTCS for the wave equation, could you also please provide your discretization? |
||
|
|

|
||
|
|
|
#26 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,773
Rep Power: 71    |
||
|
|

|
|
|
|
|
#27 |
|
Senior Member
Join Date: May 2012
Posts: 546
Rep Power: 15  |
Just wondering how you create the first order derivative in time. Do you use a one-sided difference for this? Sorry I am not very familiar with the wave equation so this is not obvious for me. Anyhow, I attach a common (I guess) way to discretize it but this would be O(dt^2, dx^2) not O(dt, dx^2). 
|
|
|
|

|
|
|
|
|
#28 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,773
Rep Power: 71    |
No, I am talking about the first order linear wave equation
du/dt + c du/dx =0 |
|
|
|

|
|
|
|
|
#29 |
|
Senior Member
Join Date: May 2012
Posts: 546
Rep Power: 15  |
Ok, that explains it.
This equation can easily be shown to be unstable simply by looking at the matrix I think. With all first order explicit formulations it is easy to find the stability criterion by comparison to how a similar steady-state solution using the Jacobi method would look like. This is because the Jacobi method mimics the first order explicit method when we use the maximum allowable time-step (as a side-note this is also why the Jacobi method is such a slow method to use for iterative solutions). A steady state discretization of the advection equation (or similar) yields a matrix with zeros along the main diagonal and as such it violates the Scarborough criterion. Well, it is possible to manipulate the matrix using a left- or right-shift with proper modification of the boundary conditions and get a solution, but this is outside of this discussion I think. |
|
|
|

|
|
|
|
|
#30 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,773
Rep Power: 71    |
Quote:
no, you must study the matrix for the transient, that is u(i,n+1)=u(i,n)-c*dt*0.5*(u(i+1,n)-u(i-1,n))/h The matrix has 1 in the main diagonal and 0.5*cfl and -0.5*cfl in the adjacent diagonals. The Gershogorin criterion cannot answer to the stabilty constraint. |
||
|
|

|
||
|
|
|
#31 | |
|
Super Moderator
|
Quote:
Be careful when using eigenvalues when the matrix is non-normal, which is usually the case for hyperbolic problems. Eigenvalues being less than 1 in magnitude ensures that you are asymptotically stable. If all eigenvalues are less than one in magnitude, then as 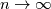 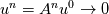 so there is no blowup. But if the matrix is non-normal, then 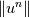 can increase initially before it eventually decreases. This may become a problem if the growth is enough that non-linearity becomes important. Then linear stability in the sense of eigenvalues may not be enough. can increase initially before it eventually decreases. This may become a problem if the growth is enough that non-linearity becomes important. Then linear stability in the sense of eigenvalues may not be enough.
|
||
|
|

|
||
|
|
|
#32 |
|
Super Moderator
|
Stability issues are discussed in a bad and wrong way in many CFD books. This is the problem even in the recent book
Hirsch, Numerical computation of internal and external flows. Volume 1 There are too many mistakes in Chapter 7. For example in Section 7.2.1, it is said that 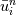 = exact solution of scheme, obtained on computer with infinite precision = exact solution of scheme, obtained on computer with infinite precision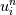 = computed solution due to finite precision = computed solution due to finite precisionThen 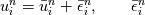 = error due to finite precision. = error due to finite precision.The book then goes on to assume that  so that 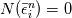 and claims error satisfies same equation. This is simply wrong. Both of the equations  cannot be true. In reality, what the computer implements is 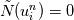 where 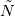 is different from is different from 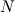 due to finite precision. due to finite precision.However, we can do the analysis more carefully and show that if the scheme is linearly stable, then round-off errors will not grow unboundedly. I would recommend reading math oriented books for a clear explanation of stability. I have not seen above kind of mistakes being made in books written by mathematicians or those with better math training. (I am an engineer myself by training and I am not trying to criticise engineers by saying this.) A really good book is Gustafsson, Kreiss, Oliger: Time dependent problems and difference methods. |
|
|
|

|
|
|
|
|
#33 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,773
Rep Power: 71    |
Quote:
Yes, the issue in some textbooks is in the introduction of a homogeneous equation for the error. But the error equation is not homogeneous at all. That is a part I tried to highlight in my note. I addressed also the statements of Hirsch, as well as Anderson and other authors. However, von Neumann's paper did not introduce at all an equation for the error. His analysis is done on the discrete equation for solving the variable and shows clearly that the numerical stability is an issue also for infinite precision. |
|
|
|

|
|
|
|
|
#34 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,773
Rep Power: 71    |
Quote:
Yes, but this analysis is strictly related to the spectral analysis in the von Neumann's theory. Often Gershgorin provides the rapid answer. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Von Neumann Stability | mathgra | Main CFD Forum | 1 | July 2, 2018 09:57 |
| Why we use finite number of Terms in Fourier Decomposition of Error in Von Neumann St | alibaig1991 | Main CFD Forum | 2 | January 26, 2018 14:46 |
| stress analysis -Von Mises Theory | watashiwa | OpenFOAM | 7 | October 15, 2010 15:43 |
| Lax method stability via von neumann analysis | morteza08 | Main CFD Forum | 1 | June 5, 2010 12:43 |
| wmake compiling Problem with OF1.5 | openTom | OpenFOAM Installation | 4 | May 3, 2009 14:44 |