 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Pavan Inguva
Join Date: Dec 2019
Location: Singapore
Posts: 7
Rep Power: 6  |
Hi!
I am trying to implement a model for a single phase flow reaction with an energy equation to model non-isothermal effects. But the formulation of the energy equation in the system is something I am trying to figure out. The model thus far: Navier-Stokes: 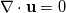 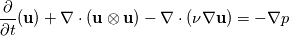 Species transport: 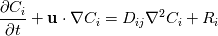 Energy Equation: This is where I am a bit unsure. I have seen a formulation energy equation that accounts a term for "energy flux by molecular diffusion" (Froment & Bischoff) which is the last term in the equation below: 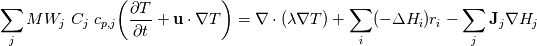 But I am more familiar with the following formulation which has 1) transient term, 2) advective term, 3) diffusive term and 4) source term which would be the heat of reaction: 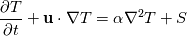 So would the additional term (energy flux by molecular diffusion) be necessary for a good model for such a reactive flow problem. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 13  |
The answer to your question depends on the problem you want to solve.
Your heat flux due to species diffusion in your energy equation is a very simple approximation of Onsager reciprocal relations, namely the Dufour effect, based on non-equilibrium thermodynamics. What problem do you want to solve? Regards
__________________
Check out my side project: A multiphysics discontinuous Galerkin framework: Youtube, Gitlab. Last edited by Eifoehn4; December 17, 2019 at 13:44. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,675
Rep Power: 66    |
The diffusion of energy is more generally written as:
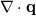 where q is a generalized diffusive energy flux. For homogeneous media, q is only heat diffusion from Fourier's law: 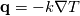 You can of course use, 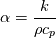 , to write it in terms of thermal diffusivity instead of thermal conductivity. For multi-component problems, there is diffusion of heat via concentration gradients, which is the last term in your equation. , to write it in terms of thermal diffusivity instead of thermal conductivity. For multi-component problems, there is diffusion of heat via concentration gradients, which is the last term in your equation.If you derive your energy equation assuming diffusion of heat is only via heat conduction/diffusion then you end up with: 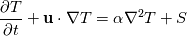 The source is a fudge factor because you didn't account for any possible chemical reactions or alternative forms of energy transport. Note that when the equation is written in this way, S is a temperature source. It's not even an energy source! If you properly derive an energy transport equation starting with conservation of total energy then you should get the more complicated looking thing you showed: 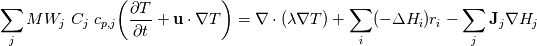 The heat of reaction is contained in the term: 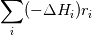 The contribution of heat diffusion via temperature gradients vs species gradients depends on the problem. If the reaction is nearly isothermal, then species diffusion will dominate. If the reaction is highly exothermic, then thermal diffusion dominates. It may also be important to mention that these are the time-accurate equations (which means you are doing DNS, whether laminar or turbulent). If you do time/Reynolds-averaging, the contribution of turbulent transport also needs to be taken into account and this gets even more wonky. Last edited by LuckyTran; December 17, 2019 at 20:17. |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Pavan Inguva
Join Date: Dec 2019
Location: Singapore
Posts: 7
Rep Power: 6  |
Thanks for your really valuable insights regarding the Dufour effects. Fortunately it seems that neglecting the Dufour effect is not a bad assumption for many cases of reacting flows.
For others' reference, I found that this book was great for outlining the derivation of the model equations and also discusses the Dufour effects with some detail: https://www.springer.com/gp/book/9783540686224. |
|
|
|

|
|
 |
| Tags |
| energy balance, reacting flows, species tranport |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Porous Modeling of Energy equation in OpenFOAM | mohammad_kordo | OpenFOAM Running, Solving & CFD | 9 | November 22, 2020 07:18 |
| Fluent do not use my velocity field(by UDF) to solve energy equation | tangleiplus | Fluent UDF and Scheme Programming | 6 | January 21, 2019 21:28 |
| Energy equation in rhoCentralFoam (revisited) | usv001 | OpenFOAM Programming & Development | 3 | July 5, 2018 05:52 |
| rhoCentralFoam: making sense of the diffusive corrector equation for energy | tatu | OpenFOAM Running, Solving & CFD | 5 | February 19, 2013 08:19 |
| how to disable energy equation for for non-newton | yueroo | FLUENT | 2 | April 3, 2001 22:11 |