 |
|
|
[Sponsors] | |||||
Intuition for why flow follows convex surfaces |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#21 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
Actually I am overthinking it. Fluids by definition fill their volumes.
If you go back to micro-kinetic theory of gases... Fluids are ensembles of many many (avogadro number) of particles with random motions. The static pressure of a fluid is simply the mean momentum of the particles that is exerted in every direction. So fluids, being fluids, have a spontaneous tendency to fill whatever volume they are placed in regardless of whether they are flowing or stagnant. This happens until there is some surface tension or other force which holds the fluid together (like gravity and the atmosphere) or the fluid encounters an obstacle (walls). Fluids are a little unlike point particles in classical mechanics. Point particles have inertia, and they continue to follow trajectories (per Newton's laws of motion) unless acted upon by external forces. Fluids only obey this in the bulk sense. So if it doesn't follow the contour of a convex surface... it's not a fluid! |
|
|
|

|
|
|
|
|
#22 | |
|
New Member
Join Date: Feb 2021
Posts: 16
Rep Power: 5  |
Quote:
I had thought of something else along the molecular lines though - general fuzzy idea: For the quasi-static explanation (#2 above), the pressure at a given location during acceleration would be related to the momentum of the gas molecules relative to bulk flow. And the transfer of momentum/pressure might be proportional to the gradient in momentum/pressure of gas molecules. So the relationship between pressure and acceleration (momentum flux) in a quasi-static fluid could be directly analogous to the relationship between temperature and heat flux. So that explains why pressure and hence velocity in quasi-static flow would develop in a potential flow pattern. ...? |
||
|
|

|
||
|
|
|
#23 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
Recirculations don't happen in potential flows because as soon as there is recirculation, there is a vorticity. Vorticity being present means that either:
1) the hand-of-God somehow reached into the flow and produced a vorticity 2) there is viscosity (1) would be mythical and (2) is what we consider a property of a non-ideal fluid. So McLean apparently has gone and interpreted this as ideal flows have no issues following convex surfaces. Regarding the what-if scenario. What if there is magically a recirculation behind my airfoil and now I blow over it. It advects downstream! The recirculation just leaves until the flow transitions to the steady solution with no recirculation. You could also do this what-if game with the heat equation. What if there is a tornado of heat initially present in my solid. Eventually it disappears. |
|
|
|

|
|
|
|
|
#24 | ||||
|
New Member
Join Date: Feb 2021
Posts: 16
Rep Power: 5  |
Quote:
Quote:
Quote:
Quote:
|
|||||
|
|

|
|||||
|
|
|
#25 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
I don’t understand the discusssion ... potential flow is a mathematical model, approximating a real flow. What are you looking for a physical intuition?
|
|
|
|

|
|
|
|
|
#26 | |
|
New Member
Join Date: Feb 2021
Posts: 16
Rep Power: 5  |
Quote:
|
||
|
|

|
||
|
|
|
#27 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
||
|
|

|
|
|
|
|
#28 | |
|
New Member
Join Date: Feb 2021
Posts: 16
Rep Power: 5  |
Quote:
Or are you saying "no one should care about getting an intuition about how fluids follow surfaces"? If so, I disagree. Or are you saying "no one should care about getting an intuition for potential flow since it's not real"? If so, I disagree. Or are you thinking "this is the wrong forum for this discussion - we do math and CFD here - not intuition"? |
||
|
|

|
||
|
|
|
#29 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
Let me do an example, potential flow around a cylinder. Observe the streamline around the cylinder, it has a constant total pressure. If the streamline would separe in the rear part to create a separation that would mean that the total pressure is changed and the flow does not mantain the same energy. But we know from the Crocco equation that the total energy must be constant in potential flow. There is no irreversibile process, the flow downstream must be specular to the flow upstream for energetic reversibiliy. Indeed you can generate lift only artificially, by generating a non-vanishing circulation with the Kutta condition, but without generating separation. This is an “intuition” associated to the math. Of course it is a consequence of the adopted mathematical model that is an approximation of the reality. |
||
|
|

|
||
|
|
|
#30 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
If you want to discuss real life, then we go to the Navier-Stokes equations and forget this potential flow and we don't need to discuss how flow separation does not occur (because it does, frequently).
In potential flows, vorticity being generated means there was an external torque being applied. I don't see a waterwheel in any of your images showing where this screw and torque would come from. If you have a vorticity generator as part of your setup then we are talking about a flow with a vorticity generator, which is something different. In your divergent channel flow that is not attached due to clever initialization there is an initial vorticity in the flow (but there still isn't a vorticity generator). If you let it flow, eventually the flow will due flowy things and all the initial vorticity will be swept away, never to be seen again. You can initialize a flow with anything you like. But an initial condition is not a guaranteed steady state solution. Last edited by LuckyTran; March 12, 2021 at 23:41. |
|
|
|

|
|
|
|
|
#31 |
|
Senior Member
|
I think the closest you can get to a physical intuition of Euler equations is by looking at how they, and NS equations, are obtained from the statistical mechanics
https://en.m.wikipedia.org/wiki/Chap...3Enskog_theory But then, that's it. NS or Euler equations already are sufficiently far away from the reality of what actually happens, not to mention potential flows or the steady temperature distribution. Thus, in my opinion, if you want to use a PDE, you can't pretend to use physical intuition alone and discard math, because at that point you already are all in with the math (If you want to formalize reality with a pde you need to speak the pde language). Potential flows, as a mathematical problem, are very well understood, and are very strict also on initial and boundary conditions, that must satisfy certain constraints that prohibit vorticity. Always. Euler equations have additional mechanisms at play that allow vorticity or even produce it. But as you are not interested in those mechanisms as you are instead on the lack of diffusion mechanisms, randomly introducing vorticity is the farthest away from reality that I can imagine. It's like taking a real flow field and suddenly make it non viscous. Some recirculations will probably stay there, some won't, but what this tells you about the physics? Ideally, you can imagine the ideal case of an inviscid flow in a straight channel with a divergent section, where at inlet you have an arbitrary number of strips at different velocity. They will each flow next to each other, each one obeying their own potential equations with given energy, and you will still see a completely attached flow, no matter how sharp the diverging angle. What this tells you, again, about the physics? |
|
|
|

|
|
|
|
|
#32 |
|
New Member
Join Date: Feb 2021
Posts: 16
Rep Power: 5  |
If anyone is confused but still interested about what I'm trying to figure out let me know and I can try to do a better job explaining. Otherwise, I suggest we "agree to disagree" about whether what I'm trying to do/learn is meaningful and achievable. Either way, please feel free to continue to contribute to the conversation if you are so inclined. Your experience and comments can help make sure I that any intuition I develop is physically and mathematically sound. Thank you for your help.
Does anyone know if a fluid parcel is bound to (moves with) a single streamtube in in an (unsteady) type II fluid? I could imagine how this could be the case, but the animation on wikipedia about streamtubes suggests otherwise. |
|
|
|

|
|
|
|
|
#33 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
|
||
|
|

|
||
|
|
|
#34 | |
|
New Member
Join Date: Feb 2021
Posts: 16
Rep Power: 5  |
Quote:
|
||
|
|

|
||
|
|
|
#35 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
in unsteady condition you can think about turbulence, do you think that would happen? A streamline will change its form in time according to the velocity field and is not a train track of parcels |
||
|
|

|
||
|
|
|
#36 |
|
New Member
NM
Join Date: Mar 2021
Posts: 3
Rep Power: 5  |
People tend to say it is the coanda effect, and it gets pushback. Doug pushes back on that idea in his book, but I don't know I agree with his assessment on the issue. You HAVE to look at the the development of the flow-field and not the resulting "steady" flow state over the wing. Think of a static wing that starts moving. As it moves, air will very initially tend to separate off the convex surface. When it does, that separation causes entrainment from the freestream. The freestream is entrained, accelerates, and creates a low pressure region between the wing and the freestream. Suddenly you have a small delta P pushing the separated jet back toward the wing. Eventually if that delta P is enough force to overcome the fluid momentum, the jet will attach. At high RE the jet has too much momentum and that force on it causes hardly any deflection so the flow never attaches. If you look at the streamline in the non-inertial frame, the momentum of the jet gives it a centrifugal component working to separate it. The pressure gradient dp/dr = pv^2/r must balance this centrifugal component. If it does, the flow stays attached. But the pressure gradient is established by that viscous entrainment. This absolutely requires viscosity, as entrainment is a viscous driven effect. When Doug says potential flows can create lift with no viscosity, he must mean from a mathematical perspective. Potential flows are a math tool to describe the freestream behavior and the pressure gradient that causes lift. But that behavior would never exist without viscous effects, plain and simple.
|
|
|
|

|
|
|
|
|
#37 |
|
New Member
Join Date: Feb 2021
Posts: 16
Rep Power: 5  |
Ok here is a more developed explanation of one of my ideas from post #19, explanation 2.
Working "Intuition" Theory For any fluid we know from the mathematics of fields that (  is velocity, not volume) is velocity, not volume)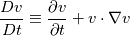 Now considering incompressible irrotational (there may be more restrictions such as constant density) fluid initialized at rest, we find for a quasi-static fluid, (which we define as 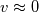 ), ),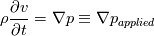 We know that incompressible irrotational fluid velocities must occur in what we will call a "potential flow pattern" at all times and so we conclude that for a quasi-static fluid the rate of change of field velocities and applied pressure gradient must also follow this pattern. I hypothesize that an intuitive explanation for the form of the applied quasi-static pressure gradient can be found by strong analogy to the way temperatures equilibrate, and that this equilibrium occurs instantaneously due to the incompressibility of the fluid. Now consider that the flow is steady but no longer quasi-static. We have 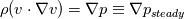 Now consider that the flow may be both unsteady and non-quasi-static. 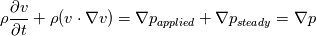 So for general flow of incompressible invsicid fluid initialized at rest we can think of the pressure field as a combination of the steady-state independent pressure field (supported by the momentum of the fluid itself) and an applied quasi-static pressure field (externally applied somehow, or due to the movement of the frame of reference from the surface itself moving). So the intuitive explanation so far is:
What's missing The big things right now are
|
|
|
|

|
|
|
|
|
#38 |
|
Senior Member
|
In order to simplify the matter, I propose to definitely assume that you are not interested in compressibility or thermal effects. So, let's just focus on unsteady potential flows and incompressible isothermal Euler equations with some vorticity either present from the beginning (doesn't matter who put it there) or from the boundary conditions. Just to avoid mentioning this every time.
Now, I am unable to discuss further the general Euler case, but just note that there is a whole inviscid instability theory that, I think, kind of treats some of the things you might be interested in. Inviscid instability theory inevitably relies on some disturbance and its evolution in an inviscid flow field. So, no disturbance no party. This has implications on the relevance of the results you get. In general, the Euler equations under the stated conditions imply the following evolution for the vorticity: 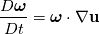 Back to potential flows, I think the picture of the pressure in the unsteady startup phase is misleading here. Because, from the equations, you have that: 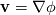 and 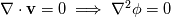 independently from time. Thus, at any single time, the potential 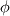 instantly adapts to its boundary conditions, doesn't matter how fast they change in time. Of course, this comes from the incompressibility assumption, but it just means that within reasonable time variations of the boundary conditions, far from the acoustic time scale, we are good to go with this. instantly adapts to its boundary conditions, doesn't matter how fast they change in time. Of course, this comes from the incompressibility assumption, but it just means that within reasonable time variations of the boundary conditions, far from the acoustic time scale, we are good to go with this.This is a very strong statement and doesn't depend from the pressure or time at all. It implies that, for given boundary conditions at a given time, there is only one way to satisfy continuity for a potential flow, and that completely determines the instantaneous velocity field. Said otherwise, a potential flow has so few degrees of freedom that the geometry of the boundaries and the boundary values completely determine it because of its mass preserving constraint. Once you know the potential/velocity from the above equation, it is the momentum equation, Newton 2nd law, momentum conservation, whatever the name, under the stated conditions, that governs how the pressure behaves. You start from here: 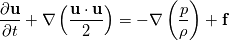 where the convective term form stems from the Lamb form and the potential assumption and 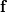 is an external force field that I now assume that can be expressed as minus the gradient of a potential is an external force field that I now assume that can be expressed as minus the gradient of a potential 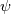 (i.e., (i.e., 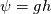 for gravity, where for gravity, where 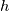 is the quote). Then you notice that all the terms are gradients of something and get (as space and time derivatives commute): is the quote). Then you notice that all the terms are gradients of something and get (as space and time derivatives commute):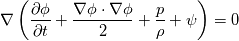 which means that the quantity in parentheses is constant in space (but might have a time dependence): 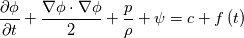 but we can also make the transformation: 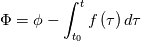 which leaves the gradient unaffected (i.e., 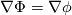 ), and finally obtain: ), and finally obtain: that finally gives the pressure as: 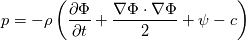 Hence, you see, under the hypotheses we used, pressure is not the cause of the motion in the way we classically understand it, it is part of a conserved quantity. Of course, in some cases, you can pretty much use the same equation to actually assign the pressure on a boundary and determine the resulting potential gradient to be used in the mass conservation equation, but that doesn't uniquely specify the potential nor is possible in general. Most importantly, it is a fact that the potential doesn't depend from the pressure. That is, it can be specified and solved for without ever recurring to the pressure, while the latter can't. If you want to analyze things from a different perspective, you can start from the momentum conservation and see that these flows conserve a quantity that, in order to also satisfy the mass conservation, has strict requirements on how one of its terms can vary in space, to the point that it is the pressure that basically follows, and not the other way around. In this picture, even if you specify the pressure at the boundary as a source of motion, it has just the effect of establishing a potential on the boundaries, but the actual pressure in the domain will still follow the conservation of mass, no matter what. EDIT: Also, note that, to a large extent, this also holds when viscosity is present because, as a matter of fact, there are several methods that allow to advance the field without ever mentioning the pressure (psi-omega and spectral methods are just two examples without getting into the details of the fractional step methods). Hence, at least for incompressible flows, the pressure always follows from a constraint on the continuity equation. So it can't be the cause of anything local. |
|
|
|

|
|
|
|
|
#39 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Paolo is addressing that the key of the discussion is that what we call "pressure" is not at all the thermodynamic pressure we usually think in our real life.
Again, the physical intuition cannot be really applied for a mathematical problem where the sound velocity is assumed to be infinite and the pressure is something different from the intuition in physics we can use. There is a clear mathematical point, for incompressible flows the only unknown is the velocity field. The "pressure" is only a lagrangian multiplier for determining the divergence-free velocity solution. And I don't see how the topic of instability can be relevant to this discussion. |
|
|
|

|
|
|
|
|
#40 | |
|
Senior Member
|
Quote:
|
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Will the results of steady state solver and transient solver be same? | carye | OpenFOAM Running, Solving & CFD | 9 | December 28, 2019 05:21 |
| mass flow through surfaces in CFD-Post | rfavalli | CFX | 2 | August 21, 2015 07:33 |
| Flow meter Design | CD adapco Group Marketing | Siemens | 3 | June 21, 2011 08:33 |
| Question on 3D potential flow | Adrin Gharakhani | Main CFD Forum | 13 | June 21, 1999 05:18 |
| computation about flow around a yawed cone | Tylor Xie | Main CFD Forum | 0 | June 9, 1999 07:33 |