 |
|
|
[Sponsors] | |||||
Intuition for why flow follows convex surfaces |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#41 |
|
Senior Member
|
It is also useful to mention that for an incompressible (i.e., constant density) flow you can't, indeed, fix a pressure boundary condition in reality. If you wanted to make an over/under pressure in some region, your only chance would be trough some imposed velocity motion, because you wouldn't be able to compress/expand the fluid in a closed reservoir.
So, in the end, as long as we assume a completely incompressible fluid as model, both the physics and mathematics of the problem tell us that pressure actually follows also for the boundary conditions. |
|
|
|

|
|
|
|
|
#42 |
|
New Member
Join Date: Feb 2021
Posts: 16
Rep Power: 5  |
I think I understand that we can determine the flow from
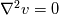 without resorting to pressure. I don't think that makes it wrong to involve a physical thermodynamic pressure in my mental model. Yes, in real life the pressure couldn't propagate instantaneously, but you have that same problem with mass conservation since real fluid is not perfectly incompressible. And I think the model could be made consistent mathematically, if necessary by doing something like allowing the fluid to be compressible and considering the limit as the compressibility went to zero. without resorting to pressure. I don't think that makes it wrong to involve a physical thermodynamic pressure in my mental model. Yes, in real life the pressure couldn't propagate instantaneously, but you have that same problem with mass conservation since real fluid is not perfectly incompressible. And I think the model could be made consistent mathematically, if necessary by doing something like allowing the fluid to be compressible and considering the limit as the compressibility went to zero.Perhaps there are ways to explain the surface-following-effect intuitively both with and without resorting to pressure. Does thinking about pressure in a causal sense and breaking it down into applied and non-applied fields (as defined in my post) introduce any inconsistencies in predicted flow pattern? Is it wrong, or does it just rub you the wrong way for philosophical and/or practical numerical reasons? |
|
|
|

|
|
|
|
|
#43 |
|
Senior Member
|
Quote:
One way to split pressure in the incompressible case is to have a background thermodynamic pressure that one can show is constant in space (but whose value might be time dependent) plus the pressure we discussed so far. As the thermodynamic part is constant in space, I don't see, again, how it enters the picture. |
|
|
|

|
|
|
|
|
#44 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
To be honest, I was unable to understand the physical intuition in your previous post. As I addressed some post ago, you missed totally the energetic part of the question. A streamline in potential flow remains associated to a constant total pressure. That means that kinetic energy is converted in a reversible way. By an energetic point of view, you can see the flow over a cylinder as same way either from the left or the right sides. Any hypothesis of separation should be constrained by the conservation of total enthalpy. Crocco showed the way. And that is not possible. |
|
|
|

|
|
|
|
|
#45 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
Just to reiterate some points:
Viscosity and compressibility do not need to be considered because these are resistances to fluid deformation. These phenomenon explain why the flow would refuse to follow contours of negative curvature. Neglecting them and considering ideal potential flows, helps us to appreciate that the flow has spontaneous desires to follow convex surfaces. Real fluids and real flows of course have these properties, but if we're interested in why ideal fluids do what they do, it makes sense to neglect the things that we want to neglect. In ideal flows, pressure is whatever it needs to be for the fluid to flow the way it wants to flow. For incompressibe flows, due to disconnection between thermodynamic and flowing pressure, there is also no upper limit on what the pressure can be. This is of course just a corollary to: pressure is whatever it needs to be. The irrotationality constraint limits the flow to certain types (in our discussion that means separation doesn't happen). If you consider structural mechanics etc., you will find that the walls of the vessel do indeed apply a net force onto the fluid. So eventually something does indeed need to exert pressure for the flow to flow the way it does. But that takes us back to the question: so why does it flow this way to begin with? There are tons of mathematical and physical theorems that explain these: principle of least action, path of least resistance, etc. But keep in mind these are consequences of mass conservation law and laws of motion. I feel like one person here is trying to mathematically prove the natural laws of the universe.  If one could explain a natural law... that would be quite an achievement. If one could explain a natural law... that would be quite an achievement.
|
|
|
|

|
|
|
|
|
#46 |
|
New Member
Join Date: Feb 2021
Posts: 16
Rep Power: 5  |
I might give this thread some time off and see if someone like-minded comes along and wants to contribute some ideas or re-initiate the conversation. See edit on the very first post.
|
|
|
|

|
|
|
|
|
#47 |
|
Member
james nathman
Join Date: May 2011
Posts: 62
Rep Power: 15  |
Another example of potential flow modeling separation is a body of revolution at angle of attack. The hull of the USS Akron airship was analyzed at 16 degrees angle of attack. Attached flow produces zero lift. A crossflow separation calculation produces the location of separation. A shear layer is then attached at the separation location. The geometry and strength of the shear layer is determined as part of the panel-method solution. The error in lift is reduced from 100% to 5%.
The figures display the pressure distribution on the body. Blue is stagnation, red is the suction end of the scale. The filaments show the geometry of the shear layer. Many panel-method implementations don't allow wakes (shear layers) to be attached at the separation location. The stream function cannot be applied to this 3-D case. |
|
|
|

|
|
|
|
|
#48 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
Actually, the stream function-vorticity formulation can be applied also in this 3D case! Just consider the vector potential field. |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Will the results of steady state solver and transient solver be same? | carye | OpenFOAM Running, Solving & CFD | 9 | December 28, 2019 05:21 |
| mass flow through surfaces in CFD-Post | rfavalli | CFX | 2 | August 21, 2015 07:33 |
| Flow meter Design | CD adapco Group Marketing | Siemens | 3 | June 21, 2011 08:33 |
| Question on 3D potential flow | Adrin Gharakhani | Main CFD Forum | 13 | June 21, 1999 05:18 |
| computation about flow around a yawed cone | Tylor Xie | Main CFD Forum | 0 | June 9, 1999 07:33 |