[FMDenaro]

Originally Posted by MardyOwens

I have just: Large Eddy simulation for Incompressible fluid of Sagaut.

I also have the book of Pope.


Are there others?

There are also further textbooks but you will be ok reading these two.

[MardyOwens]

I have read during this week.
I still have some questions regarding the implicit filter.
How the Sub-Grid Scale Model can act as an additional filter??

The papers that I read regarding this, do not represents spectra, so it is difficult to understand how they act as filter. I always thought that the sub-Grid Scale Model act after pi/Delta . Can you give me a hint regarding this?

[FMDenaro]

Originally Posted by MardyOwens

I have read during this week.
I still have some questions regarding the implicit filter.
How the Sub-Grid Scale Model can act as an additional filter??

The papers that I read regarding this, do not represents spectra, so it is difficult to understand how they act as filter. I always thought that the sub-Grid Scale Model act after pi/Delta . Can you give me a hint regarding this?

Be careful ... the SGS model mimics the contribution of the unresolved terms (for k>pi/h) but its action is to add a contribution to the resolved ones (k<pi/h). Generally, this contribution is in terms of an energy dissipation, like a further filtering. But from a rigorous point of view the SGS is not a filtering

[MardyOwens]

Originally Posted by FMDenaro

Be careful ... the SGS model mimics the contribution of the unresolved terms (for k>pi/h) but its action is to add a contribution to the resolved ones (k<pi/h). Generally, this contribution is in terms of an energy dissipation, like a further filtering. But from a rigorous point of view the SGS is not a filtering

Do you have references for this? I am struggling to find them

[sbaffini]

Originally Posted by MardyOwens

I have read during this week.
I still have some questions regarding the implicit filter.
How the Sub-Grid Scale Model can act as an additional filter??

The papers that I read regarding this, do not represents spectra, so it is difficult to understand how they act as filter. I always thought that the sub-Grid Scale Model act after pi/Delta . Can you give me a hint regarding this?

It is actually simpler than you think.

First of all, let me distinguish the Sub Grid Scale (SGS) models from the Sub Filter Scale (SFS) models. As you mentioned, the former are meant to represent contributions from scales below the grid but, if you think about it, when you use them, you are doing it on your grid, not a finer one, so they necessarily act on your solved scales. SFS models, which are meant to represent interactions explicitly involving the resolved scales, by the same reasoning also act on the solved scales. Basically, whatever you add to your equations, necessarily acts on the solved scales, but may be meant to represent things happening at some other scale, represented or not.

Now, SGS models are typically in the form of an added dissipative term. More specifically, a larger viscosity. If you have an idea of how spectra change when Re is lowered, it should be pretty clear why a SGS model acts as an additional filter. Another way to look at it is by considering how a typical filter would act:



Then you can rearrange this into: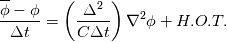



So filtering is like advancing your solution with an artificial viscosity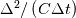

Now, I cannot speak for all the SFS models, but in the FV framework, when properly formulated without commutation errors, turns out that including a scale similar model also for the diffusive term is equivalent, at the lowest order, to the inclusion of an hyperdissipative term (i.e., 4th order Laplacian), something similar to the Rhie-Chow term if you know it (which indeed appears in the pressure equation if you include a scale similar pressure term as well).

Now, this might be less obvious but, in fact, any even order derivative term would act as a filter. The higher the order, the more the filter would resemble a spectral cut off one. So a 4-th order Laplacian as implied by a proper scale similar model in the FV context would still imply, at the lowest order, an additional dissipative filter (just more compact than the one implied by the SGS model). I speak of lowest order because such reasoning is based on expanding the model in a Taylor series (something that was not necessary for the SGS model to reason about it).

For the convective scale similar term however, which is more common, things are more complex and this is not obviously true in general (otherwise simple dissipative models would work much better). Nonetheless, there is at least one SFS LES approach, the approximate deconvolution modeling approach (ADM) that, in one of its formulations (due to Mathew) can be rearranged into just an high order explicit filtering of the equations (higher than a fourth order Laplacian). So, again, SGS modeling is reduced to filtering (in fact there are indeed additional LES formulation that just require high order filtering).

[FMDenaro]

Originally Posted by MardyOwens

Do you have references for this? I am struggling to find them

You cannot find this specific sentence in the literature, what I wrote above is implied in the LES philosophy, since from its origin. The SGS adopts the filtered field, therefore the results acts only on the filtered field. In no way you can add components outside pi/h.

[FMDenaro]

Originally Posted by MardyOwens

Do you have references for this? I am struggling to find them

You could find useful a reading of my lectures on LES, the .ppt files are on my RG page. You can find also some references.