 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
N/A
Join Date: Feb 2021
Posts: 22
Rep Power: 5  |
Dear Users,
I am doing some research about the Large Eddy simulation. I found some apparent discrepency in the definition of the filter G between the paper of two authors (but I found a lot of other paper with different definitions as well). I have attached both, the paper are: Leonard, A. (1975). Energy Cascade in Large-Eddy Simulations of Turbulent Fluid Flows. Advances in Geophysics, 237–248. doi:10.1016/s0065-2687(08)60464-1 Piomelli U. 2014 Large eddy simulations in 2030 and beyond. Phil. Trans. R. Soc. A 372: 20130320. http://dx.doi.org/10.1098/rsta.2013.0320 In both I didn't understand what they intend for the variables x and x', and why they are in bold. Why the function of Piomelli depends on delta and the one of Leonard does not? Last Question: If the filter is implied, how does G become? |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
x is your traditional position. x' is a dummy position variable inside the integral (integrating over the entire domain is the filtering operation).
At a high-level, it doesn't really matter that one depends on x-x' and the other on delta. All that matters is that there is a filter function G, and applying the filtering operation to f(anything) over the entire domain gives you a filtered f with an overbar. I.e., they could just as easily write G(x,x',delta), G(x,x'), G(x-x'), or just G or any other letter, say H. We haven't said what are the details of the filter G yet. And until we do, it could be anything. G(something) is some filter function that makes the LES act like LES. |
|
|
|

|
|
|
|
|
#3 | |
|
New Member
N/A
Join Date: Feb 2021
Posts: 22
Rep Power: 5  |
Quote:
|
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Bold symbols are always for vectors, a capital letter stands for tensors.
Delta is a parameter, not a variable, it is the width of the filter. To understand better, this is an example of the top hat filter (1D) f_filt(x; Delta)= (1/Delta) Int[x-Delta/2;x+Delta/2] f(x') dx' Be aware that different authors can use different notations. |
|
|
|

|
|
|
|
|
#5 | |
|
New Member
N/A
Join Date: Feb 2021
Posts: 22
Rep Power: 5  |
Quote:
|
||
|
|

|
||
|
|
|
#6 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
Well, when LES is performed using an implicit filter, then G is the filter function implied by the type of discretization. For example, a spectral method implies a Fourier cut-off filter, a finite volume method implies an approximation of the top-hat filter. The exact shape of the implicit filter is strongly depending on the discretization... |
||
|
|

|
||
|
|
|
#7 | |
|
New Member
N/A
Join Date: Feb 2021
Posts: 22
Rep Power: 5  |
Quote:
|
||
|
|

|
||
|
|
|
#8 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
https://www.researchgate.net/publica...dy_Simulations |
||
|
|

|
||
|
|
|
#9 | |
|
Senior Member
luca mirtanini
Join Date: Apr 2018
Posts: 165
Rep Power: 8  |
Quote:
You use the same formalism in the Eq. (2) of your article (the schumann approach). I though that this formalism meant that the filter is implied, because if compared with the Eq. (1), it seems that G is 1/Delta^3 . Which is the Schumann paper you are referring to? Why eq. (1) becomes eq.(3)? |
||
|
|

|
||
|
|
|
#10 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
There is a lot of confusion in this topic... When using a FVM, you discretize the integral equations, therefore the volume averaging corresponds to the filter operation. However, this operation is never really applied, the volume-averaged (filtered) variable is a conseguence of the fluxes reconstruction. On the other hand, using a FDM you dicretize the differential equations and the filter is hidden in the type of discretization of the derivatives. For all method, the grid finally acts as a cut-off filter at the Nyquist frequency. The real value of the filter width Delta is not exactly a user choice but depends on the discretization. The Schumann paper is old, he did not analysed such issues in implicit filtering. In my paper you can see the Eq.(5) as a filter equation in a FVM |
||
|
|

|
||
|
|
|
#11 | |
|
New Member
N/A
Join Date: Feb 2021
Posts: 22
Rep Power: 5  |
Quote:
Thank you for your explanation. Maybe I am trying to understand. Indeed I cannot understand how is it possible to go from eq. (1) to eq. (2). Where does it go the G function? |
||
|
|

|
||
|
|
|
#12 |
|
Senior Member
|
Please, allow me to add that:
1) 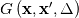 means that the filter has an explicit dependence on the spatial coordinate means that the filter has an explicit dependence on the spatial coordinate 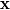 . This might both refer to a spatial variability of . This might both refer to a spatial variability of  and to a general variabilty of the filter kernel support, higher order moments, etc. and to a general variabilty of the filter kernel support, higher order moments, etc.2)  means that the filter only depends from the distance between the integration point and the physical coordinate. In this case one can formally refer to the operation as a convolution. More importantly, one can show that this form of filter commutes with spatial derivatives. means that the filter only depends from the distance between the integration point and the physical coordinate. In this case one can formally refer to the operation as a convolution. More importantly, one can show that this form of filter commutes with spatial derivatives.While the Schumann form was more common in the early LES age, today it is largely wrong to keep assuming that the filter has no spatial dependence and one should recognize the Piomelli form as the one always in place, recognized or not by the author. For what concerns the implicit filter, one can use the formalism of the weighted residual method to show what the implied filter is in most numerical discretizations (my Ph.D. thesis has a section on it). Some numerical schemes, however, add additional difficulties in the interpretation of the solution as one obtianed under one single filter. What formalisms can't really do (nor any model in itself) is quantifying/qualifying the rich SGS dynamics hidden in  terms taken away by the grid. terms taken away by the grid.
|
|
|
|

|
|
|
|
|
#13 | |
|
New Member
N/A
Join Date: Feb 2021
Posts: 22
Rep Power: 5  |
Quote:
Thank you! I was searching something like your thesis. Congratulations, the reference work is amazing. |
||
|
|

|
||
|
|
|
#14 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
For example, considering the top-hat filter, G=1/Delta in the interval x-Delta/2;x+Delta/2 and zero elsewhere. In practices you have the definition of a local cell-averaging |
||
|
|

|
||
|
|
|
#15 | |
|
New Member
N/A
Join Date: Feb 2021
Posts: 22
Rep Power: 5  |
Quote:
When you say "the formalism of the weighted residual method to show what the implied filter is in most numerical discretizations", which equation are you meaning? |
||
|
|

|
||
|
|
|
#16 | |
|
Senior Member
|
Quote:
Now, since then, and before my thesis, several people have formalized filters and filtering operations, including those related to implicit filters. Filippo worked on the finite volume ones. Others worked on the others (they are all mentioned in the thesis). What, I think, I have done in my thesis is taking the formalism already devised by Filippo for finite volumes, make it slightly more general, take the formalism of the weighted residuals method (wrm) and show that the two are exactly the same and that the same conclusion can be drawn for all the others (section 3.6.3 of the thesis). What the wrm specifically allows to say is that: 1) Most numerical methods (finite differences, volumes and elements, spectral methods) can be formalized under the same method. 2) This general all-inclusive method solves, independently from the details of the specific method, for a filtered variable. The details of the filter of course change from method to method. 3) The equations that are solved by this general all-inclusive method are themselves filtered equations, under the same filter of point 2 above. All of this was basically already figured out by Vreman as well in his 2004 paper, but I like to think that I figured a more elegant, pedestrian level, way of presenting it. So, to answer your question, using the wrm formalism I can show in equations 3.45 and 3.47 that a finite volume solution can be interpreted as a combination of a top-hat filter followed by a grid sampling, in this very specific order. This, of course, doesn't tell the whole truth about implicit filtering as numerical discretizations on finite grids would add additional implicit filtering, but the formalism allows to separate them (also in lieu of a possible future treatment) from what the discrete approach implies by itself, independently from the numerical accuracy. So, yes, in these terms, the implicit filter can be totally qualified but to become explicit and practical, for example, in the case of the finite volume solution it requires to know how you assume the FV solution to vary from a cell center to the other (the phi in equation 3.45). |
||
|
|

|
||
|
|
|
#17 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
And that is a further topic, still object of discussions in literature (see for example the recent papers of Nishikawa) |
||
|
|

|
||
|
|
|
#18 |
|
New Member
N/A
Join Date: Feb 2021
Posts: 22
Rep Power: 5  |
||
|
|

|
|
|
|
|
#19 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
||
|
|

|
|
|
|
|
#20 |
|
New Member
N/A
Join Date: Feb 2021
Posts: 22
Rep Power: 5  |
||
|
|

|
|
 |
| Tags |
| filter, les filter |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Principal variable in energy equation is total enthalpy or total internal energy? | lostking18 | CFX | 3 | June 11, 2019 01:20 |
| Filtered navier stokes equation..LES:: | Palani Velladurai | Main CFD Forum | 7 | September 6, 2013 02:51 |
| Constant velocity of the material | Sas | CFX | 15 | July 13, 2010 08:56 |
| CFX Additional Variable Transport Equation | Scott Nordsen | CFX | 3 | January 30, 2010 05:36 |
| Additional Variable - Diffusive Transport Equation | RadheShyam Das | CFX | 3 | October 18, 2007 12:35 |