 |
|
|
[Sponsors] | |||||
What does the Boussinesq eddy viscosity hypothesis really means? |
 9Likes
9Likes
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Songrui LI
Join Date: Jul 2022
Location: shanghai
Posts: 3
Rep Power: 4  |
Hi CFDers
I just stepped into the mathematics of the RANS model and I got stuck. When I read the Boussinesq hypothesis, also called the eddy viscosity hypothesis, I saw this equation and the name of every term. Such as 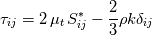 where 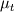 denotes the eddy viscosity, denotes the eddy viscosity, 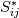 the strain rate tensor and the strain rate tensor and 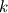 the turbulent kinetic energy. the turbulent kinetic energy. But I still have concerns, After some research, here are what I know so far: the strain rate tensor describes the rate of change of the deformation of the fluid in the neighborhood of a certain point. The turbulent momentum transfer results in the deformation of the fluid, and the deformation gives rise to viscous forces in its interior against the deformation, due to friction between adjacent fluid elements, and due to the internal stress tensor. And the turbulent kinetic energy defines the energy of motion carried by fluid flow. And it dissipates down the turbulence energy cascade. Here are what I still don't know: Why the kinetic energy term in the above equation? I don't know how the turbulent kinetic energy is related to the stress tensor. Why 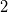 and and  in the above equation? I don't know whether this is pure empirical or if there is a theory behind these factors. in the above equation? I don't know whether this is pure empirical or if there is a theory behind these factors.Thank you |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
I suggest you to think about the decomposition of the tensor in isotropic and deviatoric parts. You will see the 1/3 appearing. The model is for the deviatoric part of the stress, thus the isotropic part will be added to the pressure. The 2 appears exactly as in in the molecular diffusion term. |
||
|
|

|
||
|
|
|
#4 | |
|
New Member
Xingguang Zhou
Join Date: May 2022
Location: CHINA
Posts: 14
Rep Power: 4  |
Quote:
About the coefficient 2/3, this is from the average of turbulent kinematic energy. Actually here is Pt, a "pressure" due to fluctuating velocity. Best Regards. |
||
|
|

|
||
|
|
|
#5 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
Really it's about understanding where the 3 in 1/3 comes from. If you're asking why 2, then look at the definition of S and tell me why there is a 1/2 in it.
|
|
|
|

|
|
|
|
|
#6 | |
|
New Member
Songrui LI
Join Date: Jul 2022
Location: shanghai
Posts: 3
Rep Power: 4  |
Quote:
I followed your lead and I found this section demonstrates what you say and it really helps me. https://en.wikipedia.org/wiki/Viscou...viscous_stress |
||
|
|

|
||
|
|
|
#7 |
|
New Member
Songrui LI
Join Date: Jul 2022
Location: shanghai
Posts: 3
Rep Power: 4  |
||
|
|

|
|
|
|
|
#8 |
|
Senior Member
|
No, please, don't go into linear algebra, just, literally, take the trace of both sides, which are 3x3 tensors, so just take the sum of their 3 diagonal terms and take note of the definitions of all the terms
|
|
|
|

|
|
 |
| Tags |
| turbulence modeling |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Boussinesq eddy viscosity hypothesis in cylindrical coordinates? | LuckyTran | Main CFD Forum | 5 | August 12, 2015 09:28 |
| Very low eddy viscosity value in turbulent flow | mejahan | CFX | 14 | February 3, 2015 15:55 |
| Eddy viscosity ratio in interDyMFoam? | wavemaster | OpenFOAM Running, Solving & CFD | 1 | March 9, 2014 03:57 |
| Calculating Eddy Viscosity in order to visualize at Post-Processing. | RTom | OpenFOAM Pre-Processing | 0 | September 4, 2013 14:43 |
| Eddy viscosity hypothesis versus Reynolds stress models | JuPa | ANSYS | 0 | August 12, 2013 06:20 |