 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
William
Join Date: Sep 2022
Posts: 8
Rep Power: 3  |
I am wondering that when we derived the momentum equation using the differential form of the transport equation,
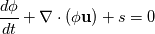 , and substituted , and substituted 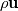 for for  , we get a term that looks like , we get a term that looks like 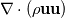 . How do we know we should use tensor product between the two . How do we know we should use tensor product between the two 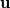 , instead of say cross product or dot product? I know that the term will only have the correct shape (i.e. it has to be a vector after taking the divergence so that it can be added to other terms in the equation), but is there a physical meaning behind the tensor product? Thank you! , instead of say cross product or dot product? I know that the term will only have the correct shape (i.e. it has to be a vector after taking the divergence so that it can be added to other terms in the equation), but is there a physical meaning behind the tensor product? Thank you!
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,675
Rep Power: 66    |
Well yes the tell is that it must be a tensor and not a vector or scalar, which immediately eliminates the possibility of a cross or inner product. Even compilers will know not to compile a sequence that has mismatched operands and throw an error if the classes are incorrect, there's no reason an intelligent human being cannot do better.
Obviously it is better if everything comes with a dictionary and a manual of how to do it. But outer and inner products already have their notations. It would be a little silly not to use them. For example in a polynomial equation ab = c, how do you know ab is the product of a and b and not addition of a and b, a+ b? Is it because you seek a higher authority to decide things for you? Or is it because addition already has a notation a+b and if you wanted it to signify addition, you would write a + b and not ab? Dyadic notation is extension of vector notation into dyadics and specifically here you are use nabla vector notation where those have clear conventions for the dot and cross products (i.e. 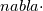 already implies dot operator being applied so why would you ignore this convention in the very next symbol already implies dot operator being applied so why would you ignore this convention in the very next symbol 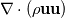 ). ).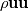 are your transport rates. They are the x,y,z (i,j,k) components of momentum transported by the x,y,z(i,j,k) components of the mass flux. are your transport rates. They are the x,y,z (i,j,k) components of momentum transported by the x,y,z(i,j,k) components of the mass flux.
Last edited by LuckyTran; September 9, 2022 at 00:55. |
|
|
|

|
|
|
|
|
#3 |
|
New Member
William
Join Date: Sep 2022
Posts: 8
Rep Power: 3  |
Apart from your unprofessionalism I think you missed the point of my question, and perhaps I did not make it very clear so my apology.
I guess a better way to phrase my question is this: the dummy property  in the transport equation can be both scalar and vector, or even higher order tensors. If it is a scalar quantity, then the operation between in the transport equation can be both scalar and vector, or even higher order tensors. If it is a scalar quantity, then the operation between  and and  is very clear and without ambiguity. However, if is very clear and without ambiguity. However, if  is now a vector quantity, the definition of the same operation is ambiguous, because there are more than one type of vector product. My source of the derivation of the transport equation did not make it clear how to interpret such an operation, but went straight ahead using the tensor product, and thus arises my question. is now a vector quantity, the definition of the same operation is ambiguous, because there are more than one type of vector product. My source of the derivation of the transport equation did not make it clear how to interpret such an operation, but went straight ahead using the tensor product, and thus arises my question.
|
|
|
|

|
|
|
|
|
#4 |
|
New Member
William
Join Date: Sep 2022
Posts: 8
Rep Power: 3  |
I think after a bit of thought I can answer this question myself now. Basically if
 is a vector quantity, then the transport equation is applied to every element of the vector individually. So for example if is a vector quantity, then the transport equation is applied to every element of the vector individually. So for example if  is a 2x1 vector, then there will be 2 transport equations, one for is a 2x1 vector, then there will be 2 transport equations, one for 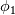 and one for and one for 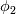 . In order to keep things compact and not having to write multiple equations, using the tensor product will yield exactly the same system of equations in vector form, eliminating the need for multi-lined, system of equations. . In order to keep things compact and not having to write multiple equations, using the tensor product will yield exactly the same system of equations in vector form, eliminating the need for multi-lined, system of equations.
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,675
Rep Power: 66    |
Now do it for the triple products and quadruple products and higher order products. If the uu is not a dyadic product then you'll a growing number of notations in order to determine if it is the inner product, double inner product, triple inner product, double outer product, triple outer product, and so on. The point of notational conventions, is actually following them. That's why they're conventions.
Also note that the dyadic product is a subclass of tensor products and it is wrong in general to call it a tensor product. It works for navier-stokes because the velocity vector is rank 1 and uu actually is a dyadic product. |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,769
Rep Power: 71    |
Quote:
|
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
|
What Lucky was probably trying to convey is that you are using your source material wrong or it is wrong the material itself.
If you were using the Einstein notation, you would have 0 doubt about everything. So, in Lucky terms, it is your impression (or a problem in the material you are reading) that the operation is subject to interpretation, but it actually isn't. To be more precise, where would a cross or dot product come from? They are simply not there. |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,769
Rep Power: 71    |
The meaning of phi is always related to the transport theorem. Any quantity phi is advected by normal component of the mass flux rho u. Consequently no scalar product can appear since
Int[S] rho un phi dS is the meaningful physical contribution. For the mass phi=1, for the momentum phi=u. |
|
|
|

|
|
 |
| Tags |
| momentum equation, navier stokes equation, tensor product |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| add a pressure drop term in the momentum equation | a.lone | FLUENT | 0 | July 3, 2019 06:48 |
| Domain Reference Pressure and mass flow inlet boundary | AdidaKK | CFX | 75 | August 20, 2018 05:37 |
| mass flow in is not equal to mass flow out | saii | CFX | 12 | March 19, 2018 05:21 |
| Coefficients discretized momentum equation | michujo | Main CFD Forum | 4 | June 20, 2012 01:33 |
| Discretization of momentum equation query | siw | CFX | 0 | June 20, 2011 08:38 |