 |
|
|
[Sponsors] | |||||
|
|
|
#21 |
|
Senior Member
|
I'm all but an expert in this field but, as a practictioner in need of a positivity preserving scheme, I gathered the following information:
1) A 1D, first order positively preserving scheme can be made nD and high order (EDIT: I now see this is similar to a work you already cited, so you probably know this as well) https://deepblue.lib.umich.edu/bitst...pdf?sequence=1 2) The scheme that Einfeldt defines as HLLEM in "On Godunov-type methods near low densities" is proven by himself to be positively preserving and has been later used as a basis for a positivity preserving entropy fix for a Roe scheme, e.g., https://perso.ensta-paris.fr/~pelant...nti_oxford.pdf Altough, I see there might be misalignment in nomenclature across references 3) My personal experience is with a preconditioned Roe scheme using an entropy fix based on the preconditioned HLLE+ scheme https://arc.aiaa.org/doi/10.2514/1.12176 and it is positivity preserving at 2nd order for a shock tube on an unstructured grid (that is, an actual 3D tube with a finite cross section). Of course, a working limiter is needed here. May I suggest you to use the very test in the Einfeldt paper to check your scheme? |
|
|
|

|
|
|
|
|
#22 | |
|
New Member
Davide
Join Date: Apr 2023
Posts: 10
Rep Power: 3  |
Quote:
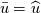 while the HLLEM scheme does not use the Roe average for the contact discontinuity velocity. while the HLLEM scheme does not use the Roe average for the contact discontinuity velocity. However in the paper I followed originally: https://www.sciencedirect.com/scienc...092?via%3Dihub (page 3) it uses the Roe averages. Anyway I will try Einfeldt test to see what happens |
||
|
|

|
||
|
|
|
#23 | |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Quote:
I have also testest the Hurrican example, the high speed example, with reconstruction (TVD, MINMOD) + Rusanov and even HLLC and had no problems. Your video seems unsymmetric, the solution should be symmetric. |
||
|
|

|
||
|
|
|
#24 |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
May i ask, how much is lowest density you are running into?
|
|
|
|

|
|
|
|
|
#25 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
||
|
|

|
|
|
|
|
#26 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
Quote:
Thank you. I was just curious. I actually have worked on cases with very low density and I decided against Riemann type solvers. I decided to go pressure based solver route. With that in my case i could go as low as 1E-5 without any problems, and i can go till 1E-7 if i push it. |
||
|
|

|
||
|
|
|
#27 | |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Quote:
We should keep in mind, that the example is designed in such a way, that it contains a physical singularity in the center (vaccum point). Every consistent, convergent and positivy preserving solver should reach a density of  without much effort (under mesh refinement) until round-off errors come into play. without much effort (under mesh refinement) until round-off errors come into play.The validity of the Euler Equations under very high Knudsen numbers is a different topic. |
||
|
|

|
||
|
|
|
#28 |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
Quote:
Can you point out which test you are talking about. Sorry a lot going on in this thread so for me hard to keep track. I can try with pressure based solver and see what happens. I expect it to break down too but things can't improve if they don't break. |
|
|
|

|
|
|
|
|
#29 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
The numbers are given for the hurricane example, reference [4], see the previous answers.
|
|
|
|

|
|
|
|
|
#30 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
I am not an expert with plasma physics and I never worked on your problem but I would ask you how do you get the Poisson equations for phi from the second equation, what are the BC.s you prescribed and how do you solve. If I understand correctly, the solved function is a "source" term in the energy (third equation). What is more, did you evaluate if you have a stiff hyperbolic problem due to the coupling? |
||
|
|

|
||
|
|
|
#31 | |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Quote:
|
||
|
|

|
||
|
|
|
#32 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
From application of the divergence operator on the second equation ? What about the BCs and the discretization of the Poisson problem? |
||
|
|

|
||
|
|
|
#33 | |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Quote:
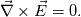 The boundary conditions and discretization may be choosen independantly. |
||
|
|

|
||
|
|
|
#34 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Quote:
Could you please better detail? I mean, apply the divergence operator to the second equation and write down the Neumann BCs. Is that sufficient to ensure the compatibility condition for the existance of a solution? |
||
|
|

|
||
|
|
|
#35 | |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Quote:
You may solve the compressible Euler-Maxwell or Euler-Poisson equation in a pressure based fashion rather than a density based fashion. In this case you would end up with an additional Poisson like equation, however for pressure, including additional source terms. Except external forces, there should be no difference to handle BCs in order to fullfill the compatibility condition for pressure. The former electro-static Poisson equation should of course also satisfy the compatibilty condition in order to be unique. |
||
|
|

|
||
|
|
|
#36 |
|
New Member
Davide
Join Date: Apr 2023
Posts: 10
Rep Power: 3  |
Hi everyone, sorry for not replying for a while.
Eifoehn4 is right, the system comes from the Euler-Maxwell in the electrostatic limit. In my case boundary conditions for Poisson are simple dirichlet. In my specific problem I got number densities as low as 0.7 m^-3 while other regions of the domain are at 10^15, so very low. It turns out that even with a more diffusive scheme sometimes the simulation fails, in particular when I have a sudden diffusion of density that expands in the low density region. This creates a non physical shock with extreme temperatures (to reproduce the problem try to do a free expansion in quasi-vacuum). In order to avoid this I decided to try another approach and coded a "vacuum tracking" algorithm which follows the interface between absolute vacuum (just 0 ) and solves Riemann problems with vacuum. This works fine especially in the free expansion case since the approximate/exact riemann solution is available (see Munz 1994), however once I have source terms, such as magnetic confinement ecc, it is not anymore free expansion and I think I have to modify the riemann solution to account for this. In particular I guess I have to remove the rarefaction wave since nothing can expand beyond the magnetic line (free expansion always assumes a rarefaction wave at the interface, being the contact discontinuity impossible to obtain due to the pressure gradient). I am not really sure on how to modify the flux function to account for this but I will look into it. I never thought of using pressure based solver, I honestly know only the one like Piso or Simple, but I always skip them for this kind of problems. Might be due to the fact that I studied on LeVeque and he just goes with Riemann problems. I will look into them as well, thanks |
|
|
|

|
|
|
|
|
#37 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
Please check the Toro's book as that is the only book that kind of talk about Riemann solvers with Vacuum.
I thought about the appraoch you talk about detecting Vacuum and this is why i was reading the Toro's book for it. The major reason why I gave up on Riemann solver was that i had a calculation with Vacuum pump (2 phase flow) and Riemann solver did not give me good flow profile in rotating geometry while pressure based solver did give me good profile. In this pump low pressures are generated so was exploring the idea of detecting vacuum and then going forward with modifying Riemann solver. The unreliability of the Riemann solver made me give up on it. I point out that the solver was validated for standard test problem so it was not inaccurate just that when rotation was involved things did not add up. I actually wrote the Riemann solver in long double precision because of low densities involved. Anyway keep us updated and also check the Toro's book. I do work on same problem actually and will be spending next 2 to 3 weeks on it (i resume where i left off). I have electron transport and now i will add ion transport with it. Quote:
|
||
|
|

|
||
|
|
|
#38 | |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Quote:
|
||
|
|

|
||
|
|
|
#39 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,278
Rep Power: 34   |
Quote:
Thank you. I will check it once i have some time to spare. I used hllc in that sim. |
||
|
|

|
||
 |
| Tags |
| euler, plasma, vacuum |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Solving coupled scalar transport equations in openFoam | pavaninguva | OpenFOAM Running, Solving & CFD | 1 | December 28, 2019 08:28 |
| Calculation of the Governing Equations | Mihail | CFX | 7 | September 7, 2014 06:27 |
| Riemann invariants of adjoint equations of shallow water equations | zqb0929 | Main CFD Forum | 0 | March 15, 2012 00:54 |
| CFD governing equations | m.gos | Main CFD Forum | 0 | April 30, 2011 14:21 |
| ? fluctuating equations for homogenous shear turb. | ff_fan | Main CFD Forum | 1 | September 20, 2002 07:39 |