 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
Join Date: Apr 2009
Posts: 118
Rep Power: 17  |
I have seen a number of forum posts on this topic but I'm still struggling with my boundary conditions.
I'm running a 1-D spherical calculation (only radial dependence considered). I decided to have velocity boundary conditions at the inlet and outlet. So the BCs I have are: inlet: 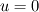 outlet: 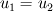 which is zero gradient BC. which is zero gradient BC.I understand that for subsonic simulations you either have to specify velocity or pressure BCs. I have a staggered grid where the velocities are staggered forward. My discretised equation for the pressure looks of the form 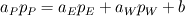 I used the discretised equation to calculate the pressure values at the boundary. At the inlet since I have 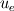 therefore, I do not have therefore, I do not have 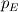 in the discretised pressure equation and for the outlet I do not have in the discretised pressure equation and for the outlet I do not have 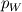 . Is this correct? . Is this correct?
|
|
|
|

|
|
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Impinging Jet Boundary Conditions | Anindya | Main CFD Forum | 25 | February 27, 2016 12:58 |
| [Gmsh] Import problem | ARC | OpenFOAM Meshing & Mesh Conversion | 0 | February 27, 2010 10:56 |
| Fluent accuracy and boundary conditions | Paolo Lampitella | FLUENT | 0 | June 12, 2008 06:25 |
| Pressure boundary conditions | Lionel S. | Main CFD Forum | 1 | August 24, 2007 18:03 |
| A problem about setting boundary conditions | lyang | Main CFD Forum | 0 | September 19, 1999 18:29 |