Erroneous pressure profile at the boundary cells (1D case)

Saideep · February 25, 2020, 11:47

Hi,

I am trying to solve the following Laplacian equation in a 1D channel:

Code:

fvm::laplacian(var, p)

where 'var' is a variable computed before solving this equation.

I use a fixedValue boundary condition (inlet/ outlet) for pressure and zeroGradient boundary condition for velocity.

When I run the case, I notice that pressure at the boundary cells (inlet, outlet) are not accurate which show a larger slope (which shall not happen). See, Fig. 1 (near the inlet), Fig 2 (near the inlet), Fig. 3 (near the inlet and outlet). As, a consequence the flux computed is not accurate. At the end of the run (Fig. 3), I loose a subtantial amount of pressure gradient due to this artefact and my flow velocity is much slower that what shall actually be. In reality, the pressure profile in Fig. 3 must be a straight line (with constant slope) connecting 70 Pa near inlet and 0 Pa near outlet.

I tried refining the mesh, time step and different numerical solvers, schemes but could not solve the issue. In short, the pressure is happy to convergence to a wrong value at the boundaries and this happens in only 1 iteration (I reach a residual of e-20 in 1 iteration).

Any hints on how to solve this?

raumpolizei · February 25, 2020, 14:04

Hey there, your BCs seem to constrain the coupling of momentum and pressure equation. But to be sure, it would be good to know the set of equations that you are trying to solve. Here is a suggestion for your BCs.
At the inlet:
fixedValue for velocity, zeroGradient for pressure.
At the outlet the opposite:
zeroGradient for velocity, fixedValue for pressure (dynamic pressure p = 0).
Hope this helps. Good luck!

Saideep · February 26, 2020, 08:30

I am solving the Darcys single phase flow equation.

$U = -\frac{k}{\mu}\nabla p$

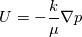So, there is no momentum involved here. I solve for pressure (p) initially and then compute the velocity (U).

I am aware of the fixed rate boundary conditions you specified but I cannot use them. I have varying flux based on fixed pressure gradient rather.

raumpolizei · February 26, 2020, 09:21

Hey,
if I understand the problem correctly, it seems that there are two possibilities to solve this equation: (1) prescribing a pressure gradient and solving for the velocity, (2) set the velocity and solve for the pressure. You are doing the latter. You said that you are solving for the pressure and then computing the velocity? What do you mean by that? Have you tried to supply a velocity field and see what pressure gradient is resulting from the darcy equation? To do this, it is crucial that you set the outlet to fixedValue 0. The pressure value obtained at the inlet will be depending on the velocity you prescribed. Hope this helps.

Similar Threads
Thread	Thread Starter	Forum	Replies	Last Post
Error - Solar absorber - Solar Thermal Radiation	MichaelK	CFX	12	September 1, 2016 06:15
Problem in setting Boundary Condition	Madhatter92	CFX	12	January 12, 2016 05:39
Is Playstation 3 cluster suitable for CFD work	hsieh	OpenFOAM	9	August 16, 2015 15:53
An error has occurred in cfx5solve:	volo87	CFX	5	June 14, 2013 18:44
Convective Heat Transfer - Heat Exchanger	Mark	CFX	6	November 15, 2004 16:55

February 25, 2020, 14:04		#2
raumpolizei Member Join Date: Dec 2018 Location: Darmstadt, Germany Posts: 87 Rep Power: 8	Hey there, your BCs seem to constrain the coupling of momentum and pressure equation. But to be sure, it would be good to know the set of equations that you are trying to solve. Here is a suggestion for your BCs. At the inlet: fixedValue for velocity, zeroGradient for pressure. At the outlet the opposite: zeroGradient for velocity, fixedValue for pressure (dynamic pressure p = 0). Hope this helps. Good luck!

February 26, 2020, 08:30		#3
Saideep Senior Member Saideep Join Date: Apr 2015 Location: INDIA Posts: 203 Rep Power: 12	I am solving the Darcys single phase flow equation. $U = -\frac{k}{\mu}\nabla p$ So, there is no momentum involved here. I solve for pressure (p) initially and then compute the velocity (U). I am aware of the fixed rate boundary conditions you specified but I cannot use them. I have varying flux based on fixed pressure gradient rather.

February 26, 2020, 09:21		#4
raumpolizei Member Join Date: Dec 2018 Location: Darmstadt, Germany Posts: 87 Rep Power: 8	Hey, if I understand the problem correctly, it seems that there are two possibilities to solve this equation: (1) prescribing a pressure gradient and solving for the velocity, (2) set the velocity and solve for the pressure. You are doing the latter. You said that you are solving for the pressure and then computing the velocity? What do you mean by that? Have you tried to supply a velocity field and see what pressure gradient is resulting from the darcy equation? To do this, it is crucial that you set the outlet to fixedValue 0. The pressure value obtained at the inlet will be depending on the velocity you prescribed. Hope this helps.