 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Jeferson Souza
Join Date: Jan 2012
Location: Brazil
Posts: 19
Rep Power: 14  |
I'm trying to understand which is the difference between setting up the thermoModel to hConst or eConst.
Reading the documentation and also this post (When choose sensibleInternalEnergy or sensibleEnthalpy in thermophysicalProperties), I have understood that this setup is used to define which form of the energy equation should be used: hConst for enthalpy and eConst for internal energy. The problem is that I'm getting different solution, with the same problem, for each of these models. I'm using chtMultRegionFoam in openFoam 8. Both solid and fluid regions are solved. Natural convection (Boussinesq) is used in fluid zones. I would be very thankful if someone could explain (or indicate a link to read) which is the difference between these two models. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Join Date: Apr 2020
Location: UK
Posts: 696
Rep Power: 14  |
Jeferson - that's curious. Is it a significant difference, or just a minor convergence difference?
It's worth checking that you have made the necessary changes to your input data and boundary conditions. For example, when you change from hConst to eConst, you need to change the specific heat that you define in thermophysicalProperties from Cp (constant pressure) to Cv = Cp/gamma (constant volume), etc. |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Jeferson Souza
Join Date: Jan 2012
Location: Brazil
Posts: 19
Rep Power: 14  |
Hy Tobermory, thanks for you answer.
Results are quite different. About 10 K (from 350K to 360K). I have notice that when I change from hConst (using Cp) to eConst (using Cv = Cp), results are identical. In other words, when gamma is equal to 1, both solutions converge to the same result. What would be the gamma? The ratio between Cp and Cv? It should be equal to 1 for an incomprehensible fluid, however I'm using air. I have used Cp = 1007 J/kg K with the hConst solution and Cv = 712 J/kg K with the eCont solution. With these values, i got the 10 K difference. |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Join Date: Sep 2013
Posts: 353
Rep Power: 20  |
The implementation in the code:
he is h or e and the ? : part is c++ for if he=e use the first equation otherwise the second. Code:
fvScalarMatrix EEqn
(
fvm::div(phi, he)
+ (
he.name() == "e"
? fvc::div(phi, volScalarField("Ekp", 0.5*magSqr(U) + p/rho))
: fvc::div(phi, volScalarField("K", 0.5*magSqr(U)))
)
- fvm::laplacian(turb.alphaEff(), he)
==
rho*(U&g)
+ rad.Sh(thermo)
+ fvOptions(rho, he)
);
Internal Energy: Enthalpy: with alphaEff for h  and for e 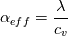 The underlying full equations are hence: Full Energy Equation: 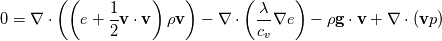 Full Energy equation formulated with Enthalpy: 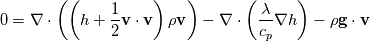 As you can see there is but one difference between these (keep in mind these equations are identical, just a different formulation). However the additional pressure work term in there is a difference from a numerical solution procedure. It is either an explicit source term when solving for e, or an implicit part of the enthalpy h. In most cases however you can split the equations above into a thermal part and the kinetic energy part. And here the thermal energy usually dominates in heat transfer, hence kinetic energy is negligible. Energy equation with removed kinetic energy: 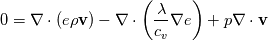 Enthalpy with removed kinetic energy: 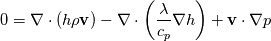 As quickly copied by other posts of mine. Which is preferable depends on last term in there. This is a source term, it does not include the variable we are solving for (h or e). And if this term acts as a source or sink is what determines it's numerical stability. The divergence of the velocity field is for example for incompressible flows 0. Hence the last term vanishes for the e solution. Which is why for incompressible stationary flows the e solution might be preferable. And for your problem: For incompressible fluids cp=cv Hence this might simply be how alpha is looked up due to you using rhoConst |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Jeferson Souza
Join Date: Jan 2012
Location: Brazil
Posts: 19
Rep Power: 14  |
What would be lambda? kappa/rho?
|
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Join Date: Apr 2020
Location: UK
Posts: 696
Rep Power: 14  |
Jeferson - yes - check out post #4 in the following thread, where you can see the derivation of the term:
question about fvm::laplacian(turbulence->alphaEff(), he) in rhoSimpleFoam |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Join Date: Sep 2013
Posts: 353
Rep Power: 20  |
no it's just kappa. I'm used to writing thermal conductivity as lambda.
|
|
|
|

|
|
|
|
|
#8 |
|
New Member
Jeferson Souza
Join Date: Jan 2012
Location: Brazil
Posts: 19
Rep Power: 14  |
I still "fighting" with this problem.
In the case that I'm using thermoType { ... thermo eConst; equationOfState Boussinesq; ... } I have to inform Cv instead of Cp. I have two doubts: 1) how is Cp calculated? 2) how is Pr (Prandtl) calculated? I took a look at the suggested threads, but I'm still confused. |
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
Join Date: Apr 2020
Location: UK
Posts: 696
Rep Power: 14  |
Ok - I think that I have found the answer. When using eConst thermo, you define the thermo using Cv, as you have stated. Line 137 of eConstThermoI.H shows an example of where Cp is used in the coding:
Code:
template<class EquationOfState>
inline Foam::scalar Foam::eConstThermo<EquationOfState>::S
(
const scalar p,
const scalar T
) const
{
return Cp(p, T)*log(T/Tstd) + EquationOfState::Sv(p, T);
}
Code:
inline scalar Cp
(
const scalar p,
const scalar T
) const
{
return Cv(p, T) + EquationOfState::CpMCv(p, T);
}
Code:
template<class Specie>
inline Foam::scalar Foam::Boussinesq<Specie>::CpMCv
(
scalar p,
scalar T
) const
{
return 0;
}
|
|
|
|

|
|
|
|
|
#10 |
|
New Member
Jeferson Souza
Join Date: Jan 2012
Location: Brazil
Posts: 19
Rep Power: 14  |
Thanks a lot
Now things make sense. This is kind of tricky and difficult to "guess". There was not doubt in openFoam 7, since the combination of eConst with Boussinesq was not possible, but when I tried to use openFoam 8 things got confusing. |
|
|
|

|
|
 |
| Tags |
| energy equation |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| equationOfState icoTabulated error | carl_r | OpenFOAM Running, Solving & CFD | 3 | March 14, 2022 06:05 |
| FOAM FATAL IO ERROR: Unknown rhoThermo type | rupak504 | OpenFOAM Running, Solving & CFD | 1 | November 22, 2021 01:40 |
| "Unknown psiThermo type" why not on the list?? | mexicalense | OpenFOAM Running, Solving & CFD | 3 | March 22, 2021 13:50 |
| WLF from OF7 | Pisolino85 | OpenFOAM | 2 | April 26, 2020 06:34 |
| compile of new combination of property in thermophisicalpropery | milad653279 | OpenFOAM Running, Solving & CFD | 4 | April 6, 2017 04:35 |