 |
|
|
[Sponsors] | |||||
Discretization of mass conservation equation in a 2D staggered grid |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
kiwi
Join Date: Apr 2016
Posts: 3
Rep Power: 10  |
Hi everybody,
As mentioned in the title I would like to solve the mass conservation to simulate the boiling phenomenon into a tube bundle. I am facing some issues to discretize these equations into a staggered grid after to have applied an integration into a finite volume. Accordingly to the classical staggered grid: the flow properties are content in the control volume whereas the velocity information is on the bondaries of this control volume. Here is a representation of the staggered grid I use (for the notations)  My governing equation is: 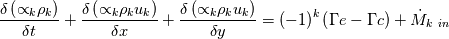 Where the subcript k is for the phase type (1 for liquid; 2 for gas)  and and 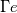 are the evaporation and condensation rate defined as: are the evaporation and condensation rate defined as: 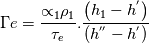 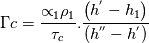 Where H" is the staturated enthalpy of the gas, H' is the saturated enthalpy of the liquid and  is the relaxation time. First question: does someone have a definition to calculate that relaxation time? is the relaxation time. First question: does someone have a definition to calculate that relaxation time?After having integrated the mass conservation equation for the control volume I;J, I get: ![\left[{\left({\propto }_1{\rho }_1\right)}^n_{I;J}-{\left({\propto }_1{\rho }_1\right)}^{n-1}_{I;J}\right]\frac{\mathrm{\Delta }\mathrm{x}\mathrm{\Delta }\mathrm{y}}{\mathrm{\Delta }\mathrm{t}}+\left[{\left({\propto }_1{\rho }_1u_1\right)}^n_{i+1;j}-{\left({\propto }_1{\rho }_1u_1\right)}^n_{i;j}\right] \left[{\left({\propto }_1{\rho }_1\right)}^n_{I;J}-{\left({\propto }_1{\rho }_1\right)}^{n-1}_{I;J}\right]\frac{\mathrm{\Delta }\mathrm{x}\mathrm{\Delta }\mathrm{y}}{\mathrm{\Delta }\mathrm{t}}+\left[{\left({\propto }_1{\rho }_1u_1\right)}^n_{i+1;j}-{\left({\propto }_1{\rho }_1u_1\right)}^n_{i;j}\right]](/Forums/vbLatex/img/8282bd4f7459b2078fc21636cc04a532-1.gif) ![\mathrm{\Delta }\mathrm{y}+\left[{\left({\propto }_1{\rho }_1v_1\right)}^n_{i;j+1}-{\left({\propto }_1{\rho }_1v_1\right)}^n_{i;j}\right]\mathrm{\Delta }\mathrm{x}= \mathrm{\Delta }\mathrm{y}+\left[{\left({\propto }_1{\rho }_1v_1\right)}^n_{i;j+1}-{\left({\propto }_1{\rho }_1v_1\right)}^n_{i;j}\right]\mathrm{\Delta }\mathrm{x}=](/Forums/vbLatex/img/7e6bf4a90c4b5cf941a10093ea3da21b-1.gif) ![\ {\left[\mathrm{-}\mathrm{\Gamma }e+\mathrm{\Gamma }c+{\dot{M}}_{1\ in}\right]}^n_{I;J}\mathrm{\Delta }\mathrm{x}\mathrm{\Delta }\mathrm{y} \ {\left[\mathrm{-}\mathrm{\Gamma }e+\mathrm{\Gamma }c+{\dot{M}}_{1\ in}\right]}^n_{I;J}\mathrm{\Delta }\mathrm{x}\mathrm{\Delta }\mathrm{y}](/Forums/vbLatex/img/53666919e69f980fbd944ad461e04169-1.gif) By making the assumption that the velocity field is known, I can resolve this equation and find the void fraction and the density. My issue arrives now: I don't know how to approximate the terms of void fraction and density which are at the bondaries of the control volume because the information is not stocked there (ex: 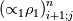 ) )If someone can help me on this I will be very grateful. In advance, thank you. Kiwi |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
your grid arrangement is not totally clear to me from the picture...
I immagine that rho(i,j), u(i,j), v(i,j) are staggered each other, right? For example, if rho(i,j) is at the position x(i),y(j), then u(i,j) is at x(i)+dx/2,y(j) and v(i,j) is at x(i),y(j)+dy/2? If it is true, the integration for rho is for the CV centred at x(i),y(j). |
|
|
|

|
|
|
|
|
#3 |
|
New Member
kiwi
Join Date: Apr 2016
Posts: 3
Rep Power: 10  |
Hi FMdenaro and thank you for your answer.
Yes you are right; if we use the notation (i,j) (i+1/2) and (j+1/2) the equation can consequenlty be written as: ![\left[{\left({\propto }_1{\rho }_1\right)}^n_{i;j}-{\left({\propto }_1{\rho }_1\right)}^{n-1}_{i;j}\right]\frac{\mathrm{\Delta }\mathrm{x}\mathrm{\Delta }\mathrm{y}}{\mathrm{\Delta }\mathrm{t}}+\left[{\left({\propto }_1{\rho }_1u_1\right)}^n_{i+1/2;j}-{\left({\propto }_1{\rho }_1u_1\right)}^n_{i-1/2;j}\right] \left[{\left({\propto }_1{\rho }_1\right)}^n_{i;j}-{\left({\propto }_1{\rho }_1\right)}^{n-1}_{i;j}\right]\frac{\mathrm{\Delta }\mathrm{x}\mathrm{\Delta }\mathrm{y}}{\mathrm{\Delta }\mathrm{t}}+\left[{\left({\propto }_1{\rho }_1u_1\right)}^n_{i+1/2;j}-{\left({\propto }_1{\rho }_1u_1\right)}^n_{i-1/2;j}\right]](/Forums/vbLatex/img/9571f7450ff66ae81b93babb25cc6da8-1.gif) ![\mathrm{\Delta }\mathrm{y}+\left[{\left({\propto }_1{\rho }_1v_1\right)}^n_{i;j+1/2}-{\left({\propto }_1{\rho }_1v_1\right)}^n_{i;j-1/2}\right]\mathrm{\Delta }\mathrm{x}= \mathrm{\Delta }\mathrm{y}+\left[{\left({\propto }_1{\rho }_1v_1\right)}^n_{i;j+1/2}-{\left({\propto }_1{\rho }_1v_1\right)}^n_{i;j-1/2}\right]\mathrm{\Delta }\mathrm{x}=](/Forums/vbLatex/img/63b75d7c3795c47ea63eb679b0d1caf4-1.gif) ![\ {\left[\mathrm{-}\mathrm{\Gamma }e+\mathrm{\Gamma }c+{\dot{M}}_{1\ in}\right]}^n_{i;j}\mathrm{\Delta }\mathrm{x}\mathrm{\Delta }\mathrm{y} \ {\left[\mathrm{-}\mathrm{\Gamma }e+\mathrm{\Gamma }c+{\dot{M}}_{1\ in}\right]}^n_{i;j}\mathrm{\Delta }\mathrm{x}\mathrm{\Delta }\mathrm{y}](/Forums/vbLatex/img/9dfaf2891508bba7b9be12295b39e6a3-1.gif) Is it more clear for you with that writing? So you mean that for the terms 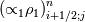 I can make the approximation I can make the approximation 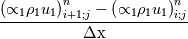 ? ?So the equation would become: ![\left[{\left({\propto }_1{\rho }_1\right)}^n_{i;j}-{\left({\propto }_1{\rho }_1\right)}^{n-1}_{i;j}\right]\frac{\mathrm{\Delta }\mathrm{x}\mathrm{\Delta }\mathrm{y}}{\mathrm{\Delta }\mathrm{t}}+ \left[{\left({\propto }_1{\rho }_1\right)}^n_{i;j}-{\left({\propto }_1{\rho }_1\right)}^{n-1}_{i;j}\right]\frac{\mathrm{\Delta }\mathrm{x}\mathrm{\Delta }\mathrm{y}}{\mathrm{\Delta }\mathrm{t}}+](/Forums/vbLatex/img/6f1878790ee2f46f5c1ce47f4e2eb0f4-1.gif) ![\left[{\frac{{\left({\propto }_1{\rho }_1\right)}^n_{i+1;j}-{\left({\propto }_1{\rho }_1\right)}^n_{i;j}}{\mathrm{\Delta }\mathrm{x}}\left(u_1\right)}^n_{i+{1}/{2};j}-{\frac{{\left({\propto }_1{\rho }_1\right)}^n_{i;j}-{\left({\propto }_1{\rho }_1\right)}^n_{i-1;j}}{\mathrm{\Delta }\mathrm{x}}\left(u_1\right)}^n_{i-{1}/{2};j}\right]\mathrm{\Delta }\mathrm{y}+ \left[{\frac{{\left({\propto }_1{\rho }_1\right)}^n_{i+1;j}-{\left({\propto }_1{\rho }_1\right)}^n_{i;j}}{\mathrm{\Delta }\mathrm{x}}\left(u_1\right)}^n_{i+{1}/{2};j}-{\frac{{\left({\propto }_1{\rho }_1\right)}^n_{i;j}-{\left({\propto }_1{\rho }_1\right)}^n_{i-1;j}}{\mathrm{\Delta }\mathrm{x}}\left(u_1\right)}^n_{i-{1}/{2};j}\right]\mathrm{\Delta }\mathrm{y}+](/Forums/vbLatex/img/16cfa873c68bd04cae4b14db59a502e3-1.gif) ![\left[{\frac{{\left({\propto }_1{\rho }_1\right)}^n_{i;j+1}-{\left({\propto }_1{\rho }_1\right)}^n_{i;j}}{\mathrm{\Delta }\mathrm{y}}\left(v_1\right)}^n_{i;j+{1}/{2}}-{\frac{{\left({\propto }_1{\rho }_1\right)}^n_{i;j}-{\left({\propto }_1{\rho }_1\right)}^n_{i;j-1}}{\mathrm{\Delta }\mathrm{y}}\left(v_1\right)}^n_{i;j-{1}/{2}}\right]\mathrm{\Delta }\mathrm{x}= \left[{\frac{{\left({\propto }_1{\rho }_1\right)}^n_{i;j+1}-{\left({\propto }_1{\rho }_1\right)}^n_{i;j}}{\mathrm{\Delta }\mathrm{y}}\left(v_1\right)}^n_{i;j+{1}/{2}}-{\frac{{\left({\propto }_1{\rho }_1\right)}^n_{i;j}-{\left({\propto }_1{\rho }_1\right)}^n_{i;j-1}}{\mathrm{\Delta }\mathrm{y}}\left(v_1\right)}^n_{i;j-{1}/{2}}\right]\mathrm{\Delta }\mathrm{x}=](/Forums/vbLatex/img/21199a9803edceaeef0febd14b175019-1.gif) ![\ {\left[\mathrm{-}\mathrm{\Gamma }e+\mathrm{\Gamma }c+{\dot{M}}_{1\ in}\right]}^n_{i;j}\mathrm{\Delta }\mathrm{x}\mathrm{\Delta }\mathrm{y} \ {\left[\mathrm{-}\mathrm{\Gamma }e+\mathrm{\Gamma }c+{\dot{M}}_{1\ in}\right]}^n_{i;j}\mathrm{\Delta }\mathrm{x}\mathrm{\Delta }\mathrm{y}](/Forums/vbLatex/img/9dfaf2891508bba7b9be12295b39e6a3-1.gif) Is that correct ? I read also that we can do this approximation with the UPWIND scheme but I am not confident to use this scheme because it is based on the value of the velocity; for example: 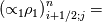 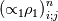 if if 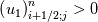 OR 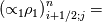 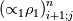 if if 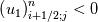 But I have also make the test for 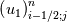 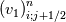 and and 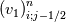 so the fill in of my matrix coefficients become very tough ... so the fill in of my matrix coefficients become very tough ...What is the best option? |
|
|
|

|
|
|
|
|
#4 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
not at all ... you have a convective flux at one section it can not be discretized as first derivative! You can use zeroth-order polynomial in a first order upwind reconstruction or a linear polynomial for a second order reconstruction |
||
|
|

|
||
|
|
|
#5 |
|
New Member
kiwi
Join Date: Apr 2016
Posts: 3
Rep Power: 10  |
Understood I can't use a first derivative solution.
But I am not sure to fully understand what you mean by "linear polynomial for a second order reconstruction". Could you give me an example ? Thank you. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Setting the height of the stream in the free channel | kevinmccartin | CFX | 12 | October 13, 2022 21:43 |
| Las term in 2D axisymmetric mass conservation equation | logme | FLUENT | 0 | June 10, 2015 06:06 |
| error message | cuteapathy | CFX | 14 | March 20, 2012 06:45 |
| Question on the discretization of momentum equation in icoFoam | MPJ | OpenFOAM | 3 | October 4, 2011 09:44 |
| Question regarding non-uniform FVM staggered grid | quarkz | Main CFD Forum | 2 | June 18, 2011 17:18 |