 |
|
|
[Sponsors] | |||||
non dimensionalisation eddy viscosity, mixing length and turbulent shear stress |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Join Date: Jan 2019
Posts: 7
Rep Power: 7  |
||
|
|

|
|
|
|
|
#2 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,674
Rep Power: 66    |
You can non-dimensionalize anything anyway you want. The question is what you are going to do with these quantities later? Then you want to choose a non-dimensionalization that makes sense.
For example, the friction velocity isn't just a random non-dimensionalization of shear stress, but it is used because that's the characteristic velocity in the perturbatino when you do asymptotic analysis (i.e. u+ = y+ which happens only you scale u and y using u*). |
|
|
|

|
|
|
|
|
#3 | |
|
New Member
Join Date: Jan 2019
Posts: 7
Rep Power: 7  |
Quote:
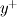 . Then I want to relate each of these properties to . Then I want to relate each of these properties to 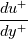 after which these will be evaluated in the limit after which these will be evaluated in the limit 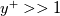 . Eventually I want to prove that in the overlap region the turbulent properties are independent of viscosity. . Eventually I want to prove that in the overlap region the turbulent properties are independent of viscosity.
|
||
|
|

|
||
|
|
|
#4 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,768
Rep Power: 71    |
Quote:
Actually, the eddy viscosity function is naturally non-dimensional when is computed from a non-dimensional expression. Just use the correct velocity and pressure reference quantities to work directly in terms of u+ and Re_tau. You can find in Sec.5 of this paper how to select the variables https://www.researchgate.net/publica...ection_methods |
||
|
|

|
||
|
|
|
#5 |
|
Senior Member
|
||
|
|

|
|
 |
| Tags |
| eddy viscosity, turbulence, viscous flow |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Use of k-epsilon and k-omega Models | Jade M | Main CFD Forum | 40 | January 27, 2023 07:18 |
| Turbulent Boundary condition, viscosity ratio and length scale | Bollonga | FLUENT | 80 | February 16, 2013 12:06 |
| setting value of turbulent intensity and turbulent viscosity ratio in wind tunnel | nuimlabib | Main CFD Forum | 0 | August 4, 2009 00:05 |
| Problem of Turbulent Viscosity Ratio Limited | David Yang | FLUENT | 3 | June 3, 2002 06:13 |
| Prandtl Mixing length Vs. Isotropic turbulent | Mohammad Kermani | Main CFD Forum | 0 | March 23, 2000 23:06 |