 |
|
|
[Sponsors] | |||||
Partial Derivative Using Fourier Transform (FFTW) in 2D |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Negar
Join Date: May 2022
Posts: 2
Rep Power: 0  |
Hello!
I am trying to calculate the partial derivative of the function Sin(x)Sin(y) along the x-direction using Fourier Transform (FFTW library in C++). I take my function from real to Fourier space (fftw_plan_dft_r2c_2d), multiply the result by -i * kappa array (wavenumber/spatial frequency), and then transform the result back into real space (fftw_plan_dft_c2r_2d). Finally, I divide the result by the size of my 2D array Nx*Ny (I need to do this based on the documentation). However, the resulting function is scaled up by some value and the amplitude is not 1. Code:
#define Nx 360
#define Ny 360
#define REAL 0
#define IMAG 1
#define Pi 3.14
#include <stdio.h>
#include <math.h>
#include <fftw3.h>
#include <iostream>
#include <iostream>
#include <fstream>
#include <iomanip>
int main() {
int i, j;
int Nyh = Ny / 2 + 1;
double k1;
double k2;
double *signal;
double *result2;
double *kappa1;
double *kappa2;
double df;
fftw_complex *result1;
fftw_complex *dfhat;
signal = (double*)fftw_malloc(sizeof(double) * Nx * Ny );
result2 = (double*)fftw_malloc(sizeof(double) * Nx * Ny );
kappa1 = (double*)fftw_malloc(sizeof(double) * Nx * Nyh );
result1 = (fftw_complex*)fftw_malloc(sizeof(fftw_complex) * Nx * Nyh);
dfhat = (fftw_complex*)fftw_malloc(sizeof(fftw_complex) * Nx * Nyh);
for (int i = 0; i < Nx; i++){
if ( i < Nx/2 + 1)
k1 = 2 * Pi * (-Nx + i) / Nx;
else
k1 = 2 * Pi * i / Nx;
for (int j = 0; j < Nyh; j++){
kappa1[j + Nyh * i] = k1;
}
}
fftw_plan plan1 = fftw_plan_dft_r2c_2d(Nx,Ny,signal,result1,FFTW_ESTIMATE);
fftw_plan plan2 = fftw_plan_dft_c2r_2d(Nx,Ny,dfhat,result2,FFTW_ESTIMATE);
for (int i=0; i < Nx; i++){
for (int j=0; j < Ny; j++){
double x = (double)i / 180 * (double) Pi;
double y = (double)j / 180 * (double) Pi;
signal[j + Ny * i] = sin(x) * sin(y);
}
}
fftw_execute(plan1);
for (int i = 0; i < Nx; i++) {
for (int j = 0; j < Nyh; j++) {
dfhat[j + Nyh * i][REAL] = 0;
dfhat[j + Nyh * i][IMAG] = 0;
dfhat[j + Nyh * i][IMAG] = -result1[j + Nyh * i][REAL] * kappa1[j + Nyh * i];
dfhat[j + Nyh * i][REAL] = result1[j + Nyh * i][IMAG] * kappa1[j + Nyh * i];
}
}
fftw_execute(plan2);
for (int i = 0; i < Nx; i++) {
for (int j = 0; j < Ny; j++) {
result2[j + Ny * i] /= (Nx*Ny);
}
}
for (int j = 0; j < Ny; j++) {
for (int i = 0; i < Nx; i++) {
std::cout <<std::setw(15)<< result2[j + Ny * i];
}
std::cout << std::endl;
}
fftw_destroy_plan(plan1);
fftw_destroy_plan(plan2);
fftw_free(result1);
fftw_free(dfhat);
return 0;
}
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
I don't think someone will debug your code for you. However, some suggestions.
Matlab code for even 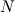 in 1D (MATLAB uses FFTW): in 1D (MATLAB uses FFTW):Code:
N=64; L=2*pi; dx=L/N; x=linspace(0,L-dx,N); f=sin(x); k(1:N/2)=1i*(0:N/2-1); k(N/2+2:N)=1i*(-N/2+1:-1); % Consider the Nyquist mode my young Padawan k(N/2+1)=0; fhat=fft(f); fhatx=k.*fhat; fx=ifft(fhatx);
Note that here 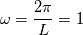 . Otherwise you have to scale the . Otherwise you have to scale the 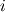 -th mode with -th mode with 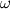 . The mode vector has to be handled different for odd . The mode vector has to be handled different for odd 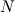 . Morever, the two dimensional derivative can be derived analog to the one dimensional derivative since the discrete Fourier transform FFT2 is a tensor product operation which can be derived by applying the FFT1 . Morever, the two dimensional derivative can be derived analog to the one dimensional derivative since the discrete Fourier transform FFT2 is a tensor product operation which can be derived by applying the FFT1 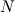 -times linewise. -times linewise.Summarizing: 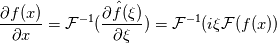 . .Regards |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Poly T
Join Date: May 2022
Posts: 24
Rep Power: 3  |
The "wrong" scaling factor should already tell you what the issue is. Also, as suggested by others here: Start with 1D FFT, understand what is going on there, then do 2D via tensor extension.
|
|
|
|

|
|
 |
| Tags |
| c++, derivative, fftw3 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| linear vs quadratic triangle and divergence theorem | naffrancois | Main CFD Forum | 19 | September 30, 2021 09:29 |
| Finite Volume Simple Code Problem | DAVIDRASC | Main CFD Forum | 13 | September 20, 2020 14:21 |
| Partial derivative of VolvectorField with respect to Temperature | SHUBHAM9595 | OpenFOAM Programming & Development | 0 | August 4, 2020 14:59 |
| Grid transformation to computational space | mech_eng_gr | Main CFD Forum | 1 | May 31, 2020 21:17 |
| Low Reynolds K Epsilon Launder Sharma Model Functions Doubt... | Ruonin | Main CFD Forum | 17 | February 17, 2014 09:52 |