 |
|
|
[Sponsors] | |||||
|
|
|
#21 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,769
Rep Power: 71    |
Quote:
No, FVM is not like FDM, it is multidimensional not factorized as you wrote. That would be a very rude approximation as you disregards the role of the surface integration of the flux. |
||
|
|

|
||
|
|
|
#22 |
|
Senior Member
Join Date: Mar 2009
Posts: 151
Rep Power: 17  |
Quote:
OK, this is in many text-books. This also explains how we can cancel out opposing faces etc. I do not see how this produces an isotropic diffusivity coefficient though. This should produce a numerical diffusion for the triangle example, right? On the diagonal side we should have both x-, and y-dependence on the error, but on the orthogonal side of the triangle it is just an x-dependence (right triangle as basis). Although the error is directional, it will cancel out in the next triangle, when the triangle is reversed. Seems like a variation of my argument only that it is based on FDM theory.
__________________
"Trying is the first step to failure." - Homer Simpson |
|
|
|

|
|
|
|
|
#23 | |
|
Senior Member
Join Date: Mar 2009
Posts: 151
Rep Power: 17  |
Quote:
Why would I disregard the surface integration? Not sure what I wrote that made you draw that conclusion. 
__________________
"Trying is the first step to failure." - Homer Simpson |
||
|
|

|
||
|
|
|
#24 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,769
Rep Power: 71    |
Quote:
Thus, the computational molecule appears more isotropic for any direction of the flow. Use the QUICK as an example. |
||
|
|

|
||
|
|
|
#25 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,675
Rep Power: 66    |
Replace x with the displacement vector r and interpret u not as the x-velocity but as the full velocity vector and it is an isotropic diffusion term. Literally just make them 2D or 3D vectors or do it using components and do the FVM summation and it turns into 2D/3D Laplacian. In other words, work out the taylor series for the multidimensional face flux.
We are talking about error cancellation on faces of the same triangle, not error cancellation when going from one triangle to the next, that itself is a type of error.  is not a rook or bishop problem and no privileged direction. The flow aligning with the face normals is a different issue on top of numerical diffusion. is not a rook or bishop problem and no privileged direction. The flow aligning with the face normals is a different issue on top of numerical diffusion.
|
|
|
|

|
|
|
|
|
#26 | ||
|
Senior Member
Join Date: Mar 2009
Posts: 151
Rep Power: 17  |
Quote:
OK, so according to your definition, will we have numerical diffusion for the triangle example? Quote:
OK, then I understand the confusion in this thread. I must have misunderstood the concept of numerical diffusion. To my defense, almost all examples show an oblique flow and smearing of an interface, such as figure 1 or the classical 45 degree flow across a quad-structured domain. So when we talk about "preferred directions" in the context of numerical diffusion, what does the authors mean in this case if it is not about face normals? And finally, what should I call the diffusion-like effect that appears when the flow is not aligned with the face normals? Is it dispersion?
__________________
"Trying is the first step to failure." - Homer Simpson |
|||
|
|

|
|||
|
|
|
#27 | |
|
Senior Member
|
Quote:
Let's stay with the steady, linear scalar convection equation, then we simply have to solve: 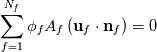 where the f subscript indicates faces and 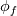 is meant to be the exact face average, so that the integration and, in fact, the whole equation is still exact (assuming a constant velocity field and planar volume faces). is meant to be the exact face average, so that the integration and, in fact, the whole equation is still exact (assuming a constant velocity field and planar volume faces).Now, accoring to the mean value theorem, there is a point on each face where one can evaluate 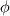 and get the exact face average value and get the exact face average value 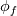 . So, without further approximation let us assume that we know such point for each face and decide to evaluate our function just there. . So, without further approximation let us assume that we know such point for each face and decide to evaluate our function just there.I hope that it is clear how, up to now, no matter what cell shapes we have, there is no error at all in our equations. Unfortunately, we now have to introduce some. First, let us assume that we are using a cell centered FV approach (which is what most people are familiar with, but makes little difference in this example). What this practically means is that we know 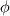 in cell centers but we need it in face centers (superseding on the fact that what we know in cell centers is probably different from what we need in face centers, as this becomes supercumbersome without a time derivative). We are going to use interpolation for it, and this is the only error we have in our approach up to this point. Again, this is independent from the cell shape. There is interpolation and, because of that, there is error. in cell centers but we need it in face centers (superseding on the fact that what we know in cell centers is probably different from what we need in face centers, as this becomes supercumbersome without a time derivative). We are going to use interpolation for it, and this is the only error we have in our approach up to this point. Again, this is independent from the cell shape. There is interpolation and, because of that, there is error.Now, and this is the first point to highlight with respect to the discussion so far, we can't say more about the nature of the error until we decide what sort of interpolation we are going to use. That is, which convective scheme. The second thing to notice is how, no matter what error we do, faces parallel to the velocity vector do not conribute any error. That is, they do not contribute any OF THE SAME ERROR that non aligned faces instead contribute to. Error contribution becomes potentially maximal for fully perpendicular faces (e.g., in 1D). Potentially because it depends from the scheme and the actual derivatives in the solution. Let's clarify this by considering a general first order scheme (not necessarily upwind): 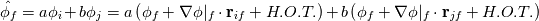 where 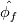 is our approximation for is our approximation for 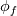 and and 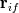 and and 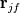 are the vectors connecting the face point f with the neighbor cell centers i and j. a and b are unspecified coefficients which must obey a+b=1. are the vectors connecting the face point f with the neighbor cell centers i and j. a and b are unspecified coefficients which must obey a+b=1.This tells us that, in our case, independently from the nature of the scheme, a first order scheme will have a first order error on a face only if the face is not parallel to the velocity AND the solution in the face point has a gradient along the two directions 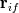 and and 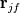 (depending from which one is actually used in the scheme). This should be obvious, as we make no error if the function is constant as long as (a+b)=1. I hope that it is clear that the latter error has nothing to do with flow alignment per se. (depending from which one is actually used in the scheme). This should be obvious, as we make no error if the function is constant as long as (a+b)=1. I hope that it is clear that the latter error has nothing to do with flow alignment per se.Going forward, we speak about a first order diffusion error when the first order approximation above is used (note how the gradient term error is indeed in the form of a diffusion term) AND the combined effect of the coefficients a and b and the grid (trough the r vectors) is such that it leads to a positive diffusion coefficient. For a uniform regular grid, you can expect this to be the case whenever the upwind cell gets a higher coefficents than the downwind one, but this is only a special case. For general cases you can only be sure if the upwind cell gets the full weight. Note how first order diffusion can be completely eliminated if, for a given face, we can pick up and b such that 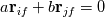 . Again, this has nothing to do with the face alignment with respect to the solution. . Again, this has nothing to do with the face alignment with respect to the solution.Finally, arguments similar to the latter can be invoked in order to show that error terms on opposite faces of a cell will cancel each other under the proper conditions of regularity and scheme selection. Hopefully all of this clarifies the matter. Obviously, when you add non exact surface integration the matter becomes more contrived, but the reasoning remains valid. Last edited by sbaffini; November 29, 2022 at 11:18. Reason: Edited for clarity |
||
|
|

|
||
|
|
|
#28 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,769
Rep Power: 71    |
Quote:
You can understand the topic by starting from the FTUS in 2D with u=v= constant>0 on a structured cartesian grid. From such scheme, evaluate then the modified equation and have a look to the first order terms that appear. You should discover three terms acting as additional physical-like effects. Try to repeat the same for a different scheme, for example the FTCS (that you know is unconditionally unstable) or the Lax-Wendroff (that is conditionally stable). Each scheme will give you different answers to the topic of the numerical diffusion. |
||
|
|

|
||
|
|
|
#29 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,769
Rep Power: 71    |
Quote:
Paolo, just an observation, if you want to use the first order upwind the value at a face is not linearly interpolated but it is piecewise constant from left or right (depending on the sign). Using a linear interpolation makes the scheme second order (the accuracy order in a FVM is dictated by the truncation error of the flux reconstruction, not by the derivatives as happens in FDM). But your arguments are clear. I would be glad to know if some published paper has never formalized the topic for general grids. |
|
|
|

|
|
|
|
|
#30 | |
|
Senior Member
|
Quote:
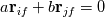 . .As far as I can remember, there are several papers or theses that treat this, also in relation to polys and other shapes. Still, I can't remember any of them now. EDIT: I have now removed from the post above the part where I first mentioned the upwind, which was indeed unnecessary and promoted confusion. Last edited by sbaffini; November 29, 2022 at 11:16. Reason: Added a comment |
||
|
|

|
||
|
|
|
#31 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,769
Rep Power: 71    |
Quote:
I don't remember any specific paper when an expression of the modified equation is detailed for a FVM on triangular grids...I mean an expression where the local truncation error is expressed in terms of surface integral of higher order fluxes. |
|
|
|

|
|
|
|
|
#32 | |
|
Senior Member
|
Quote:
The other line is the one by Hiro Nishikawa. Altough he never gets into the details of specific cell geometries, I remember that some of his recent works deal exactly with the modified differential equation for FV equations on unstructured grids. |
||
|
|

|
||
|
|
|
#33 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,769
Rep Power: 71    |
Quote:
At the best of my knowledge, both addressed simple cases, Nishikawa illustratated some work on the modified equation (the local truncation error is in differential form) but that is somehow different from what I mean. A relevant part comes from the time integration of the cell-averaged values. |
||
|
|

|
||
|
|
|
#34 | ||||
|
Senior Member
Join Date: Mar 2009
Posts: 151
Rep Power: 17  |
Thank you for a very nice explanation Sbaffini! Could you also just give your opinion if your explanation also explains the triangle example I provided?
Quote:
Quote:
Quote:
Quote:
Quote:
Quote:
So with proper regularity and scheme selection, it is correct to talk about "preferred directions" in the context of numerical diffusion when we compare tet vs hex vs poly?
__________________
"Trying is the first step to failure." - Homer Simpson |
|||||
|
|

|
|||||
|
|
|
#35 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,769
Rep Power: 71    |
Originally Posted by Ford Prefect
 I do not think the flow needs to be aligned with a coordinate direction, rather that the flow is orthogonal to the cell face normals where we do not wish to have information propagation what do you mean? Clearly in this case the convective flux is exactly zero ... you have to consider cases wherein the flow is not orthogonal to the normal unit vector to the face. |
|
|
|

|
|
|
|
|
#36 |
|
Senior Member
Join Date: Mar 2009
Posts: 151
Rep Power: 17  |
Quote:
__________________
"Trying is the first step to failure." - Homer Simpson |
|
|
|

|
|
|
|
|
#37 | |
|
Senior Member
|
Quote:
1) While this is a classical example and most conclusions are independent of this, let's always bear in mind that the original discontinuity in the scalar that we see in the pictures is such that most of the arguments I used are not valid. Yet, let just pretend it is a very high gradient, which might be a reasonable assumption for a fixed grid case 2) The original couple of images from ansys shows that there is no error for the hexa as the faces where the gradient is are all parallel to the flow and the grid is uniform in the scalar gradient direction. The tetra grid, instead, has most faces in the gradient zone that are not aligned with the flow. That's the main source of the difference and error for the tetra grid. This error is apparently diffusive in nature but, again, this is not related to flow alignment. 3) Your third picture is different from the ansys tetra one, because your high gradient part is in a zone where, despite the triangles, is completely aligned with the flow (it is indeed a splitted quad grid, with the splits happening in totally uniform zones). This, if it was ever needed, just confirms that cell shapes are not, per se, indications of anything 4) A polyhedral cell would behave exactly the same here if it could have the gradient part covered by flow aligned faces. But it can't at 100%. Which means that the poly grid would have more error than a properly tailored tri grid, contradicting any universal statement on poly vs tri My opinion is that any general statements on grids are bullshit because, as others have shown well before me, the grid purpose is to serve the numerical solution of a given problem with a given method and its quality is not independent from the solution and the method (except for some geometrical quantities that arise independently from them) |
||
|
|

|
||
|
|
|
#38 |
|
Senior Member
|
Another counter example would be a linear scalar distribution (in a plane normal to the constant velocity field, for simplicity) and a second order upwind scheme using, say, a lsq gradient. I would expect no error here for whatever grid and alignment.
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [ANSYS Meshing] Unexpected Transformation of Hex to Tet mesh. | Rajkool | ANSYS Meshing & Geometry | 0 | February 17, 2020 10:13 |
| [snappyHexMesh] No layers in a small gap | bobburnquist | OpenFOAM Meshing & Mesh Conversion | 6 | August 26, 2015 09:38 |
| [blockMesh] apparently the mesh doesn't want to be created in one direction | Maxime Thomas | OpenFOAM Meshing & Mesh Conversion | 1 | August 18, 2012 06:05 |
| [blockMesh] BlockMesh number internal faces and boundary | ynos | OpenFOAM Meshing & Mesh Conversion | 6 | December 13, 2011 05:36 |
| hex mesh vs. tet mesh (for FEM solvers) | Sam | Main CFD Forum | 0 | July 1, 2005 15:11 |