[Ford Prefect]

Hi,

In many references from proponents of polyhedral meshing it is often said that polyhedral cells have 6 preferred directions (for a 12 face polyhedral cell). A hexahedral cell has 3 and a tetrahedral cell has zero. This is then used as an argument for numerical diffusion (or minimisation of). I do not understand how this works. It seems to me that while a polyhedral cell may have 6 preferred directions it will then also have 6 directions that may be oblique to the flow, which of course will cause numerical diffusion.

As I understand it, the only way of avoiding numerical diffusion is across cell faces that are normal to the velocity vector. Triangles can be used for this, just as well as quads, but most text-book examples use an unstructured triangular mesh as comparison compared to a structured quad mesh and therefore it seems that triangles cannot be used.

As a comparison, figure 1 is from ANSYS best practice guidelines, and figure 2 is just a structured triangular mesh with the same type of comparison (cell values plotted, not node values).

Information propagates in small wiggles for the triangles as the cell centers are not aligned perfectly as for the quads, but that does not matter since the information transport is contained in the same quad that was split to create the triangles.

Anyways, for the general case with a fully unstructured mesh it may be easier to have parts of the domain aligned with a certain flow direction if quad/hex mesh is being used, so perhaps the text-book examples are OK.

However, I still do not understand the argument about "preferred directions" when it comes to polyhedral cells. The best argument for polyhedral cells is that we have more neighbours when calculating gradients, but that has no connection to the numerical diffusion.

What do you think, do you have any better explanation for the argument of polyhedral cells' preferred direction?

[FMDenaro]

"preferred direction" is somehow associated to structured grids and flow aligned with some coordinate direction.


However, I would consider the term "numerical diffusion" depending on the type of scheme, not the type of grid. A flow aligned along a structured grid direction can reduce the numerical diffusion of upwind but you can have also multidimensional FV reconstruction on unstructured grids with low numerical diffusion.

[arjun]

The main thing with polyhedrals is that the gradients calculated are more accurate and have much lesser control volume shape dependency. Any good numerical scheme in unstructured meshes depends on accuracy of these gradients.

This is why it is not straightforward to compared hex and polys. There will be cases where polys outperform hexes.

Originally Posted by Ford Prefect

Hi,

In many references from proponents of polyhedral meshing it is often said that polyhedral cells have 6 preferred directions (for a 12 face polyhedral cell). A hexahedral cell has 3 and a tetrahedral cell has zero. This is then used as an argument for numerical diffusion (or minimisation of). I do not understand how this works. It seems to me that while a polyhedral cell may have 6 preferred directions it will then also have 6 directions that may be oblique to the flow, which of course will cause numerical diffusion.

As I understand it, the only way of avoiding numerical diffusion is across cell faces that are normal to the velocity vector. Triangles can be used for this, just as well as quads, but most text-book examples use an unstructured triangular mesh as comparison compared to a structured quad mesh and therefore it seems that triangles cannot be used.

As a comparison, figure 1 is from ANSYS best practice guidelines, and figure 2 is just a structured triangular mesh with the same type of comparison (cell values plotted, not node values).

Information propagates in small wiggles for the triangles as the cell centers are not aligned perfectly as for the quads, but that does not matter since the information transport is contained in the same quad that was split to create the triangles.

Anyways, for the general case with a fully unstructured mesh it may be easier to have parts of the domain aligned with a certain flow direction if quad/hex mesh is being used, so perhaps the text-book examples are OK.

However, I still do not understand the argument about "preferred directions" when it comes to polyhedral cells. The best argument for polyhedral cells is that we have more neighbours when calculating gradients, but that has no connection to the numerical diffusion.

What do you think, do you have any better explanation for the argument of polyhedral cells' preferred direction?

[Ford Prefect]

Originally Posted by FMDenaro

"preferred direction" is somehow associated to structured grids and flow aligned with some coordinate direction.

I do not think the flow needs to be aligned with a coordinate direction, rather that the flow is orthogonal to the cell face normals where we do not wish to have information propagation (and that the cells are ordered in a structured manner so that as many cells as possible have the before mentioned "property"). It is evident from my example that even triangles can be aligned with the flow to have zero numerical diffusion, so perhaps the definition of "aligned with the flow" is a bit muddy.

It is interesting that you mention structured grids as an important aspect of numerical diffusion as opposed to cell types. As far as I can tell, there is a lot of discussion regarding cell types floating around (as is evident by the ANSYS slide i attached previously). They do the "hex vs tet" comparison, while it really should be a "structured vs unstructured" comparison.

Originally Posted by arjun

The main thing with polyhedrals is that the gradients calculated are more accurate and have much lesser control volume shape dependency. Any good numerical scheme in unstructured meshes depends on accuracy of these gradients.

This is why it is not straightforward to compared hex and polys. There will be cases where polys outperform hexes.

I agree. But how does this connect to numerical diffusion? With a standard UD scheme we would not need any gradient calculation so that should not affect numerical diffusion?

Perhaps you mean that the numerical diffusion question is a non-question (to which I would probably agree) regarding poly vs hex vs tet? I just wonder why many sources list "preferred directions" as something positive when comparing these three cell types.

[arjun]

Originally Posted by Ford Prefect

I agree. But how does this connect to numerical diffusion? With a standard UD scheme we would not need any gradient calculation so that should not affect numerical diffusion?

It is highly connected to numerical diffusion that is associated with advection term that you are considering here. There are many ways it can show up one of them would be to kick in the gradients limiters when the gradients shall not be limited at all.


Better gradients construct better values at the faces resulting in less numerical diffusion.

[Ford Prefect]

Originally Posted by arjun

It is highly connected to numerical diffusion that is associated with advection term that you are considering here. There are many ways it can show up one of them would be to kick in the gradients limiters when the gradients shall not be limited at all.


Better gradients construct better values at the faces resulting in less numerical diffusion.

Yes I completely agree with what you write, but as I wrote, let us consider the standard UD scheme, no need for gradient calculation in that case. Standard UD is the worst scheme when considering numerical diffusion so it seems appropriate to use as a comparison when we talk about tet vs hex vs poly. And since it does not use gradient calculations there is no question about whether it is the advection scheme gradient calculation or if it is the non-orthogonal flow/face alignment that is the main driver for the numerical diffusion. At least in my humble opinion.

Or perhaps I misunderstand your reply in that you mean that numerical diffusion is mainly caused by the gradient calculation? In this case I can show several counter-examples where the numerical scheme has absolutely no effect on the numerical diffusion (my example above was made with UDS and it will produce the same result using 2nd order UD). So I would argue that alignment is the main driver, and in absence of alignment then the scheme becomes more important to reduce numerical diffusion.

[FMDenaro]

Again, "numerical diffusion" is a nomenclature due to the appearence of a diffusion-like term in the modified differential equation, no matter about the type of grid. You need to introduce the scheme to talk about that!



In commercial codes, like Ansys, this nomenclature is used in a misleading way when some advices to users are done about the choice structured vs unstructured grids. That is due to the fact that the choice for the discretization is constrained by at least second order scheme for transient. And such discretization have nothing to do with the modern multidimensional discretization.



Since you are talking about direction of the flow compared to the normal vector unit to the face, I assume you are considering FVM, not FDM. Remember that the update in a cell is due after doing the sum of contribution of the flux along each face. Thus, is not sufficient to consider only the condition for a single face, you should ensure that the flow is aligned to the normal vector unit both for an inflow and outflow faces.



Last note, consider a standard structured grid with a non-uniform step. Write a FD "central" derivative and evaluate the modified wavenumber. You will see the appearence of a imaginary part, that is a dumping in the amplitude, like a numerical diffusion. In this sense, despite the fact that the structured grid is aligned that introduces also on the central scheme the numerical diffusion.

[arjun]

Originally Posted by Ford Prefect

Yes I completely agree with what you write, but as I wrote, let us consider the standard UD scheme, no need for gradient calculation in that case. Standard UD is the worst scheme when considering numerical diffusion so it seems appropriate to use as a comparison when we talk about tet vs hex vs poly. And since it does not use gradient calculations there is no question about whether it is the advection scheme gradient calculation or if it is the non-orthogonal flow/face alignment that is the main driver for the numerical diffusion. At least in my humble opinion.

Or perhaps I misunderstand your reply in that you mean that numerical diffusion is mainly caused by the gradient calculation? In this case I can show several counter-examples where the numerical scheme has absolutely no effect on the numerical diffusion (my example above was made with UDS and it will produce the same result using 2nd order UD). So I would argue that alignment is the main driver, and in absence of alignment then the scheme becomes more important to reduce numerical diffusion.

First order upwind scheme is a special case where gradients are zero.

Second order upwind scheme is better and now gradients are not zero.

Third order upwind scheme is more accurate than the other two and hence has less numerical diffusion. This scheme has more gradient terms.

(this is assuming ideal and most accurate gradients).

Now with wrong and bad gradients both second order and third order schemes could be worse than first order upwind and may (if not wrong) also exhibit numerical diffusion efforts.

[Ford Prefect]

First, thank you for having this discussion, it is interesting!

Originally Posted by FMDenaro

Again, "numerical diffusion" is a nomenclature due to the appearence of a diffusion-like term in the modified differential equation, no matter about the type of grid. You need to introduce the scheme to talk about that!

Since you are talking about direction of the flow compared to the normal vector unit to the face, I assume you are considering FVM, not FDM. Remember that the update in a cell is due after doing the sum of contribution of the flux along each face. Thus, is not sufficient to consider only the condition for a single face, you should ensure that the flow is aligned to the normal vector unit both for an inflow and outflow faces.

In FVM context:

I would argue that numerical diffusion is the erroneous propagation of (advection) information on a fixed eulerian mesh. I think it is unnecessary to talk about the differential equation since we can describe the phenomenon from the flux balance directly, just using numerical reasoning (as opposed to physical reasoning ). Basically, if we have no means of moving information in directions other than the face normal direction (of any face) then we will always cause some numerical diffusion unless the advection velocity is either parallel or orthogonal to each of the faces of the cell. There is a caveat though; as I showed in my example with the triangular mesh, it is fully possible to have zero diffusion even though this constraint is violated. This is because the numerical diffusion caused when leaving the main diagonal (flow vector is not parallel to the face vector) is then corrected in the next triangle.

Originally Posted by FMDenaro

Thus, is not sufficient to consider only the condition for a single face, you should ensure that the flow is aligned to the normal vector unit both for an inflow and outflow faces.

Excellent, this is my point! How do we get this "preferred directions" when considering a polyhedral cell? I cannot see how such a cell can have one inflow face and one outflow face while all other faces are being parallel to the flow direction. Polyhedral cells can probably not be used in the same manner since we cannot fill a hexahedral cell with a number of *standard* polyhedral cells (let's use hexagons for simplicity, I have added a figure to illustrate my point).

Originally Posted by FMDenaro

In commercial codes, like Ansys, this nomenclature is used in a misleading way when some advices to users are done about the choice structured vs unstructured grids. That is due to the fact that the choice for the discretization is constrained by at least second order scheme for transient. And such discretization have nothing to do with the modern multidimensional discretization.

Agreed, it is misleading! It is not only ANSYS though, this is rather widely spread I think.




PS I do think hexagons are good.

[FMDenaro]

Numerical diffusion is not associated to a propagation along a specific path-line as happens in convection but is isotropic. You have to consider the appearence also of more general numerical errors like the dispersion error.


As a more general comments, while the flow of momentum enters into a face of a FV it is simultaneously subject to the physical diffusion and pressure gradient. Thus, it is this kind of combination that has to be described.

In my old experience I found good results on several types of unstructured grids, see Sec.4.1 here
https://www.researchgate.net/publica...cal_Simulation

[Ford Prefect]

Originally Posted by FMDenaro

Numerical diffusion is not associated to a propagation along a specific path-line as happens in convection but is isotropic.

I do not understand this. If numerical diffusion is isotropic then it would also appear across faces that are parallel to the flow direction. Could you explain your statement in the context of my example with triangles in a structured mesh?

Originally Posted by FMDenaro

You have to consider the appearence also of more general numerical errors like the dispersion error.

How does dispersion errors affect the choice of tet vs hex vs poly in terms of numerical diffusion?

[FMDenaro]

Originally Posted by Ford Prefect

I do not understand this. If numerical diffusion is isotropic then it would also appear across faces that are parallel to the flow direction. Could you explain your statement in the context of my example with triangles in a structured mesh?



How does dispersion errors affect the choice of tet vs hex vs poly in terms of numerical diffusion?

Again, without talking about a specific scheme, an aswer to your question has no practical meaning. Numerical diffusion (that, differently from the physical one, can be also non isotropic) is associated to the presence in the modified equation of second derivates while dispersion is associated to third derivatives.

[LuckyTran]

In the context of implicit FVM, when you write down the discretized equations with the discretization schemes, there are terms that are diffusion-like (they look exactly like diffusion) except they don't have their origins in physical diffusion and this we call numerical diffusion. You can appreciate this much easier if you write down the discretized equation using symbols instead of looking at pictures of solved velocity fields. The schemes cause the diffusion so you cannot just simply ignore all the math and say we don't need to talk about differential equations. The mesh also enters here in a generic way since the discretized sccheme will take displacements from mesh. Still there is much more analysis needed to prove why poly vs hex vs tets is better/worse for numerical diffusion for a general class of expected flow.


The easiest example is to apply upwinding to a pure advection equation and write down the symbols by hand. Then you see that discretized (pure advection) equation becomes an advection-diffusion equation. If you need help understanding why numerical diffusion is isotropic I suggest doing a 3D advection equation in vector notation. The equation will be identical for 1D and 3D if you use vector notation and there you can plainly see that it is indeed isotropic.

Not all numerical errors are numerical diffusion. Some common schemes produce spurious oscillations (2nd order upwinding or central difference for example) produce errors that are anti-diffusive (overshoots and undershoots). And to explain what is numerical dispersion: anything that isn't already named like numerical diffusion, whatever is left that is an unnamed error, is numerical dispersion.

[sbaffini]

The simplest example I can think of is linear advection with the FTUS scheme in 1D and uniform grid. What you get is just function of the Courant number and ranges from numerical diffusion to exact transport to instability.

So, it is not, indeed, just about the mesh and flow direction.

[Ford Prefect]

Thank you @arjun, @FMDenaro and @LuckyTran for your input. I hope my answers are not coming off as rude. I think this is interesting and even though I do not agree with your way of explaining why "preferred direction" of poly cells are common in comparisons between tet vs hex vs poly, I now have a few additional comments/questions regarding numerical diffusion, since this is the direction the thread took.

Originally Posted by FMDenaro

Again, without talking about a specific scheme, an aswer to your question has no practical meaning. Numerical diffusion (that, differently from the physical one, can be also non isotropic) is associated to the presence in the modified equation of second derivates while dispersion is associated to third derivatives.

But I have said UDS several times. Please explain it using UDS or pick the scheme you like.

Originally Posted by LuckyTran

In the context of implicit FVM, when you write down the discretized equations with the discretization schemes, there are terms that are diffusion-like (they look exactly like diffusion) except they don't have their origins in physical diffusion and this we call numerical diffusion. You can appreciate this much easier if you write down the discretized equation using symbols instead of looking at pictures of solved velocity fields. The schemes cause the diffusion so you cannot just simply ignore all the math and say we don't need to talk about differential equations. The mesh also enters here in a generic way since the discretized sccheme will take displacements from mesh.

Welcome LuckyTran, we usually disagree, let's see how this goes!



I am not ignoring the math, I just gave an example that really does not need any differential equations. I have full appreciation for the differential equations, especially if we use FDM, but in many cases for FVM they are not needed in order to explain phenomena (imho). I thought it was obvious from figure 3 what I meant. You can see that the information propagation on the triangle mesh is actually causing numerical diffusion, which is corrected thanks to the structure of the mesh. Information (stored at the cell center) is not traveling along the advection direction, but is wiggling up and down. The wiggles cancel out with the current mesh and as such there is no numerical diffusion. I am assuming a steady-state here and transmit information in an iterative manner, but we could discretize time as well to explain similar phenomena in transient calculations.



I also added an example of numerical diffusion, using this reasoning, in the hexagonal example. Here information travels to nodes that are not on the trajectory that any particle starting at the initial node would actually land on if the advection scheme was correct (in reality we obviously need to imagine particles originating from the entire volume of the cell). This causes a smearing of information that I attribute to numerical diffusion. It is also clear that larger cells cause more numerical diffusion, using this reasoning. I could draw another figure where a color function is advected on a mesh to make it even more clear, but I think figure 3 should be clear enough.

Originally Posted by LuckyTran

Still there is much more analysis needed to prove why poly vs hex vs tets is better/worse for numerical diffusion for a general class of expected flow.

Thank you, this is answering my original question. So in conclusion; any text which referees to "preferred directions" as a strong point of polyhedral cells is just marketing talk. They should really stop at "more neighbors which helps with gradient calculations".

[Ford Prefect]

Originally Posted by sbaffini

The simplest example I can think of is linear advection with the FTUS scheme in 1D and uniform grid. What you get is just function of the Courant number and ranges from numerical diffusion to exact transport to instability.

So, it is not, indeed, just about the mesh and flow direction.

It depends how you discretize time. You can imagine a case where we discretize space-time and solve this as any other 2D problem. Then you can use different cell-shapes in time.

[FMDenaro]

I think you are mixing several issues of the numerics.

What you call "numerical diffusion" when talking only about the grid is better analysed if you consider the grid resolution for high/infinite gradient. What happens if you sample an initial Heaviside function on a grid? There is no way to describe exactly the singularity, you have only the information that you have the value 1 on a node and 0 on the next. You have lost any information between 1 and 0 and that is consistent to the fact you accept a regular function between the two nodes. This is a sort of "numerical diffusion", without talking about any scheme.
But, formally, this is the sampling error you have due to the Nyquist theorem.


Then, if you consider a physical reasoning in a FV, also at a steady state, the balance of the fluxes means nothing. You can have a balance also if you have convective and diffusive fluxes.



In this old paper
https://www.sciencedirect.com/scienc...21999179901426


you can see a proposal for a multidimensional scheme with an anisotropic diffusion with the goal of reducing the numerical viscosity of the donor cell.

[sbaffini]

Originally Posted by Ford Prefect

It depends how you discretize time. You can imagine a case where we discretize space-time and solve this as any other 2D problem. Then you can use different cell-shapes in time.

I don't think I understand. I referred to Forward in Time Upwind Scheme as method, which means explicit euler in time (and I assumed constant time steps, of course).

But that's not the point. What I wanted to highlight is that you can have the simplest convection scheme EVER on the simplest grid arrangement to behave in whatever way you like just using a different time step (which in your 2D view would be the 2D grid aspect ratio).

So, the point is, numerical diffusion is either there or it isn't. Flow alignment can, indeed, remove ADDITIONAL numerical diffusion terms, but not change the nature of the scheme.

In general, flow alignment is related to the fact that certain solution derivatives are 0 in a certain frame of reference. As a consequence, the resulting terms in the Modified Differential Equations are locally 0 and the resulting error, which is still dependent on the scheme, is lower.

Hexa grids are naturally inclined to this (pun intended). Polyhedral and tetrahedral grids are not, to the best of my knowledge.

Where polys should be better than tetra (but not properly aligned hexa) is error cancellation on opposite faces and, as mentioned by arjun, gradient computation. But, honestly, I haven't seen a verified statement for none of them. After all, polyhedral grids are mostly an exclusive of commercial grid generators.

[LuckyTran]

There are certain advantages to polyhedral and hexahedral meshes over tetrahedral meshes, it is not just some stupid marketing guy that came up with it. But you need to first understand what is numerical diffusion and what is not.

Do a taylor series about the face flux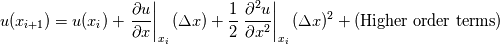



Upwinding means we approximate the derivative as such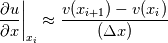


Therefore when you solve using this upwind scheme, you don't solve for the true velocity u, but a modified velocity v which contains numerical diffusion because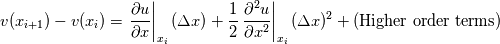


If you want to see numerical dispersion then do the taylor series to the next higher order term (hint: keep the 3rd order derivative).

Here you see different grids that weakly produce different v's even without needing any actual gradient calculation for the same prototype upwind scheme will have differing amounts of numerical diffusion, it just depends how close v is to the actual u. Not shown here is that a tet grid vs a hex grid vs a poly grid, one is more accurate than another. I've shown it for 1 face flux. You need to sum the fluxes over all cells. Here is where the cell type matters because you can have error cancellation depending on the cell type and the scheme.

[Ford Prefect]

Trying to reply to portions of the text since there are many new concepts being introduced to the discussion.

Originally Posted by FMDenaro

I think you are mixing several issues of the numerics.

Then, if you consider a physical reasoning in a FV, also at a steady state, the balance of the fluxes means nothing. You can have a balance also if you have convective and diffusive fluxes.

I am not talking about the flux balance. I am talking about the discrete nature of only transmitting information in the normal direction of cell faces. Take chess as an analogy. The bishop can move in a way the rook cannot. FVM is the rook equivalent to information propagation. The problem is that if we have oblique flow in FVM then we will cut the rook in a couple of pieces and send it both in the horizontal and in the vertical directions (still while maintaining conservation since fractured pieces of rook will enter through the opposing sides, but this is not the point).

Originally Posted by sbaffini

I don't think I understand. I referred to Forward in Time Upwind Scheme as method, which means explicit euler in time (and I assumed constant time steps, of course).

But that's not the point. What I wanted to highlight is that you can have the simplest convection scheme EVER on the simplest grid arrangement to behave in whatever way you like just using a different time step (which in your 2D view would be the 2D grid aspect ratio).

Yes, FTUS can be seen as a (in context of FVM) discretization of space-time where we use a downwind approximation in time (for explicit treatment, for implicit treatment we use upwind in time). Normally we do not discretize and solve for space-time since that would force us to use an extremely expensive 3D calculation (3D space + time). Solving for space-time in 1D (1D space+time) cases is easy though. All such solvers would not step in time but rather solve as if the case is "steady-state".


It is easy to see that you can create a space-time mesh that satisfies the Courant number constraint given by traditional analysis.

Originally Posted by sbaffini

So, the point is, numerical diffusion is either there or it isn't. Flow alignment can, indeed, remove ADDITIONAL numerical diffusion terms, but not change the nature of the scheme.

This may be the key point. Would you say that the triangle example above has numerical diffusion?