Best practice guidelines for turbomachinery CFD
From CFD-Wiki
| Line 188: | Line 188: | ||
Discretization errors can either be spatial errors in space or temporal errors in time. | Discretization errors can either be spatial errors in space or temporal errors in time. | ||
| - | Spatial discretization errors are what people normally call discretization errors. These errors are due to the difference between the exact solution and the numerical representation of the solution i space. Describing exactly which discretization all different codes have is not possible here. Instead some general rules to avoid these errors can be summarized as: | + | Spatial discretization errors are what people normally call discretization errors. These errors are due to the difference between the exact solution and the numerical representation of the solution i space. Describing exactly which discretization all different codes have and what errors this might lead to is not possible here. Instead some general rules to avoid these errors can be summarized as: |
| - | # Use at least a 2nd order accurate scheme, preferably a 3rd order accurate scheme. | + | # Use at least a 2nd order accurate scheme, preferably a 3rd order accurate scheme. Some general purpose codes have a 1st order upwind scheme as default, this is a very diffusives schemes that often gives too smooth results. |
# For new applications always run a simulation with a finer mesh to see how grid independent your solution is. | # For new applications always run a simulation with a finer mesh to see how grid independent your solution is. | ||
| - | # Be aware of checker-board errors. | + | # Be aware of checker-board errors. Checker-board errors occur close to strong shocks and other large discontinuities and can be seen as a wavy pattern with a wavelength of two cells. Some schemes, especially those who behave like central differencing schemes, are more prone to checker-board errors. Upwind schemes are a bit better and schemes like TVD or chock-capturing schemes are even better. |
| + | |||
| + | Temporal discretization errors mainly effect transient simulations. However, some codes use a time-marching method also for steady simulations and then a temporal discretization error might affect the final steady solution slightly. The discretization in time can be done with 1st or 2nd order schemes or a Runge-Kutta method, which is more accurate and saves memory. Some codes can adapt the time-step, but often it is necessary to prescribe a time-step in advance. Think of the time-step as your grid in time and make sure that the grid-resultion in time is fine enough to resolve the highest fequencies. To avoid problems with temporal discretization errors the following should be considered: | ||
| + | # Use at least a 2nd order scheme in time. | ||
| + | # Do a physical estimation of the typical frequencies in time of the phenomena that you are interested in and select a time-step which is fine enough to resolve these frequencies well. After the simulation also look at the frequencies captured and make sure that they are well resolved by the chosen time-step. | ||
| + | # For new applications try a finer time-step to ensure that your solution in time is fairly grid independent in time. | ||
==== Convergence errors ==== | ==== Convergence errors ==== | ||
Revision as of 09:29, 3 May 2007
This article contains a summary of the most important knowledge and experience a CFD engineer needs in order to perform CFD simulations of turbomachinery components. The guide is mainly aimed at axial turbomachinery. The goal is to give a CFD engineer, who has just started working with turbomachinery simulations, a head start and avoid some of the most difficult pit-falls. Experienced turbomachinery CFD engineers can also use the guidelines in order to learn what other experts consider best practice. The intended audience is expected to know basic CFD terminology and have a basic turbomachinery knowledge, but no detailed knowledge about CFD for turbomachinery is needed.
Deciding what type of simulation to do
2D, Quasi-3D or 3D
2D simulations are often used in the early design phase in order to obtain a typical 2D section of a blade. For cases with many long blades or vanes, like low-pressure turbines, a 2D simulation can also provide reasonable results. If the area of the flow-path changes significantly in the axial direction it might be necessary to instead make a Quasi-3D simulation. A quasi-3D simulation is a 2D simulation in which extra source terms are used to account for the acceleration/decelleration caused by a changing channel height or growing endwall boundary layers. Codes focused on turbomachinery applications often have the possibility to perform quasi-3D simulations, but most general purpose commercial CFD codes can not do this type of simulations, or require user coding to implement the correct source terms in the equations. Please contact your software distributor if your code does not have this possibility and you require it. Many codes require special routines or hidden commands to enable the quasi-3D feature.
Full 3D simulations are necessary if a true 3D geometry is needed to obtain correct secondary flows and/or shock locations. For low-aspect-ratio cases with only a few short blades, like for example structurally loaded turbine outlet guide vanes, the secondary flow development is important and a 3D simulation is often necessary in order to obtain reasonable results. For applications where the endwall boundary layers grow very quickly and interact with a large part of the flow-field it is necessary to perform a full 3D simulation. This is often the case in compressors and fans, where the negative pressure gradients make the boundary layers grow much quicker than what they do in for example turbines. For cases where the shock location is very critical, like in transonic compressors, it is also often necessary to perform a 3D simulation in order to obtain reasonable shock locations.
Inviscid or viscid
For attached flows close to the design point and without any large separations it is often sufficient with an inviscid Euler simulation in order to obtain reasonable blade loadings and pressure distributions. Note that inviscid Euler simulations should only be used if the boundary layers are judged to not have a significant effect on the global flow-field. A viscid Navier-Stokes simulation is necessary in order to predict losses, secondary flows and separations. As soon as separations are of interest it is of course also necessary to do a viscid simulation.
Transient or Stationary
Most turbomachinery simlation are performed as stationary simulations. Transient simulations are done when some kind of transient flow behaviour has a strong influence on the global flow field. Examples of transient simulations are detailed simulations of rotor-stator interaction effects, simulations of large unsteady separations etc. Sometimes when you perform a steady stationary simulation you can see tendencies of unsteady behvaiour like for example periodic vortex shedding behind blunt trailing edges. This is often first seen as periodical variations of the residuals. If the unsteady tendencies are judged to not affect the overall simulation results if might be necessary to coarsen the mesh close to the vortex shedding or run a different turbulence model in order to make the simulation converge. Sometimes you are still forced to run a transient simulation and average the results if you don't obtain a converged steady solution.
Meshing
In turbomachinery applications structured muli-block hexahedral meshes are most often used for flow-path simulations. In most solvers a structured grid requires less memory, provides superior accuracy and allows a better boundary-layer resolution than an unstructured grid. By having cells with a large aspect ratio around sharp leading and trailing edges a structured grid also provides a better resolution of these areas. Many companies have automatic meshing tools that automatically mesh blade sections with a structured mesh without much user intervention.
Unstructured meshes are used for more complex and odd geometries where a structured mesh is difficult to create. Typical examples where unstructured meshes are often used are blade tip regions, areas involving leakage flows and secondary air systems, film cooling ducts etc.
Mesh size guidelines
It is difficult to define, a priori, the mesh size. The required mesh size depends on the purpose of the simulation.
If the main goal is to obtain static pressure forces a coarse mesh is often able to obtain a good solution, especially when an accurate resolution of the boundary layers is not required. For 2D inviscid simulations of one blade a mesh with say 3,000 cells is most often sufficient. For 3D inviscid blade simulations a mesh size of about 40,000 cells is usually sufficient. On inviscid Euler simulations the cells should be fairly equal in size and no boundary layer resolution should be present. Avoid having too skewed cells.
For loss predictions and cases where boundary layer development and separation is important the mesh needs to have a boundary layer resolution. The boundary layer resolution can either be coarse and suitable for a wall function simulation or very fine and suitable for a low-Re simulation. For further information about selecting the near-wall turbulence model please see the turbulence modeling section. In 3D single-blade simulations a decent wall-function mesh typically has around 100,000 cells. This type of mesh size is suitable for quick design iterations where it is not essential to resolve all secondary flows and vortices. A good 3D wall-function mesh of a blade section intended to resolve secondary flows well should have at least 400,000 cells . A good low-Re mesh with resolved boundary layers typically has around 1,000,000 cells.
In 2D blade simlations a good wall-function mesh has around 20,000 cells and a good low-Re mesh with resolved boundary layers has around 50,000 cells.
Along the suction and pressure surfaces it is a good use about 100 cells in the streamwise direction. In the radial direction a good first approach is to use something like 30 cells for a wall-function mesh and 100 cells for a low-Re mesh.
It is important to resolve leading and trailing edges well. Typically at least 10 cells, preferably 20 should be used around the leading and tralining edges. For very blunt and large leading edges, like those commonly found on HP turbine blades, 30 or more cells can be necessary.
Cases which are difficult to converge with a steady simulation and which show tendencies of periodic vortex shedding from the trailing edge, can sometimes be "tamed" by using a coarse mesh around the trailing edge. This, of course, reduces the accuracy but can be a trick to obtain a converged solution if time and computer resouces does not allow a transient simulation to be performed.
Boundary layer mesh
For design iteration type of simulations where a wall function approach is sufficient y+ for the first cell should be somewhere between 20 and 200. The outer limit is dependent on the actual Re number of the simulations. For cases with fairly low Re numbers make sure to keep the maximum y+ as low as possible. For more accurate simulations with resolved boundary layers the mesh should have a y+ for the first cell which is below 1. Some new codes are now using a hybrid wall treatment that allows a smooth transition from a coarse wall-function mesh to a resolved low-Re mesh. Use some extra care when using this type of hybrid technique since it is still fairly new and unproven.
Otside of the first cell at a wall a good rule of thumb is to use a growth ratio normal to the wall in the boundary layer of maximum 1.25. For a low-Re mesh this usually gives around 40 cells in the boundary layer whereas a wall-function mesh does not require more than 10 cells in the boundary layer.
If you are uncertain of which wall distance to mesh with you can use a y+ estimation tool to estitmate the distance needed to obtain the desired y+. These estimation tools are very handy if you have not done any previous similar simulations.
As a rule of thumb a wall-function mesh typically requires areound 5 to 10 cells in the boundary layer whereas a resolved low-Re mesh requires about 40 cells in the boundary layer.
Boundary conditions
Describe different types of boundary conditions and when they should be used:
- Total pressure in, static pressure out
- Absorbing boundary conditions
- ...
Turbulence inlet conditions
Prescribing realistic turbulence inlet conditions is important and usually difficult. For two-equation turbulence models two different turbulence values need to be specified on the inlet. The most common way of specifying the inlet turbulence variables is to give an inlet turblence level and length-scale. For simulations where the incoming boundary layers are estimated to not have any significant effect on the secondary flows and global flow-field downstream it is usually sufficient to specify a constant incoming turbulence level and length-scale.
The incoming turbulence level is dependent on which component is analyzed. Best is of course to have measurments from a similar application in order to be able to prescribe a fairly realistic value. Without measurements it is necessary to make an educated guess. Simulations with very complex and turbulence-generating components upstream will have a very high incoming turbulence level. For example, a high-pressure turbine just downstream of a turbulence generating combustor might have incoming turbulence levels up to 20%. Fans and low-pressure compressors with not many components upstream might have as low incoming turbulence level as 1%. For components between these two extreme examples, like high-pressure compressors, low-pressure turbines etc. a turbulence level of around 5% might be realistic. If you do not have any measurements and are unsure about which incoming turbulence level to prescribe it is always a good idea to run a few different simulations with say one half and one double incoming turbulence level in order to estimate how important it is for the simulation results.
The incoming turbulence length-scale is often even more difficult to guess than the incoming turbulence level. Measurements might sometimes include the incoming turbulence level, but very seldom also include the incoming turbulent length-scale. The best way of guessing a realistic incoming length-scale is to use the geometrical properties of the upstream components. The incoming turbulence length-scale can be estimated as say the thickness of upstream blades or somewhere between 2% and 20% of the incoming channel heigth. Fortunately the incoming turbulence length-scale is usually not that important for the end results. However, some k-omega models can have an unrelisticly strong influence on the incoming turbulence length-scale. Hence, be extra carefull about the length-scale when using k-omega models. Note that the SST k-omega model does not have this unrealistic sensitivity to the inlet turbulence length-scale.
Instead of specifying an incoming turbulence length-scale it is sometimes more convenient to specify an incoming eddy viscosity ratio. For low-turbulence cases with no well-specified turbulence generating components upstream it can be difficult to estimate a turbulence length-scale. Specifying an eddy viscosity ratio instead gives a more direct control over how large the effect of the incoming turbulence is. The eddy viscosity ratio describes how large the turbulence viscosity is related to the molecular viscosity. In turbomachinery the eddy viscosity ratio can vary from say 10 in low-turbulence components like fans up to say 1,000 or in rare cases even 10,000 in high-turbulence components like high-pressure turbines. In components between these extremes a typical eddy viscosity ration might be about 200. Even if specifying an inlet turbulence length scale it can still be good to compute what eddy viscosity ratio this corresponds to in order to estimate if it sounds reasonable.
Turbulence modeling
Selecting a suitable turbulence model for turbomachinery simulations can be a challenging task. There is no single model which is suitable for all types of simulations. Which turbulence model CFD engineers use has as much to do with beliefs and traditions as with knowledge and facts. There are many diffrent schools. However, below follows some advices that most CFD engineers in the turbomachinery field tend to agree upon.
For attached flows close to the design point a simple algebraic model like the Baldwin-Lomax model can be used. Another common choice for design-iteration type of simulations is the one-equation model by Spalart-Allmaras. This model has become more popular in the last years due to the many inherent problems in more refined two-equation models. The big advantage with both the Baldwin-Lomax model and the Spalart-Allmaras model over more advanced models is that they are very robust to use and rarely produce completely unphysical results.
In order to accurately predict more difficult cases, like separating flows, rotating flows, flows strongly affected by secondary flows etc. it is often necessary to use a more refined turbulence model. Common choices are two-equation models like the 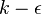 model.
model.
Two-equation models are based on the Boussinesq eddy viscosity assumption and this often leads to an over-production of turbulent energy in regions with strong acceleration or deceleration, like in the leading edge region, regions around shocks and in the suction peak on the suction side of a blade. To reduce this problems it is common to use a special model variant using, for example, Durbin's realizability constraint or the Kato-Launder modification. Note that different two-equation models behave differently in these problematic stagnation and acceleration regions. Worst is probably the standard 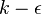 model.
model. 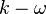 model are slightly better but still do not behave well. More modern variants like Menter's SST k-omega model also has problems, wheras the v2f model by Durbin behaves better.
model are slightly better but still do not behave well. More modern variants like Menter's SST k-omega model also has problems, wheras the v2f model by Durbin behaves better.
Near-wall treatment
For on-design simlations without any large separated regions it is often sufficient to use a wall-function model close to the wall, preferably with some form of non-equilibrium wall-function that is sensitised to streamwise pressure gradients.
For off-design simulation, or simulations involving complex secondary flows and separations, it is often necessary to use a low-Re model. There exists many low-Re models that have been used with success in turbomachinery simulations. A robust and often good choice is to use a one-equation model, like for example the Wolfstein model, in the inner parts of the boundary layer. There are also several Low-Re 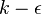 models that work well. Just make sure they don't suffer from the problem with overproduction of turbulent energy in regions with strong acceleration or deceleration. In the last few years Menter's low-Re
models that work well. Just make sure they don't suffer from the problem with overproduction of turbulent energy in regions with strong acceleration or deceleration. In the last few years Menter's low-Re 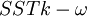 model has gained increased popularity.
model has gained increased popularity.
Transition prediction
Transition refers to the process when a laminar boundary layer becomes unstable and transitions to a turbulent boundary layer. There are two types of transition - natural transition, where inherent instabilities in the boundary layer cause the transition and by-pass transition, where convection and diffusion of turbulence from the free-stream into the boundary layer cause the transition.
Simulating transition in a CFD code accurately is very difficult. Often a separate transition model needs to be solved in order to specify the transition location and length. Predicting natural transition in a pure CFD code is not possible. Predicting by-pass transition in a pure CFD code is almost impossible, although there are people who claim to be able to predict by-pass transition with low-Re two-equation models. However, this is usually on special test cases and with simulations that have been tuned for these special cases, see for example [Saville 2002]. In reality transition is a very complex and sensitive process where disturbances like incoming wakes and vortices from previous stages, surface roughness effects and small steps or gaps in the surfaces play a significant role.
The turbomachinery codes that have transition prediction models often use old ad-hoc models like the Abu-Ghannam and Shaw model [Abu-Ghannam 1980] or the Mayle model [Mayle 1991]. These models can be quite reliable if they have been validated and tuned for a similar application. Do not trust your transition predictions without having some form of experimental validation. Menter has also recently developed a new form of transition model that might work fairly well, but it is still too new and untested.
For some turbomachinery applications, like modern high-lift low-pressure turbines, transition is critical. For these applications a CFD code with a transition model that has been tuned for this type of applications should be used.
Numerical considerations
Use at least a second order accurate scheme for the flow variables. Some codes require a first order scheme for the turbulent variables (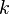 and
and  ) in order to converge well. It might be sufficient with a first order scheme only on the turbulence variables, but a second order scheme is of course preferable.
) in order to converge well. It might be sufficient with a first order scheme only on the turbulence variables, but a second order scheme is of course preferable.
Convergence crieteria
To know when a solution is converged is not always that easy. You need some prior experience of your CFD code and your application to judge when a simulation is converged. For normal pure aero simulations without resolved walls, i.e. with wall functions or inviscid Euler simulations, convergence can most often be estimated just by looking at the residuals. Exacty what the residuals should be is not possible to say, it all depends on how your particular code computes and scales the residuals. Hence, make sure to read the manuals and plot the convergence of a few global parameters before you decide what the residuals should be for a solution to converege. Note also that many manuals for genereal purpose CFD codes list overly agressive convergence critera that often produce uncoverged results. For simulations with resolved walls it is good to look at the convergence of some global properties, like total pressure losses from the inlet to the outlet. For heat transfer simulations it is even more tricky since the aerodynamic field can look almost converged although the thermal field is not converged at all. If doing heat transfer simulations make sure to plot the heat-transfer, run for some time, and plot it again to make sure that it doesn't change anymore. With very well resolved walls and heat transfer it can sometimes take 10 times longer for the thermal field to converge.
Single or double precision
With todays computers and cheap memory prices it often does not cost much extra to run in double precision. Before using single precision you should first investigate how your software and hardware works with double precision. If the extra time and memory needed for double precision is negligible you should of course always run in double precision. With double precision you never have to worry about round-off errors. Always using double precision is one way of avoiding one type of pit-falls in the complex world of CFD simulations. Use double precision when you have resolved boundary layers (Y+ around 1) and when you use advanced physical models like combustion, free-surface simulations, spray and transient simulations with quick mesh motions.
Multi-stage analysis
Types of analysis:
- Frozen rotor
- Frozen rotor defines the domain interface to transfer flow and thermal data across the interface between the stationary and rotating domain. Frozen rotor interface connects the two doamins (rotating and stationary) in such a way that these two domains have a fixed relative position throughout the solution, but with desired frame transformation occurring across the interface. Transient effects cannot be modelled with this interface. This the the only disadvantage of the frozen rotor interface.
- Mixing-plane
In the Mixing-plane also called as "Stage-Interface" approah in the commercial code CFX, variables are circumferentially averaged before passing from one domain to the other, say for instance from stator to rotor. This is used typically when there are blade rows on either sides of the interface. The advantage in this approach is that only one blade passage need to be modeled. One situation where this is less appropriate is while simulating impeller and a volute in a pump/ compressor. Transient effects are completely ignored and often this approach closely matches test data near design point.
- Sliding-mesh
- Time-inclinded
- Adamszyk stresses ...
Describe how to scale blade-sections when doing sliding-mesh computations
Heat transfer predictions
Acoustics and noise
A whole separate research subject, difficult.
Tone noise possible. Often run with linearzised solvers in the frequency domain.
Jet noise possible. Often run with LES or DES simulations that either also resolve the sound waves or couples to a separate acoustic solver.
Turbomachinery broadband noise not possible yet, or at least a great challenge.
Errors and uncertainties
CFD is still a tool which requires that a user has a good understanding of uncertainties and errors that might spoil a CFD similation. There exists no error control in CFD and any CFD simulation must be interpreted by an expirenced user to have some credibility. Without some knowledge about possible errors and how they can be handled a CFD simulation can not be trusted. Errors can occur at different places:
- Definition of the problem - What needs to be analyzed?
- Selection of the solution strategy - What physical models and what numerical tools should be used?
- Development of the computational model - How should the geometry and the numerical tools be set up?
- Analysis and interpretation of the results - How should the model be analyzed and the results be interpreted?
There exists many different definitions on errors. In this guide the errors are classified into four types of errors: problem definition errors, model errors, numerical errors and user and code errors. The chapters below describe these errors and give some guidelines on how to avoid them.
Problem definition errors
Problem definition errors are the most basic form of errors. In order to obtain usefull results a CFD simulation must of course analyze the correct problem, have suitable boundary contions and be based on a relevant geometry.
Wrong type of simulation
It is essential to have an overview of the physics involved and how the problem can best be analyzed. Running a 2D simulation in order to understand secondary flows or running a steady simulation in order to understand transient behaviour is of course no use. When assessing a CFD simulation the first thing to consider is what physical phenomena are important for the results and if the selected type of simulation is suitable to resolve this type of phenomena. For further information about selecting the most suitable type of simulation please see the previous chapeter on deciding what type of simulation to perform.
Incorrect or uncertain boundary conditions
A common source of errors is that incorrect boundary conditions are used. The boundary conditions must be specified in enough detail in order to resolve all the important physical features in the problem. For further information about specifying boundary conditions please see the previous chapter on boundary conditions.
Geometrical errors
It is almost always necessary to simplify the geometry in some form. When assessing a CFD simulation one should consider how the geometrical simplifications can affect the interesting physical phenomena. Typical geometrical errors are:
- Simplifications
- Small geometrical features like fillets, small steps or gaps etc. can often be disregarded. When disregarding this type of features one should consider if they might affect the important physics. For example, a very large fillet on the suction-side of a vane might affect corner separations near the end-walls. A large tip-leakage might affect the flow physics significantly in the upper part of a compressor.
- Tolerances and manufacturing discrepancies
- If the geometry has very large tolerances or is manufactured in a way which might produce a non-ideal shape or position it might be necessary to perform additional CFD simulations in order to cover the whole span of possible real geometries.
- Surface conditions - roughness, welds, steps, gaps etc.
- Often CFD simulations assume a perferctly smooth surface. A non-smooth surface which might have welds, steps or even gaps will of course produce different results. If the physical phenomena of intetrest might depend on the surface conditions these should of course be condidered. Typical phenomena that might be dependent on this type of errors are transition prediction, leakage flows etc.
Model errors
Errors related to the computational model.
Wrong physical models
Once the type of similation has been selected the next step is to select what type of physical models the simulation should use. The following points should be considered:
- Gas data (incompressible/compressible, perfect gas/real gas, ...)
- Turbulence modeling (type of model, type of near-wall treatment, ...)
- Other models (combustion, sprays, ...)
When assessing model related errors it is important to know the features of the selected model and think carefully how these features and possible short comings might affect the predicted physical behaviour.
Numerical errors
Errors related to the numercial solution of the developed model. Typical examples of numerical errors are discretization errors, convergence errors and round-off errors.
Discretization errors
Discretization errors can either be spatial errors in space or temporal errors in time.
Spatial discretization errors are what people normally call discretization errors. These errors are due to the difference between the exact solution and the numerical representation of the solution i space. Describing exactly which discretization all different codes have and what errors this might lead to is not possible here. Instead some general rules to avoid these errors can be summarized as:
- Use at least a 2nd order accurate scheme, preferably a 3rd order accurate scheme. Some general purpose codes have a 1st order upwind scheme as default, this is a very diffusives schemes that often gives too smooth results.
- For new applications always run a simulation with a finer mesh to see how grid independent your solution is.
- Be aware of checker-board errors. Checker-board errors occur close to strong shocks and other large discontinuities and can be seen as a wavy pattern with a wavelength of two cells. Some schemes, especially those who behave like central differencing schemes, are more prone to checker-board errors. Upwind schemes are a bit better and schemes like TVD or chock-capturing schemes are even better.
Temporal discretization errors mainly effect transient simulations. However, some codes use a time-marching method also for steady simulations and then a temporal discretization error might affect the final steady solution slightly. The discretization in time can be done with 1st or 2nd order schemes or a Runge-Kutta method, which is more accurate and saves memory. Some codes can adapt the time-step, but often it is necessary to prescribe a time-step in advance. Think of the time-step as your grid in time and make sure that the grid-resultion in time is fine enough to resolve the highest fequencies. To avoid problems with temporal discretization errors the following should be considered:
- Use at least a 2nd order scheme in time.
- Do a physical estimation of the typical frequencies in time of the phenomena that you are interested in and select a time-step which is fine enough to resolve these frequencies well. After the simulation also look at the frequencies captured and make sure that they are well resolved by the chosen time-step.
- For new applications try a finer time-step to ensure that your solution in time is fairly grid independent in time.
Convergence errors
Round-off errors
When using single precision care needs to be taken to avoid round-off errors. Inviscid Euler simulations and simulations using wall-function meshes can most often be performed in single precision. For well resolved boundary layers with Y plus close to 1 it is often necessary to use double precision. If using double precision for very fine mesh resolutions make sure that you also create the mesh in double precision and not just run the solver in double precision. Sometimes a single precision solver converges slower than a double precision solver due to numerical errors caused by round-off errors. When using advanced physical models like combustion, free-surface simulations, spray and transient simulations with quick mesh motions it is also often necessary to use double precision.
User and code errors
Errors related to bugs in the code used or misstakes made by the CFD engineer.
What to trust and what not to trust
CFD is generally quite good at predicting surface static pressure distributions. With care CFD can also be used to predict performance, total-pressure losses and blade turning.
Predicting separation, stall and off-design performance can be a challenge and results with non-attached flows should be interpreted with care.
Heat transfer is often very difficult to predict accurately and it is common to obtain heat-transfer coefficients that are 100% wrong or more. Validation data is critical in order to be able to trust heat transfer simulations.
Transition is almost impossible to predict accurately in general. However, there exist models that have been tuned to predict transition and these tend to give acceptable results for cases close to the ones they were tuned for.
References
- Abu-Ghannam, B.J. and Shaw, R. (1980), "Natural Transition of Boundary Layers - the Effects of Turbulence, Pressure Gradient, and Flow History", Journal of Mech. Eng. Science, vol. 22, no. 5, pp. 213–228.
- Baldwin, B. S. and Lomax, H. (1978), "Thin Layer Approximation and Algebraic Model for Separated Turbulent Flows", AIAA Paper 78-257.
- Menter, F.R. (1994), "Two-equation eddy-viscosity turbulence models for engineering applications", AIAA Journal, vol. 32, pp. 269-289.
- Mayle, R. E. (1991), "The Role of Laminar-Turbulent Transition in Gas Turbine Engines", ASME Journal of Turbomachinery, vol. 113, pp. 509-537.
- Savill, M., Dick, E., Hanjalić, K. and Voke, P. (2002), "Synthesis Report of the ERCOFTAC Transition Modeling – TRANSPRETURB Thematic Network Acitivities 1998-2002", Ecoftac Bulletin 54, September 2002, pp. 5-16.
External links
QNET-CFD Best Practise Advice for Turbomachinery Internal Flows
