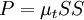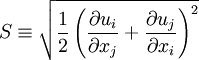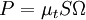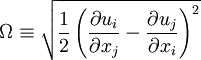Kato-Launder modification
From CFD-Wiki
The Kato-Launder modification is an ad-hoc modification of the turbulent production term in the k equation. The main purpose of the modification is to reduce the tendency that many two-equation models have to over-predict the turbulent production in regions with large normal strain, i.e. regions with strong acceleration or decelleration.
Contents |
Basic equations
Following the CFD-Wiki article on low-Re k-epsilon models the transport equation for the turbulent energy, 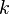 , used in most two-equation models can be written as:
, used in most two-equation models can be written as:
Where 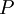 is the turbulent production normally given by:
is the turbulent production normally given by:
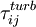 is the turbulent shear stress tensor given by the Boussinesq assumption:
is the turbulent shear stress tensor given by the Boussinesq assumption:
Where 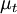 is the eddy-viscosity given by the turbluence model and
is the eddy-viscosity given by the turbluence model and 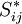 is the trace-less viscous strain-rate defined by:
is the trace-less viscous strain-rate defined by:
In incompressible flows, where 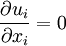 , the production term
, the production term 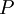 can be rewritten as:
can be rewritten as:
Hence
Where
Production term modification
The proposal by Kato and Launder is to replace one of the strain-rates, 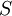 , in the turbulent production term with the vorticity,
, in the turbulent production term with the vorticity, 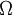 . The Kato-Launder modified production then becomes:
. The Kato-Launder modified production then becomes:
Where
and
Applicability
The Kato-Launder modification can be used together with most two-equation models that have a production term formulated as above. The modification was originally developed for transient simulations of vortex-shedding behind square cylinders, where the normal k-epsilon model tends to produce too much turbulent energy in stagnation regions and in the small regions with strong acceleration and decelleration around the square corners. This over-production create too much turbulent viscosity which in turns affects the vortex-shedding and the development of the vortex-street downstream of the square cylinder. With the modified production term Kato and Launder was able to produce much better results.
The Kato-Launder modification has also been popular in the turbomachinery field, where the stagnation-point-problem of two-equation models can lead to significant errors. In these applications it is common with regions with very high acceleration and decelleration (leading edges, shocks, suction-side peaks, ...) where the Kato-Launder modification can improve the results with a two-equation model which otherwise predicts too much turbulence. Lately the popularity of the Kato-Launder modification has decreased though. Instead people are using more modern models that inherently have limiters and relizability constraints that reduce the stagnation-point problem.
Discussion
In pure shear-flows like boundary-layers and wakes the Kato-Launder modified production term will give exactly the same result as the unmodified production term. However, outside of boundary-layers and wakes the Kato-Launder modified production term will give very different results. Essentially what it does is to turn off the turbulent production outside of boundary-layers and wakes. This has the good effect that the over-production of turbulent energy in stagnation regions and regions with very strong acceleration is eliminated. The downside is that turning off the turbulent production is not exactly accurate either. For example, the Kato-Launder modification will give too low turbulence levels in stagnation regions and this in turn will affect heat-transfer and skin-friction around the stagnation point.
Model variants
There are a few variations on the Kato-Launder modification where the production term is written as a linear combination of the unmodified production term and the Kato-Launder modified production term. These models were developed with the intention of combining the best of both sides. They never became very popular though and are now rarely used.
References
Kato, M. and Launder, B. E. (1993), "The Modeling of Turbulent Flow Around Stationary and Vibrating Square Cylinders", Proc. 9th Symposium on Turbulent Shear Flows, Kyoto, August 1993, pp. 10.4.1-10.4.6.

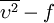 model
model
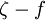 model
model
![\frac{\partial}{\partial t} \left( \rho k \right) +
\frac{\partial}{\partial x_j}
\left[
\rho k u_j - \left( \mu + \frac{\mu_t}{\sigma_k} \right)
\frac{\partial k}{\partial x_j}
\right]
=
P - \rho \epsilon - \rho D](/W/images/math/8/d/7/8d787db6600e44ff6855992620431595.png)
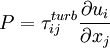
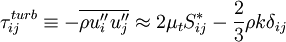
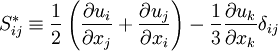
![\begin{matrix}
P & = & \tau_{ij}^{turb} \frac{\partial u_i}{\partial x_j} \\
\ & = & \left[ 2 \mu_t S_{ij}^* - \frac{2}{3} \rho k \delta_{ij} \right] \frac{\partial u_i}{\partial x_j} \\
\ & = & \left[ 2 \mu_t \left( \frac{1}{2} \left(\frac{\partial u_i}{\partial x_j} +
\frac{\partial u_j}{\partial x_i} \right) - \frac{1}{3} \frac{\partial u_k}{\partial x_k} \delta_{ij} \right)
- \frac{2}{3} \rho k \delta_{ij}
\right] \frac{\partial u_i}{\partial x_j} \\
\ & \approx & \mu_t \left(\frac{\partial u_i}{\partial x_j} +
\frac{\partial u_j}{\partial x_i} \right) \frac{\partial u_i}{\partial x_j} \\
\ & = & \mu_t \frac{1}{2} \left(\frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right)
\left(\frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) \\
\end{matrix}](/W/images/math/c/2/e/c2edca17cad100ee94b91f1ebc9516c5.png)