 |
|
|
[Sponsors] | |||||
LES of Turbulent Channel Flow; increased flux for some models? |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Join Date: Nov 2014
Posts: 9
Rep Power: 11  |
Hi everybody!
I am currently doing Large Eddy Simulation for the case of fully developed turbulent channel flow for a selection of Reynolds numbers. I have experienced some weird behaviour with the simulations, and I would like to check if anyone here has a solution or an explanation regarding this behaviour. The case is set up with a constant pressure gradient equal to 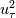 as a forcing term, no constant flux is imposed on the flow as traditionally is done by e.g. Moser, Kim and Mansour in their paper. Hence the computation is carried out until a steady mass flux is obtained (higher than what is obtained by DNS), then the sampling of data is started. as a forcing term, no constant flux is imposed on the flow as traditionally is done by e.g. Moser, Kim and Mansour in their paper. Hence the computation is carried out until a steady mass flux is obtained (higher than what is obtained by DNS), then the sampling of data is started.So, the thing is, for all turbulent Reynolds numbers the over dissipative Smagorinsky model works very well. It's like pulling the handbrake, the obtained mean velocity profiles are much closer to the DNS profiles, with erroneus results in wall regions. Activating this model reduces the flux. So here comes my problem: if I apply models which does not add viscosity in the wall regions (like WALE, Dynamic Smagorinsky, the Sigma-model) the flux increases and the mean velocity profiles becomes worse than the ones obtained with underresolved DNS! The code is identical, the implementations of the LES models are 100% correct, they have been tested for a more "physical" case resulting in good mean profiles. I have checked the contribution of 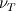 for these models; it is positive, and of the same magnitude as for the Smagorinsky model, the only difference is that no eddy-viscosity is added in wall regions. for these models; it is positive, and of the same magnitude as for the Smagorinsky model, the only difference is that no eddy-viscosity is added in wall regions.My question is: is this behaviour explainable? Is it correct? Everything points to there being a problem for a selection of LES models for this special case. My problem is, I can't find an explanation on why this happens! I have implemented the solution of this problem where the mass-flux is controlled, that may work better than the constant pressure gradient equal to 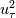 . .
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
I have some question:
- what about the discretization method? - why don't you fix the constant pressure gradient to -1 ? it directly provides the non-dimensional velocity in terms of v+, you do not need to correct any mass flux. - check your solution for a case running without any SGS model (LES no-model) - what about you energy spectra? it is not a new fact that some LES solutions give a velocity profiles not so close to DNS. You can see also here: http://www.academia.edu/3958690/A_co...mulation_codes |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Join Date: Nov 2014
Posts: 9
Rep Power: 11  |
- what about the discretization method?
Finite Element method, both P1P1 and P2P1 element pairs for velocity and pressure has been tested, same results achieved. Incremental Pressure Correction scheme, Crank-Nicolson in time. - why don't you fix the constant pressure gradient to -1 ? it directly provides the non-dimensional velocity in terms of v+, you do not need to correct any mass flux. That may be interesting to try, but how to control which turbulent Reynolds number the flow represents then? - check your solution for a case running without any SGS model (LES no-model) The solution with no LES model is good, the flux stabilizes at a higher flux than that of fully resolved DNS. It hence becomes natural to activate a LES model as it then is expected that the addition of eddy-viscosity will pull the mean velocities down towards the DNS data. - what about you energy spectra? Haven't checked anything here. And thanks for the link to the paper, I'll check it out! |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
When the constant pressure gradient is fixed to -1, the non-dimensional momentum equations show directly the molecular diffusive coefficient as (1/Re_tau). Therefore, that is the input value of your case.
|
|
|
|

|
|
|
|
|
#5 |
|
New Member
Join Date: Nov 2014
Posts: 9
Rep Power: 11  |
Thanks for the tip FMDenaro, I will give it a shot.
Here is a plot just to give you an illustration of what happens:  As you can see the Smagorinsky model really kicks in, whereas the Wale model results in a higher mean velocity profile. It's quite counter intuitive behaviour. But from your article FMDenaro it is clear that this also happens for the Dynamic Smagorinsky model for some codes (TransAT, Code Saturne and your own FV-Based code)... |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
Smagorinsky_016 is clearly wrong
|
|
|
|

|
|
|
|
|
#7 |
|
New Member
Join Date: Nov 2014
Posts: 9
Rep Power: 11  |
Is it wrong as in that the model in general is a bad and very over-dissipative model? It's the traditional Smagorinsky model, not the Dynamic one. The Dynamic model gives results similar to Wale.
|
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
It's wrong in the viscous sub-layer...do You use a dumping function?
|
|
|
|

|
|
|
|
|
#9 |
|
New Member
Join Date: Nov 2014
Posts: 9
Rep Power: 11  |
No, the traditional Smagorinsky model is for testing only, hence no wall functions :-)
|
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,813
Rep Power: 73    |
No, i am talking about the dumping function not the wall model
|
|
|
|

|
|
|
|
|
#11 |
|
New Member
Join Date: Nov 2014
Posts: 9
Rep Power: 11  |
You mean damping functions like Van Driest? If yes, as mentioned the Smagorinsky model is just for testing only such that its cons are illustrated.
|
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,704
Rep Power: 66    |
The Smagorinsky model gives non-zero eddy viscosity near boundaries. So yes it's overly dissipative in the near-wall region. If you want to highlight cons then surely this is a big con of the Smagorinsky model w/o damping functions. No surprise that you get weird results. I think you need to include the Van Driest damping near the wall to make any sense of the LES results.
|
|
|
|

|
|
|
|
|
#13 |
|
New Member
Join Date: Nov 2014
Posts: 9
Rep Power: 11  |
Thanks for your reply, LuckyTran!
So, I am happy with the results from the Smagorinsky model without damping functions since the results obtained are "correct" and as expected. The problem lies in the Wale model; as you see from the plot activating this model results in higher mean velocity compared to underresolved DNS. It's quite opposite of what is expected. The same thing happens for the Sigma-model, and the Dynamic Smagorinsky model; mean velocity increases. I have checked the code and everything is correct, as mentioned all models work very well for a different test case. Hence everything points to something happening for this specific simulation when LES models that do not add eddy-viscosity in the wall regions are applied. |
|
|
|

|
|
|
|
|
#14 |
|
Senior Member
|
I already met this behavior. You might want to check out my thesis here:
http://www.cfd-online.com/Forums/blo...hesis-les.html At page 173 you will find a comparison of several SGS models on the channel flow. A tentative explanation is given. We (LESinItaly) also had a tentative paper on this, but time was our enemy. Some of us are trying to recap this thing in a new paper, but time is still not going to help (as we all do different jobs now). Roughly speaking: the optimal near wall behavior of a SGS model is not uniquely defined (y^3) but is going to depend on your numerical method. It turns out that instead of the y^3 (which is practically a null contribution), you might need something like y^2 or even y, so that the SGS model can counteract the fact that your numerical method is unable to reconstruct the u'v' fluctuations near the wall. That is, what is good for a spectral method (y^3) might not be for a 2nd order code. |
|
|
|

|
|
|
|
|
#15 |
|
New Member
Join Date: Nov 2014
Posts: 9
Rep Power: 11  |
Thank you for an excellent answer, sbaffini! So it can be explained, that is just what I was hoping for. I'll check out your thesis, looks very interesting!
My code is 2nd order in both time and space, hence as you say reproduction of u'v' fluctuations is problematic. I get the same results as you do for my Dynamic Smagorinsky and Sigma-model, so that's nice. |
|
|
|

|
|
 |
| Tags |
| channel flow, dns, les, smagorinsky, wale |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| LES of turbulent channel flows | cedric_duprat | OpenFOAM Running, Solving & CFD | 220 | November 18, 2019 04:19 |
| About Some Concepts:Laminar flow, turbulent flow, steady flow and time-dependent flow | Jing | Main CFD Forum | 8 | October 5, 2018 17:02 |
| Channel flow with heat flux | Cara Gao | OpenFOAM Pre-Processing | 4 | September 28, 2014 18:52 |
| Serious problems to perform LES of the channel flow | LB76 | OpenFOAM Verification & Validation | 5 | June 21, 2012 07:40 |
| LES of a turbulent channel flow stays laminar | liu | OpenFOAM Running, Solving & CFD | 2 | May 27, 2010 13:53 |