Closing on wall functions - part 7: starting from a profile
It might happens that one doesn't have a turbulent viscosity profile but actually has just an equilibrium profile for velocity or temperature. More specifically:
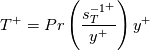
with its obvious extension to the velocity case. In order to go back to the framework presented here one should notice that:
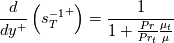
from which, it follows that:
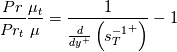
which is all that is needed to compute (numerically if not doable analytically) the remaining integrals for non equilibrium and/or TKE production terms.
For the non equilibrium terms this leads to the following:
![{s_T^i}^+ = \int_0^{y+}{\frac{z^{i+1}}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz} = \int_0^{y+}z^{i+1}\frac{d}{dz}\left({s_T^{-1}}^+\right)dz {s_T^i}^+ = \int_0^{y+}{\frac{z^{i+1}}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz} = \int_0^{y+}z^{i+1}\frac{d}{dz}\left({s_T^{-1}}^+\right)dz](/Forums/vbLatex/img/24c695ea6dfc3137676d388d28b45f8c-1.gif)
Hence, integration by parts finally leads to:
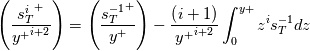
Formally, this is the generalized trick that I used here to extend the Reichardt wall law to constant only non equilibrium cases (i.e., i=0).
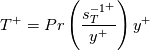
with its obvious extension to the velocity case. In order to go back to the framework presented here one should notice that:
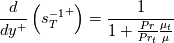
from which, it follows that:
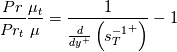
which is all that is needed to compute (numerically if not doable analytically) the remaining integrals for non equilibrium and/or TKE production terms.
For the non equilibrium terms this leads to the following:
![{s_T^i}^+ = \int_0^{y+}{\frac{z^{i+1}}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz} = \int_0^{y+}z^{i+1}\frac{d}{dz}\left({s_T^{-1}}^+\right)dz {s_T^i}^+ = \int_0^{y+}{\frac{z^{i+1}}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz} = \int_0^{y+}z^{i+1}\frac{d}{dz}\left({s_T^{-1}}^+\right)dz](/Forums/vbLatex/img/24c695ea6dfc3137676d388d28b45f8c-1.gif)
Hence, integration by parts finally leads to:
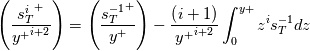
Formally, this is the generalized trick that I used here to extend the Reichardt wall law to constant only non equilibrium cases (i.e., i=0).
Total Comments 0





