Closing on wall functions - part 6: viscous dissipation
One thing which is missing in the previous derivations is the viscous dissipation term in the temperature equation. Let's reconsider the initial temperature equation when it is present:
![\frac{d}{dy}\left[C_p\left(\frac{\mu}{Pr}+\frac{\mu_t}{Pr_t}\right)\frac{dT}{dy}\right]=F_T - \frac{d}{dy}\left[\left(\mu+\mu_t\right)U\frac{dU}{dy}\right]](/Forums/vbLatex/img/a4cb00b946f9e49c483e638f60b5b8b5-1.gif "\frac{d}{dy}\left[C_p\left(\frac{\mu}{Pr}+\frac{\mu_t}{Pr_t}\right)\frac{dT}{dy}\right]=F_T - \frac{d}{dy}\left[\left(\mu+\mu_t\right)U\frac{dU}{dy}\right]")
A first integration leads to:
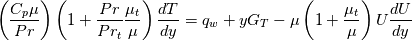
where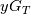
is the integral of 
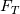and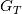 
has the same form we assumed for 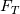, just with its coefficients divided by 
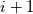. Then a further integration leads to:
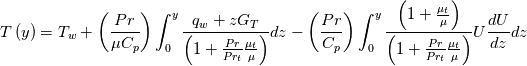
The first integral in the equation above has been the subject of the previous posts, while the neglected viscous dissipation term is the last term in the equation. Now, there are two ways which could be used to proceed. A first one involves invoking the velocity equation and transforming the viscous dissipation term as follows:
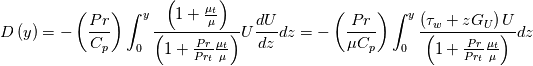
where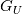
has the same form as 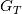, but with the velocity coefficients. At this point, then, one can note that the integral has the exact same form of the first one, but with the additional velocity 
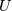in it. I have not attempted to solve it with none of the models presented but, even if doable, I expect high levels of cumbersomeness.
One could approximate the integral by assuming a constant, representative, value for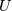, say, 
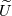and take it out of the integral. In this case, while one should still be careful in mixing the velocity numerator with the temperature denominator in the integrand, the resulting integral would be formally identical to the first one, which we have solved in previous posts.
A second, preferred way to proceed would instead first recognize that the integral above can be transformed as:
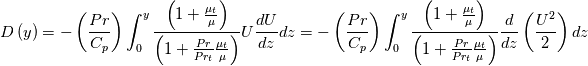
Hence integration by parts leads to the following result:
![D\left(y\right)=-\left(\frac{Pr}{2C_p}\right)\left\{U^2\frac{\left(1+\frac{\mu_t}{\mu}\right)}{\left(1+\frac{Pr}{Pr_t}\frac{\mu_t}{\mu}\right)}-U_w^2-\int_{0}^{y}U^2\frac{d}{dz}\left[\frac{\left(1+\frac{\mu_t}{\mu}\right)}{\left(1+\frac{Pr}{Pr_t}\frac{\mu_t}{\mu}\right)}\right]dz\right\}](/Forums/vbLatex/img/64dc52784fae5d5c7e75f5835fa9ae79-1.gif "D\left(y\right)=-\left(\frac{Pr}{2C_p}\right)\left\{U^2\frac{\left(1+\frac{\mu_t}{\mu}\right)}{\left(1+\frac{Pr}{Pr_t}\frac{\mu_t}{\mu}\right)}-U_w^2-\int_{0}^{y}U^2\frac{d}{dz}\left[\frac{\left(1+\frac{\mu_t}{\mu}\right)}{\left(1+\frac{Pr}{Pr_t}\frac{\mu_t}{\mu}\right)}\right]dz\right\}")
At this point we are still left with an even more cumbersome integral to evaluate, if possible at all. However, this integral is exactly 0 in two special cases: fully laminar ones (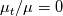
) and when 
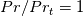. Another advanatge of this form is that if we now assume a constant, representative, value for 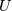, say, 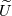and take it out of the integral, we are left with no more work to do and just obtain:
![D\left(y\right)=-\left(\frac{Pr}{2C_p}\right)\left[\left(U^2-\widetilde{U}^2\right)\frac{\left(1+\frac{\mu_t}{\mu}\right)}{\left(1+\frac{Pr}{Pr_t}\frac{\mu_t}{\mu}\right)}-\left(U_w^2-\widetilde{U}^2\right)\right]](/Forums/vbLatex/img/a8b83e5526d549404175d5556a02f652-1.gif "D\left(y\right)=-\left(\frac{Pr}{2C_p}\right)\left[\left(U^2-\widetilde{U}^2\right)\frac{\left(1+\frac{\mu_t}{\mu}\right)}{\left(1+\frac{Pr}{Pr_t}\frac{\mu_t}{\mu}\right)}-\left(U_w^2-\widetilde{U}^2\right)\right]")
which also always works in the cases where the integral is exactly 0. Of course, we are now left with determining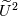
, but this seems a more reasonable task, also because it must be representative just for the region where derivative in the integrand is not 0 and not the full y length. A value for 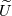commonly used with standard wall functions is the velocity at 
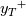. By extension, for the Musker-Monkewitz wall function one could use the velocity at 
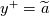, the profile constant modified by the 
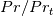ratio (see here). In more general cases, it seems that a good generalization for 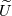is the velocity at the point where 
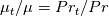, which is where the term under the derivative reaches half its maximum excursion.
However, this whole presentation is an approximate solution to the original problem for the viscous dissipation, that's why I left it out of the general discussion of the previous posts.
A first integration leads to:
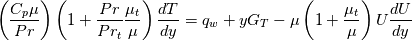
where
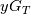is the integral of 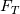and 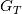has the same form we assumed for 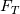, just with its coefficients divided by 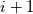. Then a further integration leads to: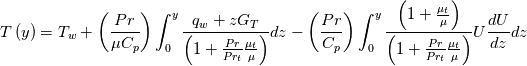The first integral in the equation above has been the subject of the previous posts, while the neglected viscous dissipation term is the last term in the equation. Now, there are two ways which could be used to proceed. A first one involves invoking the velocity equation and transforming the viscous dissipation term as follows:
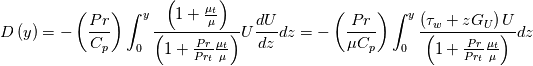
where
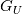has the same form as 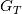, but with the velocity coefficients. At this point, then, one can note that the integral has the exact same form of the first one, but with the additional velocity 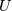in it. I have not attempted to solve it with none of the models presented but, even if doable, I expect high levels of cumbersomeness.One could approximate the integral by assuming a constant, representative, value for
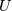, say, 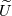and take it out of the integral. In this case, while one should still be careful in mixing the velocity numerator with the temperature denominator in the integrand, the resulting integral would be formally identical to the first one, which we have solved in previous posts.A second, preferred way to proceed would instead first recognize that the integral above can be transformed as:
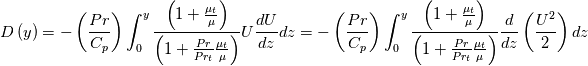
Hence integration by parts leads to the following result:
At this point we are still left with an even more cumbersome integral to evaluate, if possible at all. However, this integral is exactly 0 in two special cases: fully laminar ones (
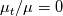) and when 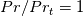. Another advanatge of this form is that if we now assume a constant, representative, value for 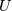, say, 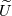and take it out of the integral, we are left with no more work to do and just obtain:which also always works in the cases where the integral is exactly 0. Of course, we are now left with determining
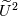, but this seems a more reasonable task, also because it must be representative just for the region where derivative in the integrand is not 0 and not the full y length. A value for 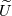commonly used with standard wall functions is the velocity at 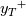. By extension, for the Musker-Monkewitz wall function one could use the velocity at 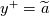, the profile constant modified by the 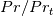ratio (see here). In more general cases, it seems that a good generalization for 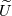is the velocity at the point where 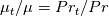, which is where the term under the derivative reaches half its maximum excursion.However, this whole presentation is an approximate solution to the original problem for the viscous dissipation, that's why I left it out of the general discussion of the previous posts.
Total Comments 0
