2 Easy MPI pieces
Anyone who has a minimum working experience with MPI (the Message Passing Interface for distributed parallel computing) has certainly had the chance to meet certain coding patterns multiple times, especially if working with a CFD (or any other computational physics like) code.
Regrettably, MPI and parallel distributed computing is one of those areas where textbooks and online examples (even SO) are largely useless, as most (if not all) of them just simply go into the details of how to use this or that feature. But most examples are so toy level that you even find cases where the presented code just works for a fixed number of processes (aaargh!).
Every MPI use case is very specific but, I want to present here two examples that are so simple and stupid that it is a shame they are not present in every single book or tutorial. Yet, they have both very practical use cases.
The first MPI piece I want to present is, superficially, related to the necessity to perform a deadlock avoiding loop among all processes. This problem, however, really is a twofold one. On one side, the main issue is: how do I automatically schedule the communications between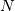 processes so that, for any couple of processes
processes so that, for any couple of processes  and
and  , if the
, if the 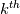 communication partner of process
communication partner of process  is process
is process  then the
then the 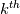 communication partner of process
communication partner of process  is process
is process  ? With a proper communication schedule in place, avoiding deadlock, which is the second part of the problem, is then definitely a triviality (also present in most MPI examples). It turns out that such communication schedule is a triviality as well, to the point of being a single liner solution, so it really is a shame that it is not presented anywhere (to the best of my knowledge). So, here it is a pseudocode example of a loop where each process communicates with each other process (including itself) without deadlock (full Fortran example here):
? With a proper communication schedule in place, avoiding deadlock, which is the second part of the problem, is then definitely a triviality (also present in most MPI examples). It turns out that such communication schedule is a triviality as well, to the point of being a single liner solution, so it really is a shame that it is not presented anywhere (to the best of my knowledge). So, here it is a pseudocode example of a loop where each process communicates with each other process (including itself) without deadlock (full Fortran example here):
where the modulo operation is intended as the Fortran one. All the magic here happens in the determination of myp, the communication partner for the given process at the i-th stage, which is different for each process at each stage, but exactly match between them at any given stage.
Now, the pseudo-code above (and the one in the linked gist as well) is just an example, and you should not, DEFINITELY, do this sort of loops in your code. Also, you should not use blocking sends and recvs as well (I used them in the example to prove its very point). However, even for non blocking send/recv, and even when each process just has to communicate with a limited set of different processes, it turns out that this schedule is extremely efficient, as very little to none is spent in the handling of non matched send/recv calls. Now, for how stupid and simple this might look, most codes, even large scale ones, simply don't schedule their communications, which is the reason I thought to share this simple piece of code. In practice I have several variants of it (I provided 2 of them in the linked gist) as today I use it to schedule different pieces of communications in my code.
The second easy MPI piece is related to a very simple case: how would you write your own reduce operation without using mpi_reduce but just mpi_send/recv? While this might just look like a textbook exercise, it is indeed relevant for those cases where the needed reduce operation is not among the intrinsic ones of MPI (SUM, MAX, etc.). I first had a need for it when working on parallel statistics (e.g., how to compute the spatial statistics of a field variable in a finite volume code without using allreduce, which costs just like an mpi_barrier?).
For the most complex cases, MPI provides both an mpi_type_create_struct routine to create a generic user-defined data type and mpi_op_create routine to define a custom reduction operation for said data type (see, for example, here, here and here). Unfortunately, they can't actually cover all use cases, or at least not so straightforwardly.
However, if there are no specific needs in terms of the associativity of the reduce operator, it turns out that you can write your own reduce algorithm with no more than 25 lines of code (full Fortran example here). The algorithm has 3 very simple steps:
The final reduce operation will then be available to the process with rank 0 (which could simply send it to the required root, if different). Note that the algorithm still needs nproc-1 messages to be sent/received but, differently from the naive case where a root process directly receives all the messages one after the other, here the messages of each stage are always between different couples of processes. Of course, by using such simple approach you abandon the possibility to use any possible optimizations on the MPI side (which, however, might not be available at all for the user defined data type and operator), but there is a very large gain in flexibility and simplicity.
If there are associativity needs, you can instead follow this Fortran example, where the MPICH binomial tree algorithm is used. The algorithm (which is shorter and largely more elegant, yet a bit dense in its logic) performs the reduction by following the rank order of the processes, so it is very easy to map them in order to follow a more specific order.
Regrettably, MPI and parallel distributed computing is one of those areas where textbooks and online examples (even SO) are largely useless, as most (if not all) of them just simply go into the details of how to use this or that feature. But most examples are so toy level that you even find cases where the presented code just works for a fixed number of processes (aaargh!).
Every MPI use case is very specific but, I want to present here two examples that are so simple and stupid that it is a shame they are not present in every single book or tutorial. Yet, they have both very practical use cases.
The first MPI piece I want to present is, superficially, related to the necessity to perform a deadlock avoiding loop among all processes. This problem, however, really is a twofold one. On one side, the main issue is: how do I automatically schedule the communications between
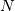 processes so that, for any couple of processes
processes so that, for any couple of processes  and
and  , if the
, if the 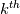 communication partner of process
communication partner of process  is process
is process  then the
then the 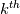 communication partner of process
communication partner of process  is process
is process  ? With a proper communication schedule in place, avoiding deadlock, which is the second part of the problem, is then definitely a triviality (also present in most MPI examples). It turns out that such communication schedule is a triviality as well, to the point of being a single liner solution, so it really is a shame that it is not presented anywhere (to the best of my knowledge). So, here it is a pseudocode example of a loop where each process communicates with each other process (including itself) without deadlock (full Fortran example here):
? With a proper communication schedule in place, avoiding deadlock, which is the second part of the problem, is then definitely a triviality (also present in most MPI examples). It turns out that such communication schedule is a triviality as well, to the point of being a single liner solution, so it really is a shame that it is not presented anywhere (to the best of my knowledge). So, here it is a pseudocode example of a loop where each process communicates with each other process (including itself) without deadlock (full Fortran example here):Code:
nproc = mpi_comm_size !How many processes
myid = mpi_comm_rank !My rank among processes
!Loop over all processes
for i = 1 : nprocs
!My communication partner at the i-th stage
myp = modulo(i-myid-1,nproc)
if (myid>myp) then
!The process with higher rank sends and then receives
mpi_send
mpi_recv
elseif (myid<myp) then
!The process with lower rank receives and then sends
mpi_recv
mpi_send
else
!This is me, no send or recv actually needed
endif
endfor
Now, the pseudo-code above (and the one in the linked gist as well) is just an example, and you should not, DEFINITELY, do this sort of loops in your code. Also, you should not use blocking sends and recvs as well (I used them in the example to prove its very point). However, even for non blocking send/recv, and even when each process just has to communicate with a limited set of different processes, it turns out that this schedule is extremely efficient, as very little to none is spent in the handling of non matched send/recv calls. Now, for how stupid and simple this might look, most codes, even large scale ones, simply don't schedule their communications, which is the reason I thought to share this simple piece of code. In practice I have several variants of it (I provided 2 of them in the linked gist) as today I use it to schedule different pieces of communications in my code.
The second easy MPI piece is related to a very simple case: how would you write your own reduce operation without using mpi_reduce but just mpi_send/recv? While this might just look like a textbook exercise, it is indeed relevant for those cases where the needed reduce operation is not among the intrinsic ones of MPI (SUM, MAX, etc.). I first had a need for it when working on parallel statistics (e.g., how to compute the spatial statistics of a field variable in a finite volume code without using allreduce, which costs just like an mpi_barrier?).
For the most complex cases, MPI provides both an mpi_type_create_struct routine to create a generic user-defined data type and mpi_op_create routine to define a custom reduction operation for said data type (see, for example, here, here and here). Unfortunately, they can't actually cover all use cases, or at least not so straightforwardly.
However, if there are no specific needs in terms of the associativity of the reduce operator, it turns out that you can write your own reduce algorithm with no more than 25 lines of code (full Fortran example here). The algorithm has 3 very simple steps:
- Determine pp2, the largest power of 2 integer smaller than or equal to the current number of processes
- If the current number of processes is above pp2, ranks beyond pp2 just send their data to ranks that are lower by exactly pp2 (e.g., for 7 processes, zero indexed, ranks from 4 to 6 will send, respectively, to ranks from 0 to 2), which will perform the reduce operation
- Log2(pp2) iterations are performed where, at each iteration, the higher half of ranks up to a given power of 2, ppd (=pp2 at the beginning of the first iteration), send their data to the lower half (shifting by ppd/2), which will then reduce it. At the end of each iteration ppd is divided by 2.
The final reduce operation will then be available to the process with rank 0 (which could simply send it to the required root, if different). Note that the algorithm still needs nproc-1 messages to be sent/received but, differently from the naive case where a root process directly receives all the messages one after the other, here the messages of each stage are always between different couples of processes. Of course, by using such simple approach you abandon the possibility to use any possible optimizations on the MPI side (which, however, might not be available at all for the user defined data type and operator), but there is a very large gain in flexibility and simplicity.
If there are associativity needs, you can instead follow this Fortran example, where the MPICH binomial tree algorithm is used. The algorithm (which is shorter and largely more elegant, yet a bit dense in its logic) performs the reduction by following the rank order of the processes, so it is very easy to map them in order to follow a more specific order.
Total Comments 0





