Basic Fluid Mechanics and CFD Anything related to the general theory of fluid flows and their computation
|
|||
|
Posted in Basic Fluid Mechanics and CFD
Views 1566
Comments 0

|
|
|||
|
Posted in Basic Fluid Mechanics and CFD
Views 1641
Comments 0

|
|
|||
|
Posted in Basic Fluid Mechanics and CFD
Views 2246
Comments 0

|
|
|||
|
Posted in Basic Fluid Mechanics and CFD
Views 4790
Comments 0

|
|
|||
|
Posted in Basic Fluid Mechanics and CFD
Views 2679
Comments 2

|

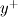

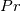
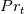
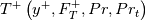
![\frac{dT^+}{dy^+}=\frac{Pr\left(1+F_T^+y^+\right)}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]} \frac{dT^+}{dy^+}=\frac{Pr\left(1+F_T^+y^+\right)}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}](/Forums/vbLatex/img/6f93b3151b1a95e271960766dd7c8d1d-1.gif)
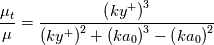

![f^+\left(y^+,\frac{Pr}{Pr_t}\right)=\int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+} f^+\left(y^+,\frac{Pr}{Pr_t}\right)=\int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}](/Forums/vbLatex/img/3cf5c7f8d4135bc15c2210e0f07028d5-1.gif)