Closing on wall functions - part 5: testing scripts
I provide here a set of MATLAB scripts to test all the claims made in the first 4 parts.
The first group of scripts is actually made of functions, that you are not supposed to directly call or modify:
The second group of scripts is the one actually making the tests and the comparisons:
Few comments on the use of the scripts above and some claims made in previous posts.
In the second post of this series I mentioned that, when using the Spalart-Allmaras model, one could avoid iterations to find by using
by using 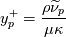 . This is confirmed in check.m where the Spalart-Allmaras boundary conditions for the solution of the 1D ODE are obtained from the relation above using as input the
. This is confirmed in check.m where the Spalart-Allmaras boundary conditions for the solution of the 1D ODE are obtained from the relation above using as input the 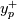 value obtained by the underlying wall function.
value obtained by the underlying wall function.
In the same post it is also mentioned that one could precompute the wall function for a given range of parameters and later interpolate from it. Such precomputation is what the script wfmap.m does, and you can also see from the commented parts how it could be adapted to directly use the 1D ODE solution instead of the musker profile actually used by the script.
Still in the same post, I mentioned how, for non equilibrium cases, the iterative computation of might become cumbersome as multiple solution branches might exist for non favourable pressure gradients. This can be easily visualized by using wfiter.m.
might become cumbersome as multiple solution branches might exist for non favourable pressure gradients. This can be easily visualized by using wfiter.m.
It has been mentioned here that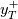 in the standard profile can be obtained by few iterations of the Halley's method. The specific implementation is in iteryv.m.
in the standard profile can be obtained by few iterations of the Halley's method. The specific implementation is in iteryv.m.
In the last post I have mentioned that the van Driest damped mixing length is, indeed, mostly equivalent to the Musker profile for the incompressible formulation used here. This is clearly shown in wfcompare.m. While I don't directly provide the 1D ODE solution with the mixing length (just its wall function form trough numericalsp), I do for two different turbulent viscosity formulations trough the Spalart-Allmaras model in check.m and show that they correspond to the analogous formulation used as wall function.
All the scripts are in a zipped folder for convenience (as a maximum of 5 files can be uploaded here) and have been tested with MATLAB R2022a.
The first group of scripts is actually made of functions, that you are not supposed to directly call or modify:
- muskersp.m: returns
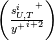 ,
, 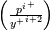 and
and 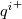 as shown here. It only works for N up to 0 (constant non equilibrium terms) EDIT: There is an apparently innocuous mistake in the limiting behavior of s, as it should not use the factor prprt for the thermal case. It seems innocuous as it only affects the first order term, which probably is already negligible, and only for the temperature case (so in the scripts it is only used for plotting purposes, and probably never at those low
as shown here. It only works for N up to 0 (constant non equilibrium terms) EDIT: There is an apparently innocuous mistake in the limiting behavior of s, as it should not use the factor prprt for the thermal case. It seems innocuous as it only affects the first order term, which probably is already negligible, and only for the temperature case (so in the scripts it is only used for plotting purposes, and probably never at those low 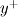 ).
). - standardsp.m: returns the same quantities but for the standard wall function presented here. It works for arbitrary N but the scripts below only test it up to 0 (constant non equilibrium terms)
- iteryv.m: returns the value of
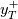 needed by standardsp.m for
needed by standardsp.m for 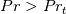
- numericalsp.m: a generic wall function that takes as input a function handle for the turbulent viscosity ratio and provides the required integrals by numerical integration. It works for arbitrary N (but, again, it is only tested for N up to 0). It only works for turbulent viscosities going to 0 at least as fast as
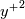 .
. - standard.m: the actual standard wall function adapted to the present framework for comparisons. Only works for equilibrium cases (N=-1)
- spiter.m: the function that performs the iterations on the wall functions to find
 following what is presented here
following what is presented here - sa1d.m: solves the original ODE of the problem (actually a slightly more general one) using a second order cell centered finite volume discretization, the Spalart-Allmaras turbulence model (actually a generalized version that also works with the Musker profile) and the tridiagonal solver
The second group of scripts is the one actually making the tests and the comparisons:
- check.m: for given flow conditions, it tests that a) the analytical musker profile in muskersp is consistent with the one obtained trough numerical integration with numericalsp, b) that the numerical musker profile (and, by point a above, also the analytical one) is consistent with the Spalart-Allmaras direct solution of the ODE with a properly modified fv1 function c) that the numericalsp routine (already tested in a and b above) is consistent with the non modified Spalart-Allmaras solution of the ODE when the relative turbulent viscosity profile is used. Note that the velocity wall function can only match the Spalart-Allmaras solution in the equilibrium case (dpdx=0), but in the same case the temperature equation can have non equilibrium terms and the solutions will match.
- wfiter.m: for a given wall function (user selectable) and flow conditions plots the iterations to find
 as produced by itersp.m
as produced by itersp.m - wfcompare.m: a straightforward comparison of multiple wall functions for given flow conditions
- wfmap.m: for the musker profile (but easily adaptable to other profiles) it maps the solution
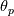 of the iterative procedure to find
of the iterative procedure to find  in a certain range of
in a certain range of 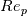 and
and  parameters.
parameters. - apr.m: a comparison of the variations of the constant
 in the Musker profile and
in the Musker profile and 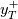 in the standard profile as a function of
in the standard profile as a function of 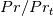 giving a sensation of how the variation of the Musker constant with
giving a sensation of how the variation of the Musker constant with 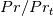 is, indeed, a sort of Jayatilleke term.
is, indeed, a sort of Jayatilleke term.
Few comments on the use of the scripts above and some claims made in previous posts.
In the second post of this series I mentioned that, when using the Spalart-Allmaras model, one could avoid iterations to find
 by using
by using 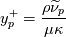 . This is confirmed in check.m where the Spalart-Allmaras boundary conditions for the solution of the 1D ODE are obtained from the relation above using as input the
. This is confirmed in check.m where the Spalart-Allmaras boundary conditions for the solution of the 1D ODE are obtained from the relation above using as input the 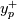 value obtained by the underlying wall function.
value obtained by the underlying wall function.In the same post it is also mentioned that one could precompute the wall function for a given range of parameters and later interpolate from it. Such precomputation is what the script wfmap.m does, and you can also see from the commented parts how it could be adapted to directly use the 1D ODE solution instead of the musker profile actually used by the script.
Still in the same post, I mentioned how, for non equilibrium cases, the iterative computation of
 might become cumbersome as multiple solution branches might exist for non favourable pressure gradients. This can be easily visualized by using wfiter.m.
might become cumbersome as multiple solution branches might exist for non favourable pressure gradients. This can be easily visualized by using wfiter.m.It has been mentioned here that
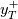 in the standard profile can be obtained by few iterations of the Halley's method. The specific implementation is in iteryv.m.
in the standard profile can be obtained by few iterations of the Halley's method. The specific implementation is in iteryv.m.In the last post I have mentioned that the van Driest damped mixing length is, indeed, mostly equivalent to the Musker profile for the incompressible formulation used here. This is clearly shown in wfcompare.m. While I don't directly provide the 1D ODE solution with the mixing length (just its wall function form trough numericalsp), I do for two different turbulent viscosity formulations trough the Spalart-Allmaras model in check.m and show that they correspond to the analogous formulation used as wall function.
All the scripts are in a zipped folder for convenience (as a maximum of 5 files can be uploaded here) and have been tested with MATLAB R2022a.
Total Comments 0





