A generalized thermal/dynamic wall function: Part 1
In a previous post i wrote about an extension of the Reichardt law of the wall to pressure gradient effects. That was derived by assuming the Reichardt profile as a solution for the case without pressure gradient and using integration by parts. In particular, given the the Reichardt function (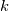 is the Von Karman constant):
is the Von Karman constant):
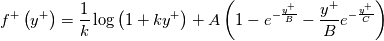
with:
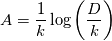
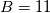

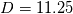
the pressure gradient sensitized formula for the velocity is given by:
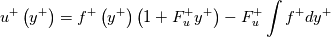
where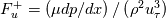 is the nondimensional pressure gradient.
is the nondimensional pressure gradient.
However, while useful for its purpose, this formulation turns out to have at least two drawbacks, both of which depending, somehow, on the fact that Reichardt didn't actually solved the underlying problem exactly. The first one is that the base profile (i.e., even without the pressure gradient effect) does not even reproduce the correct profile derivatives at the wall. Hence, as a main consequence, the formula might not be suitable as toy model for certain theoretical purposes. The second drawback, which is also another consequence of the same fact, is that it can be used as thermal wall function only for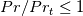 , as higher values will tend to amplify the part of the profile which is uncorrect.
, as higher values will tend to amplify the part of the profile which is uncorrect.
To overcome such issues, i follow here the same steps as before but with a different formulation for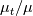 , using one which can be integrated exactly. We start from the temperature equation, which is more general:
, using one which can be integrated exactly. We start from the temperature equation, which is more general:
![\frac{d}{dy}\left[C_p\left(\frac{\mu}{Pr}+\frac{\mu_t}{Pr_t}\right)\frac{dT}{dy}\right]=F_T \frac{d}{dy}\left[C_p\left(\frac{\mu}{Pr}+\frac{\mu_t}{Pr_t}\right)\frac{dT}{dy}\right]=F_T](/Forums/vbLatex/img/0a6ecf7d1a227b166f5e9fa4142c0df0-1.gif)
where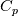 (constant pressure specific heat),
(constant pressure specific heat), 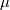 (dynamic viscosity),
(dynamic viscosity), 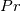 (Prandtl number),
(Prandtl number), 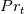 (turbulent Prandtl number) and
(turbulent Prandtl number) and 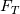 (defined in the following) are all constant. The fact that this equation correctly represents a large set of velocity/temperature viscous boundary conditions should be self-evident. For example,
(defined in the following) are all constant. The fact that this equation correctly represents a large set of velocity/temperature viscous boundary conditions should be self-evident. For example, 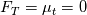 gives the classical linear relationship for the temperature (which becomes the one for the velocity when
gives the classical linear relationship for the temperature (which becomes the one for the velocity when 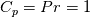 ). Also,
). Also, 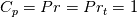 with
with 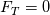 leads to the classical wall-function formulation (for certain forms of
leads to the classical wall-function formulation (for certain forms of 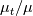 ). According to the specific equation form,
). According to the specific equation form, 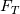 can have different meanings. For example, in the case of the velocity, it can include the wall-parallel pressure gradient (note that y is assumed to be the wall-normal coordinate, x the wall parallel one), the buoyancy term, etc. In general, it can include any of the terms that have been neglected in the LHS for the given equation. The only assumption here is that they are assumed constant along y (as will be shown in the following, it turns out that this can be actually relaxed).
can have different meanings. For example, in the case of the velocity, it can include the wall-parallel pressure gradient (note that y is assumed to be the wall-normal coordinate, x the wall parallel one), the buoyancy term, etc. In general, it can include any of the terms that have been neglected in the LHS for the given equation. The only assumption here is that they are assumed constant along y (as will be shown in the following, it turns out that this can be actually relaxed).
The first step to proceed is integrating the equation above once. This produces (using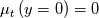 ):
):
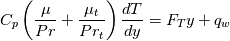
where (the
(the 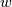 underscore meaning that it is evaluated at the wall, i.e., for
underscore meaning that it is evaluated at the wall, i.e., for 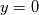 ). Multiplying by
). Multiplying by 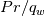 and rearranging, we obtain:
and rearranging, we obtain:
![\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]\frac{dT^+}{dy^+}=Pr\left(1+F_T^+y^+\right) \left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]\frac{dT^+}{dy^+}=Pr\left(1+F_T^+y^+\right)](/Forums/vbLatex/img/ec0a7c6b314f4985a4a3a82352ec320a-1.gif)
where:
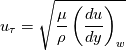
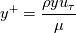
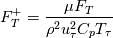

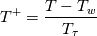
The same equation, interpreted for the velocity, would read:
![\left[1+\left(\frac{\mu_t}{\mu}\right)\right]\frac{du^+}{dy^+}=1+F_u^+y^+ \left[1+\left(\frac{\mu_t}{\mu}\right)\right]\frac{du^+}{dy^+}=1+F_u^+y^+](/Forums/vbLatex/img/57d73cd8f878e13b4d81fb3f811f02b8-1.gif)
where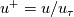 . This confirms that the temperature solution can also be used for the velocity by a proper interpretation of the terms. Going back to the temperature equation, we then end up with the following equation for the nondimensional temperature derivative:
. This confirms that the temperature solution can also be used for the velocity by a proper interpretation of the terms. Going back to the temperature equation, we then end up with the following equation for the nondimensional temperature derivative:
![\frac{dT^+}{dy^+}=\frac{Pr\left(1+F_T^+y^+\right)}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]} \frac{dT^+}{dy^+}=\frac{Pr\left(1+F_T^+y^+\right)}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}](/Forums/vbLatex/img/6f93b3151b1a95e271960766dd7c8d1d-1.gif)
Then, by a further integration:
![T^+\left(y^+\right)=Pr \left\{\int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}+\int_0^{y+}{\frac{F_T^+z^+}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}\right\} T^+\left(y^+\right)=Pr \left\{\int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}+\int_0^{y+}{\frac{F_T^+z^+}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}\right\}](/Forums/vbLatex/img/43b30907ca252d9284af261112e8653c-1.gif)
Note that i temporarily suspended the hypothesis that is constant. Now, let us also assume that we know the first integral, that is:
is constant. Now, let us also assume that we know the first integral, that is:
![\int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}=f^+\left(y^+\right) \int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}=f^+\left(y^+\right)](/Forums/vbLatex/img/d6d88feb731c9f2583155cd1349c99c1-1.gif)
is a known function. Then, the solution becomes:
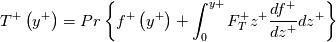
And after integration by parts:
![T^+\left(y^+\right)=Pr f^+\left(y^+\right)\left[1+F_T^+\left(y^+\right)y^+\right]-Pr\int_0^{y+}{f^+\left(F_T^++z^+\frac{dF_T^+}{dz^+}\right)dz^+} T^+\left(y^+\right)=Pr f^+\left(y^+\right)\left[1+F_T^+\left(y^+\right)y^+\right]-Pr\int_0^{y+}{f^+\left(F_T^++z^+\frac{dF_T^+}{dz^+}\right)dz^+}](/Forums/vbLatex/img/5ed4ad339bab706754cd2a99cb0c126e-1.gif)
For the sake of conciseness, let us also assume:
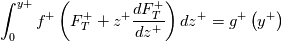
so that the full solution is:
![T^+\left(y^+\right)=Pr f^+\left(y^+\right)\left[1+F_T^+\left(y^+\right)y^+\right]-Pr g^+\left(y^+\right) T^+\left(y^+\right)=Pr f^+\left(y^+\right)\left[1+F_T^+\left(y^+\right)y^+\right]-Pr g^+\left(y^+\right)](/Forums/vbLatex/img/6ec7643a353ba9475910f82c1482acbf-1.gif)
While we have just moved the original problem to that of solving the two integrals for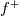 and
and 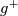 , those will actually turn out to be easier to solve. Note also that the parenthesis in
, those will actually turn out to be easier to solve. Note also that the parenthesis in 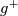 is a polynomial of the same order of
is a polynomial of the same order of  (assuming that it is approximated with a certain degree polynomial). Particularly relevant is the case with
(assuming that it is approximated with a certain degree polynomial). Particularly relevant is the case with  constant (as is typically assumed). However, note that ,for the
constant (as is typically assumed). However, note that ,for the 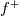 that we are going to derive below, a linear approximation is also integrable, as well as any other polynomial of higher degree. Obviously, things rapidly become cumbersome, with the degree of the polynomial, so for the present purposes it is sufficient to go back to the case
that we are going to derive below, a linear approximation is also integrable, as well as any other polynomial of higher degree. Obviously, things rapidly become cumbersome, with the degree of the polynomial, so for the present purposes it is sufficient to go back to the case  constant. In this case
constant. In this case 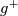 is simply the integral of
is simply the integral of 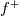 times
times  . Note that Popovac and Hanjalic have shown (for the velocity) that this is actually relevant for several practical cases. Nonetheless, is worth remembering that this is not a costriction of the present approach (probably it wasn't neither when
. Note that Popovac and Hanjalic have shown (for the velocity) that this is actually relevant for several practical cases. Nonetheless, is worth remembering that this is not a costriction of the present approach (probably it wasn't neither when 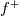 was based on the Reichardt profile).
was based on the Reichardt profile).
So, at this point we are left with determining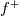 . To this end, we need a model for
. To this end, we need a model for 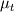 . Note that this is not different from the approach used by Van Driest to determine his velocity profile. It's just that the mixing length hypothesis he used led to a non integrable function. The same also happened to Reichardt, who then started modificating his function until something integrable came out.
. Note that this is not different from the approach used by Van Driest to determine his velocity profile. It's just that the mixing length hypothesis he used led to a non integrable function. The same also happened to Reichardt, who then started modificating his function until something integrable came out.
To overcome this limit, here we abandon those formulations and use instead the one from Musker:
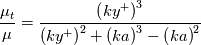
with being, in its original formulation, a constant (see below). It is worth mentioning that this functional form respects both the
being, in its original formulation, a constant (see below). It is worth mentioning that this functional form respects both the 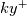 behavior for
behavior for 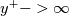 and the
and the 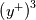 behavior for
behavior for  .
.
Note also that the Spalart-Allmaras model has a simlar behavior near the wall (see Allmaras et al., ICCFD 2012):
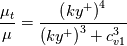
which then fails to recover the correct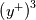 behavior for
behavior for  (However, Spalart and Allmaras explicitly mention in their original 1994 work that thay didn't notice any meaningful difference deriving from using this specific form instead of a correct one, say, the mixing length). This just to say that the Musker form is not only meaningful, but also representative of the near wall behavior of the Spalart-Allmaras model.
(However, Spalart and Allmaras explicitly mention in their original 1994 work that thay didn't notice any meaningful difference deriving from using this specific form instead of a correct one, say, the mixing length). This just to say that the Musker form is not only meaningful, but also representative of the near wall behavior of the Spalart-Allmaras model.
To solve for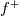 with the Musker turbulent viscosity, we first consider the case
with the Musker turbulent viscosity, we first consider the case 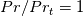 , as this already has a known solution, provided in its most general form by Monkewitz et al. (POF 20, 105102, 2008):
, as this already has a known solution, provided in its most general form by Monkewitz et al. (POF 20, 105102, 2008):
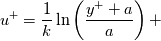
![\frac{\alpha}{a+4\alpha}\left\{\left(a-4\alpha\right)\ln\left[\frac{a\left[\left(y^+-\alpha\right)^2+\beta^2\right]}{2\alpha\left(y^++a\right)^2}\right]+\gamma\left[\arctan\left(\frac{y^+-\alpha}{\beta}\right)+\arctan\left(\frac{\alpha}{\beta}\right)\right]\right\} \frac{\alpha}{a+4\alpha}\left\{\left(a-4\alpha\right)\ln\left[\frac{a\left[\left(y^+-\alpha\right)^2+\beta^2\right]}{2\alpha\left(y^++a\right)^2}\right]+\gamma\left[\arctan\left(\frac{y^+-\alpha}{\beta}\right)+\arctan\left(\frac{\alpha}{\beta}\right)\right]\right\}](/Forums/vbLatex/img/555f1e220bd91848e372424c88a2ca07-1.gif)
where:
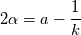
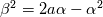
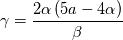
The constant is found by calibration with the turbulent velocity profile. Monkewitz et al. use
is found by calibration with the turbulent velocity profile. Monkewitz et al. use 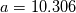 . In contrast, i calibrated the constant using the mixing length model with a constant
. In contrast, i calibrated the constant using the mixing length model with a constant 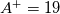 , resulting in
, resulting in 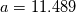 .
.
Now, the whole point of the procedure is: how to extend such formulation to the case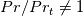 ? See part 2
? See part 2
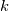 is the Von Karman constant):
is the Von Karman constant):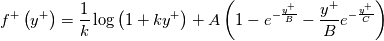
with:
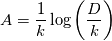
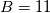

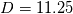
the pressure gradient sensitized formula for the velocity is given by:
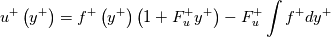
where
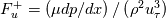 is the nondimensional pressure gradient.
is the nondimensional pressure gradient.However, while useful for its purpose, this formulation turns out to have at least two drawbacks, both of which depending, somehow, on the fact that Reichardt didn't actually solved the underlying problem exactly. The first one is that the base profile (i.e., even without the pressure gradient effect) does not even reproduce the correct profile derivatives at the wall. Hence, as a main consequence, the formula might not be suitable as toy model for certain theoretical purposes. The second drawback, which is also another consequence of the same fact, is that it can be used as thermal wall function only for
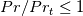 , as higher values will tend to amplify the part of the profile which is uncorrect.
, as higher values will tend to amplify the part of the profile which is uncorrect.To overcome such issues, i follow here the same steps as before but with a different formulation for
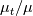 , using one which can be integrated exactly. We start from the temperature equation, which is more general:
, using one which can be integrated exactly. We start from the temperature equation, which is more general:![\frac{d}{dy}\left[C_p\left(\frac{\mu}{Pr}+\frac{\mu_t}{Pr_t}\right)\frac{dT}{dy}\right]=F_T \frac{d}{dy}\left[C_p\left(\frac{\mu}{Pr}+\frac{\mu_t}{Pr_t}\right)\frac{dT}{dy}\right]=F_T](/Forums/vbLatex/img/0a6ecf7d1a227b166f5e9fa4142c0df0-1.gif)
where
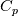 (constant pressure specific heat),
(constant pressure specific heat), 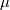 (dynamic viscosity),
(dynamic viscosity), 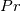 (Prandtl number),
(Prandtl number), 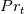 (turbulent Prandtl number) and
(turbulent Prandtl number) and 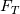 (defined in the following) are all constant. The fact that this equation correctly represents a large set of velocity/temperature viscous boundary conditions should be self-evident. For example,
(defined in the following) are all constant. The fact that this equation correctly represents a large set of velocity/temperature viscous boundary conditions should be self-evident. For example, 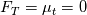 gives the classical linear relationship for the temperature (which becomes the one for the velocity when
gives the classical linear relationship for the temperature (which becomes the one for the velocity when 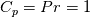 ). Also,
). Also, 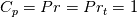 with
with 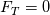 leads to the classical wall-function formulation (for certain forms of
leads to the classical wall-function formulation (for certain forms of 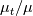 ). According to the specific equation form,
). According to the specific equation form, 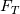 can have different meanings. For example, in the case of the velocity, it can include the wall-parallel pressure gradient (note that y is assumed to be the wall-normal coordinate, x the wall parallel one), the buoyancy term, etc. In general, it can include any of the terms that have been neglected in the LHS for the given equation. The only assumption here is that they are assumed constant along y (as will be shown in the following, it turns out that this can be actually relaxed).
can have different meanings. For example, in the case of the velocity, it can include the wall-parallel pressure gradient (note that y is assumed to be the wall-normal coordinate, x the wall parallel one), the buoyancy term, etc. In general, it can include any of the terms that have been neglected in the LHS for the given equation. The only assumption here is that they are assumed constant along y (as will be shown in the following, it turns out that this can be actually relaxed).The first step to proceed is integrating the equation above once. This produces (using
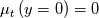 ):
):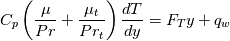
where
 (the
(the 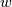 underscore meaning that it is evaluated at the wall, i.e., for
underscore meaning that it is evaluated at the wall, i.e., for 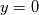 ). Multiplying by
). Multiplying by 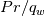 and rearranging, we obtain:
and rearranging, we obtain:![\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]\frac{dT^+}{dy^+}=Pr\left(1+F_T^+y^+\right) \left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]\frac{dT^+}{dy^+}=Pr\left(1+F_T^+y^+\right)](/Forums/vbLatex/img/ec0a7c6b314f4985a4a3a82352ec320a-1.gif)
where:
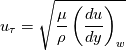
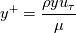
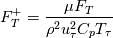

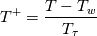
The same equation, interpreted for the velocity, would read:
![\left[1+\left(\frac{\mu_t}{\mu}\right)\right]\frac{du^+}{dy^+}=1+F_u^+y^+ \left[1+\left(\frac{\mu_t}{\mu}\right)\right]\frac{du^+}{dy^+}=1+F_u^+y^+](/Forums/vbLatex/img/57d73cd8f878e13b4d81fb3f811f02b8-1.gif)
where
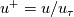 . This confirms that the temperature solution can also be used for the velocity by a proper interpretation of the terms. Going back to the temperature equation, we then end up with the following equation for the nondimensional temperature derivative:
. This confirms that the temperature solution can also be used for the velocity by a proper interpretation of the terms. Going back to the temperature equation, we then end up with the following equation for the nondimensional temperature derivative:![\frac{dT^+}{dy^+}=\frac{Pr\left(1+F_T^+y^+\right)}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]} \frac{dT^+}{dy^+}=\frac{Pr\left(1+F_T^+y^+\right)}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}](/Forums/vbLatex/img/6f93b3151b1a95e271960766dd7c8d1d-1.gif)
Then, by a further integration:
![T^+\left(y^+\right)=Pr \left\{\int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}+\int_0^{y+}{\frac{F_T^+z^+}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}\right\} T^+\left(y^+\right)=Pr \left\{\int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}+\int_0^{y+}{\frac{F_T^+z^+}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}\right\}](/Forums/vbLatex/img/43b30907ca252d9284af261112e8653c-1.gif)
Note that i temporarily suspended the hypothesis that
 is constant. Now, let us also assume that we know the first integral, that is:
is constant. Now, let us also assume that we know the first integral, that is:![\int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}=f^+\left(y^+\right) \int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}=f^+\left(y^+\right)](/Forums/vbLatex/img/d6d88feb731c9f2583155cd1349c99c1-1.gif)
is a known function. Then, the solution becomes:
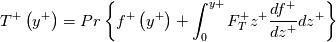
And after integration by parts:
![T^+\left(y^+\right)=Pr f^+\left(y^+\right)\left[1+F_T^+\left(y^+\right)y^+\right]-Pr\int_0^{y+}{f^+\left(F_T^++z^+\frac{dF_T^+}{dz^+}\right)dz^+} T^+\left(y^+\right)=Pr f^+\left(y^+\right)\left[1+F_T^+\left(y^+\right)y^+\right]-Pr\int_0^{y+}{f^+\left(F_T^++z^+\frac{dF_T^+}{dz^+}\right)dz^+}](/Forums/vbLatex/img/5ed4ad339bab706754cd2a99cb0c126e-1.gif)
For the sake of conciseness, let us also assume:
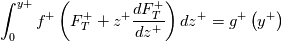
so that the full solution is:
![T^+\left(y^+\right)=Pr f^+\left(y^+\right)\left[1+F_T^+\left(y^+\right)y^+\right]-Pr g^+\left(y^+\right) T^+\left(y^+\right)=Pr f^+\left(y^+\right)\left[1+F_T^+\left(y^+\right)y^+\right]-Pr g^+\left(y^+\right)](/Forums/vbLatex/img/6ec7643a353ba9475910f82c1482acbf-1.gif)
While we have just moved the original problem to that of solving the two integrals for
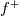 and
and 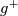 , those will actually turn out to be easier to solve. Note also that the parenthesis in
, those will actually turn out to be easier to solve. Note also that the parenthesis in 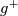 is a polynomial of the same order of
is a polynomial of the same order of  (assuming that it is approximated with a certain degree polynomial). Particularly relevant is the case with
(assuming that it is approximated with a certain degree polynomial). Particularly relevant is the case with  constant (as is typically assumed). However, note that ,for the
constant (as is typically assumed). However, note that ,for the 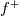 that we are going to derive below, a linear approximation is also integrable, as well as any other polynomial of higher degree. Obviously, things rapidly become cumbersome, with the degree of the polynomial, so for the present purposes it is sufficient to go back to the case
that we are going to derive below, a linear approximation is also integrable, as well as any other polynomial of higher degree. Obviously, things rapidly become cumbersome, with the degree of the polynomial, so for the present purposes it is sufficient to go back to the case  constant. In this case
constant. In this case 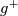 is simply the integral of
is simply the integral of 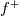 times
times  . Note that Popovac and Hanjalic have shown (for the velocity) that this is actually relevant for several practical cases. Nonetheless, is worth remembering that this is not a costriction of the present approach (probably it wasn't neither when
. Note that Popovac and Hanjalic have shown (for the velocity) that this is actually relevant for several practical cases. Nonetheless, is worth remembering that this is not a costriction of the present approach (probably it wasn't neither when 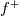 was based on the Reichardt profile).
was based on the Reichardt profile).So, at this point we are left with determining
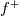 . To this end, we need a model for
. To this end, we need a model for 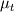 . Note that this is not different from the approach used by Van Driest to determine his velocity profile. It's just that the mixing length hypothesis he used led to a non integrable function. The same also happened to Reichardt, who then started modificating his function until something integrable came out.
. Note that this is not different from the approach used by Van Driest to determine his velocity profile. It's just that the mixing length hypothesis he used led to a non integrable function. The same also happened to Reichardt, who then started modificating his function until something integrable came out.To overcome this limit, here we abandon those formulations and use instead the one from Musker:
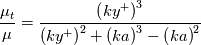
with
 being, in its original formulation, a constant (see below). It is worth mentioning that this functional form respects both the
being, in its original formulation, a constant (see below). It is worth mentioning that this functional form respects both the 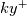 behavior for
behavior for 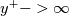 and the
and the 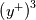 behavior for
behavior for  .
.Note also that the Spalart-Allmaras model has a simlar behavior near the wall (see Allmaras et al., ICCFD 2012):
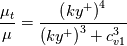
which then fails to recover the correct
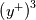 behavior for
behavior for  (However, Spalart and Allmaras explicitly mention in their original 1994 work that thay didn't notice any meaningful difference deriving from using this specific form instead of a correct one, say, the mixing length). This just to say that the Musker form is not only meaningful, but also representative of the near wall behavior of the Spalart-Allmaras model.
(However, Spalart and Allmaras explicitly mention in their original 1994 work that thay didn't notice any meaningful difference deriving from using this specific form instead of a correct one, say, the mixing length). This just to say that the Musker form is not only meaningful, but also representative of the near wall behavior of the Spalart-Allmaras model.To solve for
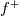 with the Musker turbulent viscosity, we first consider the case
with the Musker turbulent viscosity, we first consider the case 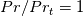 , as this already has a known solution, provided in its most general form by Monkewitz et al. (POF 20, 105102, 2008):
, as this already has a known solution, provided in its most general form by Monkewitz et al. (POF 20, 105102, 2008):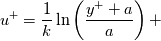
![\frac{\alpha}{a+4\alpha}\left\{\left(a-4\alpha\right)\ln\left[\frac{a\left[\left(y^+-\alpha\right)^2+\beta^2\right]}{2\alpha\left(y^++a\right)^2}\right]+\gamma\left[\arctan\left(\frac{y^+-\alpha}{\beta}\right)+\arctan\left(\frac{\alpha}{\beta}\right)\right]\right\} \frac{\alpha}{a+4\alpha}\left\{\left(a-4\alpha\right)\ln\left[\frac{a\left[\left(y^+-\alpha\right)^2+\beta^2\right]}{2\alpha\left(y^++a\right)^2}\right]+\gamma\left[\arctan\left(\frac{y^+-\alpha}{\beta}\right)+\arctan\left(\frac{\alpha}{\beta}\right)\right]\right\}](/Forums/vbLatex/img/555f1e220bd91848e372424c88a2ca07-1.gif)
where:
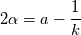
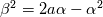
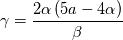
The constant
 is found by calibration with the turbulent velocity profile. Monkewitz et al. use
is found by calibration with the turbulent velocity profile. Monkewitz et al. use 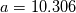 . In contrast, i calibrated the constant using the mixing length model with a constant
. In contrast, i calibrated the constant using the mixing length model with a constant 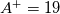 , resulting in
, resulting in 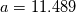 .
.Now, the whole point of the procedure is: how to extend such formulation to the case
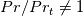 ? See part 2
? See part 2Total Comments 0





