A generalized thermal/dynamic wall function: Part 3
In this post i summarize the initial problem and the procedure to determine the wall function value (i.e., the solution) for given 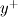 ,
, ,
,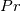 and
and 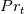 .
.
We looked for a solution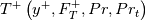 to the problem:
to the problem:
![\frac{dT^+}{dy^+}=\frac{Pr\left(1+F_T^+y^+\right)}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]} \frac{dT^+}{dy^+}=\frac{Pr\left(1+F_T^+y^+\right)}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}](/Forums/vbLatex/img/6f93b3151b1a95e271960766dd7c8d1d-1.gif)
with:
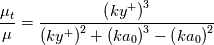
for given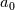 . This represents, in nondimensional form, a certain set of viscous boundary conditions for velocity/temperature. In practice,
. This represents, in nondimensional form, a certain set of viscous boundary conditions for velocity/temperature. In practice, 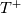 is a wall-function. The solution is given by:
is a wall-function. The solution is given by:
![T^+=Pr \left[f^+\left(1 +F_T^+y^+\right)-g^+\right] T^+=Pr \left[f^+\left(1 +F_T^+y^+\right)-g^+\right]](/Forums/vbLatex/img/f3c170727c6edd66978d053ebcaa9c27-1.gif)
Where,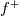 is given by:
is given by:
![f^+=\int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}=\frac{Pr_t}{kPr}\ln\left(\frac{y^++a}{a}\right)+ f^+=\int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}=\frac{Pr_t}{kPr}\ln\left(\frac{y^++a}{a}\right)+](/Forums/vbLatex/img/c51e02b828e4362aaf78db892b7d6851-1.gif)
![\frac{\alpha}{a+4\alpha}\left\{\left(a-4\alpha\right)\ln\left[\frac{a\left[\left(y^+-\alpha\right)^2+\beta^2\right]}{2\alpha\left(y^++a\right)^2}\right]+\gamma\left[\arctan\left(\frac{y^+-\alpha}{\beta}\right)+\arctan\left(\frac{\alpha}{\beta}\right)\right]\right\} \frac{\alpha}{a+4\alpha}\left\{\left(a-4\alpha\right)\ln\left[\frac{a\left[\left(y^+-\alpha\right)^2+\beta^2\right]}{2\alpha\left(y^++a\right)^2}\right]+\gamma\left[\arctan\left(\frac{y^+-\alpha}{\beta}\right)+\arctan\left(\frac{\alpha}{\beta}\right)\right]\right\}](/Forums/vbLatex/img/555f1e220bd91848e372424c88a2ca07-1.gif)
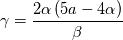
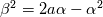
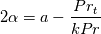
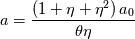
![\eta = \sqrt[3]{1+\theta\left(\psi+\sqrt{\psi^2+\phi}\right)} \eta = \sqrt[3]{1+\theta\left(\psi+\sqrt{\psi^2+\phi}\right)}](/Forums/vbLatex/img/f2fcd46b8600cca0cf70bb0a2e3bf6fb-1.gif)
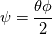
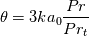
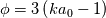
and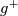 is given by a (typically) straightforward integration:
is given by a (typically) straightforward integration:
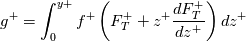
In practice, given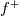 above, the integral in
above, the integral in 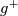 is easily computable for
is easily computable for  in the form of a polynomial of arbitrary degree. For the sake of conciseness we only considered
in the form of a polynomial of arbitrary degree. For the sake of conciseness we only considered  as constant, the resulting integral being
as constant, the resulting integral being  times the following function:
times the following function:
https://www.wolframalpha.com/input/?...Batan(b%2Fc)))
The whole procedure is implemented in the attached MATLAB/Octave script, where the analytical solution above (ta) is compared with the numerical one (tn), obtained by numerically integrating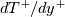 .
.
The usage should be straightforward:
1) Pick up values for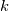 ,
,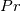 ,
,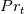 and
and  (lines 8-11).
(lines 8-11).
2) Choose plotting options (lines 5-6)
3) Choose how many points you want to use to integrate numerically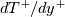 (line 7).
(line 7).
4) Run the script.
Note that the constant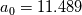 has been calibrated using as reference the mixing length model with a constant
has been calibrated using as reference the mixing length model with a constant 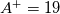 . The relative turbulent mixing length viscosity has been left commented in the script (line 60), so that you can use it to calibrate the model for different values of the constant (line 13). Note that the calibration is always done once using
. The relative turbulent mixing length viscosity has been left commented in the script (line 60), so that you can use it to calibrate the model for different values of the constant (line 13). Note that the calibration is always done once using  and
and 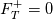 . After that, any value of those parameters will be taken into account automatically by the formula.
. After that, any value of those parameters will be taken into account automatically by the formula.
In general, the value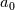 is such that
is such that 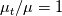 at
at 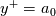 . Hence, it could be also used as a mean to introduce roughness effects in the formulation.
. Hence, it could be also used as a mean to introduce roughness effects in the formulation.
In conclusion, it is worth mentioning what are the limitations of the present wall function with respect to the full solution of the turbulent equations with, say, the SA model:
1) The equations are not in their full form, but in the incompressible TBLE form, with constant RHS.
2) The underlying turbulent viscosity model is not formally sensitized to the pressure gradient.
However, note that the same limitations also apply to, say:
K. Suga et al. / Int. J. Heat and Fluid Flow 27 (2006) 852–866
which provides a relation similar to the present one but with a higher approximation on the turbulent viscosity.
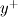 ,
, ,
,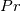 and
and 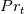 .
.We looked for a solution
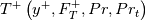 to the problem:
to the problem:![\frac{dT^+}{dy^+}=\frac{Pr\left(1+F_T^+y^+\right)}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]} \frac{dT^+}{dy^+}=\frac{Pr\left(1+F_T^+y^+\right)}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}](/Forums/vbLatex/img/6f93b3151b1a95e271960766dd7c8d1d-1.gif)
with:
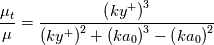
for given
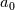 . This represents, in nondimensional form, a certain set of viscous boundary conditions for velocity/temperature. In practice,
. This represents, in nondimensional form, a certain set of viscous boundary conditions for velocity/temperature. In practice, 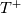 is a wall-function. The solution is given by:
is a wall-function. The solution is given by:![T^+=Pr \left[f^+\left(1 +F_T^+y^+\right)-g^+\right] T^+=Pr \left[f^+\left(1 +F_T^+y^+\right)-g^+\right]](/Forums/vbLatex/img/f3c170727c6edd66978d053ebcaa9c27-1.gif)
Where,
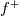 is given by:
is given by:![f^+=\int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}=\frac{Pr_t}{kPr}\ln\left(\frac{y^++a}{a}\right)+ f^+=\int_0^{y+}{\frac{1}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz^+}=\frac{Pr_t}{kPr}\ln\left(\frac{y^++a}{a}\right)+](/Forums/vbLatex/img/c51e02b828e4362aaf78db892b7d6851-1.gif)
![\frac{\alpha}{a+4\alpha}\left\{\left(a-4\alpha\right)\ln\left[\frac{a\left[\left(y^+-\alpha\right)^2+\beta^2\right]}{2\alpha\left(y^++a\right)^2}\right]+\gamma\left[\arctan\left(\frac{y^+-\alpha}{\beta}\right)+\arctan\left(\frac{\alpha}{\beta}\right)\right]\right\} \frac{\alpha}{a+4\alpha}\left\{\left(a-4\alpha\right)\ln\left[\frac{a\left[\left(y^+-\alpha\right)^2+\beta^2\right]}{2\alpha\left(y^++a\right)^2}\right]+\gamma\left[\arctan\left(\frac{y^+-\alpha}{\beta}\right)+\arctan\left(\frac{\alpha}{\beta}\right)\right]\right\}](/Forums/vbLatex/img/555f1e220bd91848e372424c88a2ca07-1.gif)
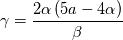
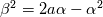
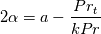
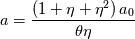
![\eta = \sqrt[3]{1+\theta\left(\psi+\sqrt{\psi^2+\phi}\right)} \eta = \sqrt[3]{1+\theta\left(\psi+\sqrt{\psi^2+\phi}\right)}](/Forums/vbLatex/img/f2fcd46b8600cca0cf70bb0a2e3bf6fb-1.gif)
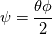
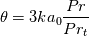
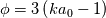
and
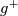 is given by a (typically) straightforward integration:
is given by a (typically) straightforward integration: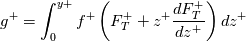
In practice, given
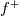 above, the integral in
above, the integral in 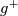 is easily computable for
is easily computable for  in the form of a polynomial of arbitrary degree. For the sake of conciseness we only considered
in the form of a polynomial of arbitrary degree. For the sake of conciseness we only considered  as constant, the resulting integral being
as constant, the resulting integral being  times the following function:
times the following function:https://www.wolframalpha.com/input/?...Batan(b%2Fc)))
The whole procedure is implemented in the attached MATLAB/Octave script, where the analytical solution above (ta) is compared with the numerical one (tn), obtained by numerically integrating
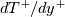 .
.The usage should be straightforward:
1) Pick up values for
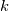 ,
,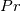 ,
,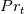 and
and  (lines 8-11).
(lines 8-11).2) Choose plotting options (lines 5-6)
3) Choose how many points you want to use to integrate numerically
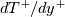 (line 7).
(line 7).4) Run the script.
Note that the constant
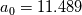 has been calibrated using as reference the mixing length model with a constant
has been calibrated using as reference the mixing length model with a constant 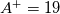 . The relative turbulent mixing length viscosity has been left commented in the script (line 60), so that you can use it to calibrate the model for different values of the constant (line 13). Note that the calibration is always done once using
. The relative turbulent mixing length viscosity has been left commented in the script (line 60), so that you can use it to calibrate the model for different values of the constant (line 13). Note that the calibration is always done once using  and
and 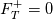 . After that, any value of those parameters will be taken into account automatically by the formula.
. After that, any value of those parameters will be taken into account automatically by the formula.In general, the value
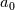 is such that
is such that 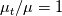 at
at 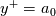 . Hence, it could be also used as a mean to introduce roughness effects in the formulation.
. Hence, it could be also used as a mean to introduce roughness effects in the formulation.In conclusion, it is worth mentioning what are the limitations of the present wall function with respect to the full solution of the turbulent equations with, say, the SA model:
1) The equations are not in their full form, but in the incompressible TBLE form, with constant RHS.
2) The underlying turbulent viscosity model is not formally sensitized to the pressure gradient.
However, note that the same limitations also apply to, say:
K. Suga et al. / Int. J. Heat and Fluid Flow 27 (2006) 852–866
which provides a relation similar to the present one but with a higher approximation on the turbulent viscosity.
Total Comments 0





