Closing on wall functions - part 1: Problem statement and general solution
This is the last series of posts on wall functions, where I summarize previous findings and give them a broader context. I won't provide derivations (hopefully I'll have time to put this in a larger note), but just few statements with the proper scripts to test them.
This all started with the aim to solve the following problem:
![\frac{d}{dy}\left[C_p\left(\frac{\mu}{Pr}+\frac{\mu_t}{Pr_t}\right)\frac{dT}{dy}\right]=F_T \frac{d}{dy}\left[C_p\left(\frac{\mu}{Pr}+\frac{\mu_t}{Pr_t}\right)\frac{dT}{dy}\right]=F_T](/Forums/vbLatex/img/0a6ecf7d1a227b166f5e9fa4142c0df0-1.gif)
with boundary conditions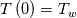 and
and 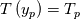 . Here,
. Here, 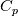 (constant pressure specific heat),
(constant pressure specific heat), 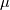 (dynamic viscosity),
(dynamic viscosity), 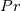 (Prandtl number) and
(Prandtl number) and 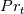 (turbulent Prandtl number) are all constant and
(turbulent Prandtl number) are all constant and 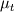 is an user specified turbulent viscosity profile better defined later. My previous attempts used a constant
is an user specified turbulent viscosity profile better defined later. My previous attempts used a constant 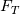 too, here the more general case:
too, here the more general case:
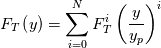
is considered. The fact that this equation correctly represents a large set of velocity/temperature viscous boundary conditions should be self-evident (and you can read previous posts on the matter for explanations). Omitting derivations, assuming also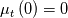 , the formal solution to the problem above can be written as:
, the formal solution to the problem above can be written as:
![T\left(y\right) = T_w + y \left(\frac{Pr}{\mu C_p}\right) \left[q_w\left(\frac{{s_T^{-1}}^+}{y^+}\right)+y\sum_{i=0}^{N}\frac{F_T^i}{i+1}\left(\frac{y}{y_p}\right)^i\left(\frac{{s_T^i}^+}{{y^+}^{i+2}}\right)\right] T\left(y\right) = T_w + y \left(\frac{Pr}{\mu C_p}\right) \left[q_w\left(\frac{{s_T^{-1}}^+}{y^+}\right)+y\sum_{i=0}^{N}\frac{F_T^i}{i+1}\left(\frac{y}{y_p}\right)^i\left(\frac{{s_T^i}^+}{{y^+}^{i+2}}\right)\right]](/Forums/vbLatex/img/9237a956ebcae57d242290e7f9deaee2-1.gif)
where (note the sign opposite to the classical thermal convention, but coherent to the velocity one, for ease of exposition):
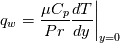 .
.
It also imemdiately follows that:
![q_w = \frac{\left\{\frac{\left[T\left(y\right) - T_w\right]}{y} \left(\frac{\mu C_p}{Pr}\right) - y\sum_{i=0}^{N}\frac{F_T^i}{i+1}\left(\frac{y}{y_p}\right)^i\left(\frac{{s_T^i}^+}{{y^+}^{i+2}}\right) \right\}}{\left(\frac{{s_T^{-1}}^+}{y^+}\right)} q_w = \frac{\left\{\frac{\left[T\left(y\right) - T_w\right]}{y} \left(\frac{\mu C_p}{Pr}\right) - y\sum_{i=0}^{N}\frac{F_T^i}{i+1}\left(\frac{y}{y_p}\right)^i\left(\frac{{s_T^i}^+}{{y^+}^{i+2}}\right) \right\}}{\left(\frac{{s_T^{-1}}^+}{y^+}\right)}](/Forums/vbLatex/img/d39639a33645aea7c368cd58ffa68530-1.gif)
The functions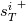 appearing above are defined as follows:
appearing above are defined as follows:
![{s_T^i}^+ = \int_0^{y+}{\frac{z^{i+1}}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz} {s_T^i}^+ = \int_0^{y+}{\frac{z^{i+1}}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz}](/Forums/vbLatex/img/ad9fb961629ffcde37a227cf379b8477-1.gif)
All the expressions above hold true for the velocity case as well, provided that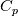 ,
, 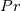 and
and 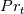 are all set to 1 (in this case, for clarity, we denote the functions above as
are all set to 1 (in this case, for clarity, we denote the functions above as 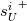 ). The average turbulent kinetic energy production can instead be shown to be:
). The average turbulent kinetic energy production can instead be shown to be:
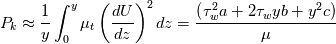
where:
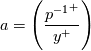
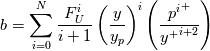
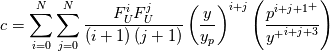
and the functions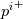 appearing above are defined as follows:
appearing above are defined as follows:
![{p^i}^+ = \int_0^{y+}{\frac{z^{i+1}\left(\frac{\mu_t}{\mu}\right)}{\left[1+\left(\frac{\mu_t}{\mu}\right)\right]^2}dz} {p^i}^+ = \int_0^{y+}{\frac{z^{i+1}\left(\frac{\mu_t}{\mu}\right)}{\left[1+\left(\frac{\mu_t}{\mu}\right)\right]^2}dz}](/Forums/vbLatex/img/36fd1c56e5642ffc4df02d8cc199c556-1.gif)
It is worth mentioning that, at this point, the formulas above are still exact for the initial problem statement, and all the details of the specific solution method have been moved to the integrals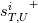 and
and 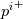 . This, while kind of obvious, is still remarkable, as it suggests a very specific implementation for wall functions and wall bcs in general, as the formulas above are straightforward generalizations of classical laminar formulas. Note also, that we have introduced an
. This, while kind of obvious, is still remarkable, as it suggests a very specific implementation for wall functions and wall bcs in general, as the formulas above are straightforward generalizations of classical laminar formulas. Note also, that we have introduced an 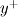 but it just appears as extreme of the integrals and as their denominator (elevated to a certain power). In practice, it is the variable that appears in the
but it just appears as extreme of the integrals and as their denominator (elevated to a certain power). In practice, it is the variable that appears in the 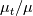 formula, but nothing more needed to be specified about it in order to obtain the formulas above. In general, it will have a formula like
formula, but nothing more needed to be specified about it in order to obtain the formulas above. In general, it will have a formula like 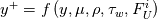 , but could well just depend from the tubulent model variables.
, but could well just depend from the tubulent model variables.
Leaving aside, for the moment, the solution for the integrals above (we assume the availability of a routine that gives their value for given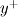 ), the general solution procedure would be as follows:
), the general solution procedure would be as follows:
In practice, as will be clear in a moment, I suggest to have routines that actually return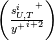 and
and 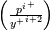 , as it is their ratio that needs to be computed. Also, for reasons that will be clear in the second post of this series, I anticipate here that for the iterative solution of
, as it is their ratio that needs to be computed. Also, for reasons that will be clear in the second post of this series, I anticipate here that for the iterative solution of  in step 1 above, it is useful to have the same routine for
in step 1 above, it is useful to have the same routine for 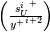 to also return:
to also return:
![{q^i}^+ = \frac{\left[\frac{1}{1+\frac{\mu_t}{\mu}}-\left(i+2\right)\left(\frac{{s_U^i}^+}{{y^+}^{i+2}}\right)\right]}{{y^+}^2} {q^i}^+ = \frac{\left[\frac{1}{1+\frac{\mu_t}{\mu}}-\left(i+2\right)\left(\frac{{s_U^i}^+}{{y^+}^{i+2}}\right)\right]}{{y^+}^2}](/Forums/vbLatex/img/4edab6fab0de4e7a8cf594f384f9fdca-1.gif)
which is the only wall function specific term entering in the derivative for the iterative procedure. I conclude this first post by stating, without proof, that for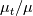 going to 0 as
going to 0 as 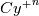 with
with 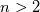 , all the above terms can be safely computed also for
, all the above terms can be safely computed also for 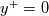 and their exact limits are:
and their exact limits are:
![\lim_{y^+\to 0}\left(\frac{{s_T^i}^+}{{y^+}^{i+2}}\right) = \lim_{y^+\to 0} \left[\frac{1}{\left(i+2\right)}-\left(\frac{Pr}{Pr_t}\right)\frac{C{y^+}^n}{\left(i+n+2\right)}\right] = \frac{1}{\left(i+2\right)} \lim_{y^+\to 0}\left(\frac{{s_T^i}^+}{{y^+}^{i+2}}\right) = \lim_{y^+\to 0} \left[\frac{1}{\left(i+2\right)}-\left(\frac{Pr}{Pr_t}\right)\frac{C{y^+}^n}{\left(i+n+2\right)}\right] = \frac{1}{\left(i+2\right)}](/Forums/vbLatex/img/02365018227767a69b51a38eff3a83ce-1.gif)
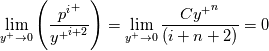
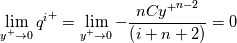
The second post in the series will formalize the iterative procedure for computing .
.
This all started with the aim to solve the following problem:
![\frac{d}{dy}\left[C_p\left(\frac{\mu}{Pr}+\frac{\mu_t}{Pr_t}\right)\frac{dT}{dy}\right]=F_T \frac{d}{dy}\left[C_p\left(\frac{\mu}{Pr}+\frac{\mu_t}{Pr_t}\right)\frac{dT}{dy}\right]=F_T](/Forums/vbLatex/img/0a6ecf7d1a227b166f5e9fa4142c0df0-1.gif)
with boundary conditions
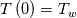 and
and 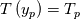 . Here,
. Here, 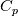 (constant pressure specific heat),
(constant pressure specific heat), 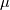 (dynamic viscosity),
(dynamic viscosity), 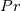 (Prandtl number) and
(Prandtl number) and 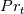 (turbulent Prandtl number) are all constant and
(turbulent Prandtl number) are all constant and 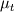 is an user specified turbulent viscosity profile better defined later. My previous attempts used a constant
is an user specified turbulent viscosity profile better defined later. My previous attempts used a constant 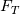 too, here the more general case:
too, here the more general case: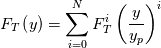
is considered. The fact that this equation correctly represents a large set of velocity/temperature viscous boundary conditions should be self-evident (and you can read previous posts on the matter for explanations). Omitting derivations, assuming also
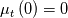 , the formal solution to the problem above can be written as:
, the formal solution to the problem above can be written as:![T\left(y\right) = T_w + y \left(\frac{Pr}{\mu C_p}\right) \left[q_w\left(\frac{{s_T^{-1}}^+}{y^+}\right)+y\sum_{i=0}^{N}\frac{F_T^i}{i+1}\left(\frac{y}{y_p}\right)^i\left(\frac{{s_T^i}^+}{{y^+}^{i+2}}\right)\right] T\left(y\right) = T_w + y \left(\frac{Pr}{\mu C_p}\right) \left[q_w\left(\frac{{s_T^{-1}}^+}{y^+}\right)+y\sum_{i=0}^{N}\frac{F_T^i}{i+1}\left(\frac{y}{y_p}\right)^i\left(\frac{{s_T^i}^+}{{y^+}^{i+2}}\right)\right]](/Forums/vbLatex/img/9237a956ebcae57d242290e7f9deaee2-1.gif)
where (note the sign opposite to the classical thermal convention, but coherent to the velocity one, for ease of exposition):
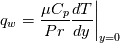 .
.It also imemdiately follows that:
![q_w = \frac{\left\{\frac{\left[T\left(y\right) - T_w\right]}{y} \left(\frac{\mu C_p}{Pr}\right) - y\sum_{i=0}^{N}\frac{F_T^i}{i+1}\left(\frac{y}{y_p}\right)^i\left(\frac{{s_T^i}^+}{{y^+}^{i+2}}\right) \right\}}{\left(\frac{{s_T^{-1}}^+}{y^+}\right)} q_w = \frac{\left\{\frac{\left[T\left(y\right) - T_w\right]}{y} \left(\frac{\mu C_p}{Pr}\right) - y\sum_{i=0}^{N}\frac{F_T^i}{i+1}\left(\frac{y}{y_p}\right)^i\left(\frac{{s_T^i}^+}{{y^+}^{i+2}}\right) \right\}}{\left(\frac{{s_T^{-1}}^+}{y^+}\right)}](/Forums/vbLatex/img/d39639a33645aea7c368cd58ffa68530-1.gif)
The functions
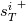 appearing above are defined as follows:
appearing above are defined as follows:![{s_T^i}^+ = \int_0^{y+}{\frac{z^{i+1}}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz} {s_T^i}^+ = \int_0^{y+}{\frac{z^{i+1}}{\left[1+\left(\frac{Pr}{Pr_t}\right)\left(\frac{\mu_t}{\mu}\right)\right]}dz}](/Forums/vbLatex/img/ad9fb961629ffcde37a227cf379b8477-1.gif)
All the expressions above hold true for the velocity case as well, provided that
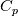 ,
, 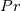 and
and 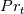 are all set to 1 (in this case, for clarity, we denote the functions above as
are all set to 1 (in this case, for clarity, we denote the functions above as 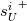 ). The average turbulent kinetic energy production can instead be shown to be:
). The average turbulent kinetic energy production can instead be shown to be: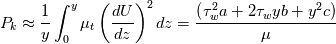
where:
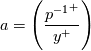
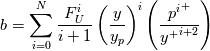
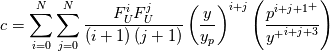
and the functions
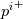 appearing above are defined as follows:
appearing above are defined as follows:![{p^i}^+ = \int_0^{y+}{\frac{z^{i+1}\left(\frac{\mu_t}{\mu}\right)}{\left[1+\left(\frac{\mu_t}{\mu}\right)\right]^2}dz} {p^i}^+ = \int_0^{y+}{\frac{z^{i+1}\left(\frac{\mu_t}{\mu}\right)}{\left[1+\left(\frac{\mu_t}{\mu}\right)\right]^2}dz}](/Forums/vbLatex/img/36fd1c56e5642ffc4df02d8cc199c556-1.gif)
It is worth mentioning that, at this point, the formulas above are still exact for the initial problem statement, and all the details of the specific solution method have been moved to the integrals
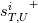 and
and 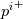 . This, while kind of obvious, is still remarkable, as it suggests a very specific implementation for wall functions and wall bcs in general, as the formulas above are straightforward generalizations of classical laminar formulas. Note also, that we have introduced an
. This, while kind of obvious, is still remarkable, as it suggests a very specific implementation for wall functions and wall bcs in general, as the formulas above are straightforward generalizations of classical laminar formulas. Note also, that we have introduced an 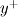 but it just appears as extreme of the integrals and as their denominator (elevated to a certain power). In practice, it is the variable that appears in the
but it just appears as extreme of the integrals and as their denominator (elevated to a certain power). In practice, it is the variable that appears in the 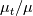 formula, but nothing more needed to be specified about it in order to obtain the formulas above. In general, it will have a formula like
formula, but nothing more needed to be specified about it in order to obtain the formulas above. In general, it will have a formula like 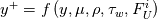 , but could well just depend from the tubulent model variables.
, but could well just depend from the tubulent model variables.Leaving aside, for the moment, the solution for the integrals above (we assume the availability of a routine that gives their value for given
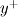 ), the general solution procedure would be as follows:
), the general solution procedure would be as follows:- Solve equation above for
 (iteratively, if
(iteratively, if 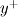 depends from it) using
depends from it) using  . Note that the equation for
. Note that the equation for  is obtained from the one for
is obtained from the one for 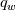 with
with 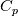 ,
, 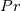 and
and 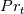 set to 1 and the functions
set to 1 and the functions 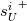 in place of the
in place of the 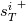 .
. - Determine
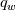 or
or 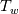 , depending from the available thermal bc, from the equations above using
, depending from the available thermal bc, from the equations above using  and the now certainly available
and the now certainly available 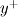 (either iteratively from first step or just from turbulent variables).
(either iteratively from first step or just from turbulent variables). - Repeat the previous point for any scalar (with
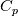 set to 1 and the Schmidt numbers in place of the Prandtl numbers, also within the s integrals)
set to 1 and the Schmidt numbers in place of the Prandtl numbers, also within the s integrals)
In practice, as will be clear in a moment, I suggest to have routines that actually return
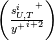 and
and 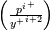 , as it is their ratio that needs to be computed. Also, for reasons that will be clear in the second post of this series, I anticipate here that for the iterative solution of
, as it is their ratio that needs to be computed. Also, for reasons that will be clear in the second post of this series, I anticipate here that for the iterative solution of  in step 1 above, it is useful to have the same routine for
in step 1 above, it is useful to have the same routine for 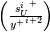 to also return:
to also return:![{q^i}^+ = \frac{\left[\frac{1}{1+\frac{\mu_t}{\mu}}-\left(i+2\right)\left(\frac{{s_U^i}^+}{{y^+}^{i+2}}\right)\right]}{{y^+}^2} {q^i}^+ = \frac{\left[\frac{1}{1+\frac{\mu_t}{\mu}}-\left(i+2\right)\left(\frac{{s_U^i}^+}{{y^+}^{i+2}}\right)\right]}{{y^+}^2}](/Forums/vbLatex/img/4edab6fab0de4e7a8cf594f384f9fdca-1.gif)
which is the only wall function specific term entering in the derivative for the iterative procedure. I conclude this first post by stating, without proof, that for
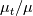 going to 0 as
going to 0 as 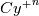 with
with 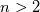 , all the above terms can be safely computed also for
, all the above terms can be safely computed also for 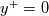 and their exact limits are:
and their exact limits are:![\lim_{y^+\to 0}\left(\frac{{s_T^i}^+}{{y^+}^{i+2}}\right) = \lim_{y^+\to 0} \left[\frac{1}{\left(i+2\right)}-\left(\frac{Pr}{Pr_t}\right)\frac{C{y^+}^n}{\left(i+n+2\right)}\right] = \frac{1}{\left(i+2\right)} \lim_{y^+\to 0}\left(\frac{{s_T^i}^+}{{y^+}^{i+2}}\right) = \lim_{y^+\to 0} \left[\frac{1}{\left(i+2\right)}-\left(\frac{Pr}{Pr_t}\right)\frac{C{y^+}^n}{\left(i+n+2\right)}\right] = \frac{1}{\left(i+2\right)}](/Forums/vbLatex/img/02365018227767a69b51a38eff3a83ce-1.gif)
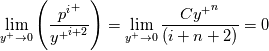
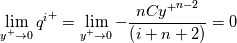
The second post in the series will formalize the iterative procedure for computing
 .
.Total Comments 0





