Closing on wall functions - part 2: the iterative procedure
The first step in the wall function approach delineated in the first post of this series requires determining  from
from
![\tau_w = \frac{\left[\left(U_p - U_w\right) \left(\frac{\mu}{y_p}\right) - y_p\sum_{i=0}^{N}\frac{F_U^i}{i+1}\left(\frac{{s_U^i}^+}{{y^+}^{i+2}}\right)\bigg\rvert_{y_p^+} \right]}{\left(\frac{{s_U^{-1}}^+}{y^+}\right)\bigg\rvert_{y_p^+}} \tau_w = \frac{\left[\left(U_p - U_w\right) \left(\frac{\mu}{y_p}\right) - y_p\sum_{i=0}^{N}\frac{F_U^i}{i+1}\left(\frac{{s_U^i}^+}{{y^+}^{i+2}}\right)\bigg\rvert_{y_p^+} \right]}{\left(\frac{{s_U^{-1}}^+}{y^+}\right)\bigg\rvert_{y_p^+}}](/Forums/vbLatex/img/37611d6af86567f69bd2cd9bc179341c-1.gif)
with analogous steps also required for the temperature and scalars. If one has a mean to univocally/externally determine , then velocity, temperature and scalars are all equivalent and the relation above (properly adjusted for temperature and scalars) can be used in one shot to determine the wall flux (or the wall value if the flux is known). For
, then velocity, temperature and scalars are all equivalent and the relation above (properly adjusted for temperature and scalars) can be used in one shot to determine the wall flux (or the wall value if the flux is known). For 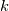 (turbulent kinetic energy) based turbulence models one can, for example, assume:
(turbulent kinetic energy) based turbulence models one can, for example, assume:
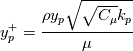
For the Spalart-Allmaras model instead, one can assume (it will be shown in a following post how this is, indeed, relevant):
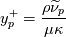
with the von Karman constant used in the model. These relations are strictly valid in equilibrium cases (
the von Karman constant used in the model. These relations are strictly valid in equilibrium cases (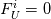 for all i) but are usually used in non equilibrium cases as well (there is a second advantage, besides non requiring iterations, that will be clear in a moment). If such variables/definitions are not available (say, in LES) one tipically defines:
for all i) but are usually used in non equilibrium cases as well (there is a second advantage, besides non requiring iterations, that will be clear in a moment). If such variables/definitions are not available (say, in LES) one tipically defines:
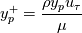
where:
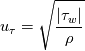
thus one ends up with an implcit non linear relation for that needs iterations to be resolved. Before going to the algorithmic part of these iterations, however, it is worth mentioning that the above choice for
that needs iterations to be resolved. Before going to the algorithmic part of these iterations, however, it is worth mentioning that the above choice for 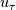 is largely inconvenient for non equilibrium flows, as the zero flux outcome is only possible when
is largely inconvenient for non equilibrium flows, as the zero flux outcome is only possible when 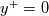 instead of, generally, when the numerator becomes 0 (which is the other advantage of the
instead of, generally, when the numerator becomes 0 (which is the other advantage of the 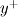 formulations based on turbulence variables). Following the relevant literature on the topic, we thus redefine the
formulations based on turbulence variables). Following the relevant literature on the topic, we thus redefine the 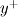 as follows*:
as follows*:
![y_p^+ = \frac{\rho y_p}{\mu} \sqrt{\frac{\left|\tau_w\right|}{\rho} + \sum_{i=0}^{N}\left[\frac{\mu \left|F_U^i\right|}{\rho^2\left(i+1\right)}\right]^{\frac{1}{3}}} = \sqrt{\left|\theta_p\right|+\sum_{i=0}^{N}\left|F_p^i\right|^{\frac{2}{3}}} y_p^+ = \frac{\rho y_p}{\mu} \sqrt{\frac{\left|\tau_w\right|}{\rho} + \sum_{i=0}^{N}\left[\frac{\mu \left|F_U^i\right|}{\rho^2\left(i+1\right)}\right]^{\frac{1}{3}}} = \sqrt{\left|\theta_p\right|+\sum_{i=0}^{N}\left|F_p^i\right|^{\frac{2}{3}}}](/Forums/vbLatex/img/e71e43f1f1e973669705e4e4234300fa-1.gif)
where we have introduced the nondimensional parameters:
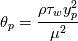
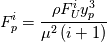
As both appear in the definition, it seems natural to transform the
definition, it seems natural to transform the  equation as well, by multiplying it with the factor
equation as well, by multiplying it with the factor 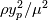 . The result is:
. The result is:
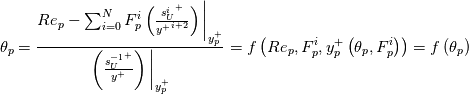
where we have introduced the additional nondimensional number:
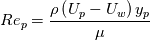
and highlighted the general dependence of the RHS of the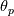 equation from
equation from 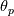 itself trough
itself trough  . Despite certainly having an extra
. Despite certainly having an extra 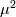 factor for all the terms (which could then be simplified to make all the numbers involved smaller), the advantage of this form is that being non dimensional it can be also solved once and for all for all the required nondimensional values and used at runtime as an interpolation table. Indeed, at this stage, it has to be reminded that the procedure is still applicable to generic
factor for all the terms (which could then be simplified to make all the numbers involved smaller), the advantage of this form is that being non dimensional it can be also solved once and for all for all the required nondimensional values and used at runtime as an interpolation table. Indeed, at this stage, it has to be reminded that the procedure is still applicable to generic 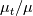 functions, and their integration might be costly as well. However, even in this case one would need to solve the equation above at least once for each set of relevant parameters. And having a nondimensional equation helps developing an iterative procedure.
functions, and their integration might be costly as well. However, even in this case one would need to solve the equation above at least once for each set of relevant parameters. And having a nondimensional equation helps developing an iterative procedure.
I have found that with the constant non equilibrium term only, for different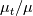 parameterizations, the above equation can be easily solved with a Newton-Raphson method with no more than 10 iterations (starting always from the same laminar solution, which is typically very wrong for high Re):
parameterizations, the above equation can be easily solved with a Newton-Raphson method with no more than 10 iterations (starting always from the same laminar solution, which is typically very wrong for high Re):
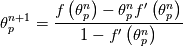
provided that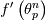 is set to 0 whenever it is equal or greater than 1. This specific modification, which reverts the method to fixed point iterations, is needed not only to avoid a possible division by 0, but also because the fixed point iterations will push the solution out of a problematic branch of the function.
is set to 0 whenever it is equal or greater than 1. This specific modification, which reverts the method to fixed point iterations, is needed not only to avoid a possible division by 0, but also because the fixed point iterations will push the solution out of a problematic branch of the function.
I provide, again without proof, the expression for the derivative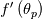 needed in the method:
needed in the method:
![f'\left(\theta_p\right) = -\frac{SIGN\left(\theta_p\right)}{2\left(\frac{{s_U^{-1}}^+}{y^+}\right)\bigg\rvert_{y_p^+}} \left[f\left(\theta_p\right) {q^{-1}}^+ + \sum_{i=0}^{N}F_p^i {q^i}^+\right] f'\left(\theta_p\right) = -\frac{SIGN\left(\theta_p\right)}{2\left(\frac{{s_U^{-1}}^+}{y^+}\right)\bigg\rvert_{y_p^+}} \left[f\left(\theta_p\right) {q^{-1}}^+ + \sum_{i=0}^{N}F_p^i {q^i}^+\right]](/Forums/vbLatex/img/392f03ceddf360c22c89f5a395003c64-1.gif)
where the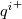 functions have been defined in the first post of this series.
functions have been defined in the first post of this series.
In equilibrium and favourable pressure gradient cases the above equation really has no surprises. However, for adverse pressure gradients the matter is more complicated and up to 3 solutions are typically possible. The procedure above has been found to always pick up the non separated solution closest to the equilibrium one as long as possible, while the separated solution is taken only when it is the only solution to the equation. The algorithm might still get trapped in a positive solution branch when the actual solution is negative, but this seems largely ininfluential in the overall picture (considering also the nature of the solution, which is an approximate companion problem for a bc) and only affects the specific point where the switch of the solution branches actually happens. Of course, this reasoning is based on a certain class of common turbulent viscosity profiles; changing them to properly adapt to the non equilibrium case is actually the key in properly solving the problem.
In the next two posts in the series I will provide two closed form analytical solutions for the integrals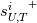 and
and 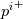 . The first will be the equivalent of the standard wall function, but for arbitrary N. The main advantage of its derivation in the present more rigorous framework is for the thermal case, where the resulting function just works for
. The first will be the equivalent of the standard wall function, but for arbitrary N. The main advantage of its derivation in the present more rigorous framework is for the thermal case, where the resulting function just works for 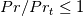 , while for the
, while for the  case involves the Jayatilleke function only for the determination of the switching position between the linear ang logarithmic part and not its actual value (where, however, it is still implicitly present).
case involves the Jayatilleke function only for the determination of the switching position between the linear ang logarithmic part and not its actual value (where, however, it is still implicitly present).
The second solution will be a reworking of the already presented Musker-Monkewitz solution. I will only provide a template of the solution here, but that template has practically shown to be easily extendable to arbitrary N. In particular, aside from a polynomial term, the same solution template works for arbitrary N, the difference being only in the function coefficients. I recall here that the Musker-Monkewitz solution is an all y+ solution that by a math trick can be used for arbitrary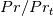 ratios (see, for example, here), the underlying turbulent voscosity has the correct
ratios (see, for example, here), the underlying turbulent voscosity has the correct 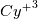 behavior near the wall and the correct
behavior near the wall and the correct  one in the logarithmic region. Also, it can be made the exact near wall behavior of the Spalart-Allmaras model by a trivial modification of any correct implementation of the model (more on this in a later post).
one in the logarithmic region. Also, it can be made the exact near wall behavior of the Spalart-Allmaras model by a trivial modification of any correct implementation of the model (more on this in a later post).
* Note that the definition used above has a very specific context, which is the evaluation of the integrals involving the turbulent viscosity ratio, because it is the variable used to parameterize it. In practice, it helps regularizing the implicit function for
definition used above has a very specific context, which is the evaluation of the integrals involving the turbulent viscosity ratio, because it is the variable used to parameterize it. In practice, it helps regularizing the implicit function for  . However, the true
. However, the true 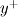 , only dependent on
, only dependent on  , remains the only relevant one for any other mean (including postprocessing).
, remains the only relevant one for any other mean (including postprocessing).
 from
from![\tau_w = \frac{\left[\left(U_p - U_w\right) \left(\frac{\mu}{y_p}\right) - y_p\sum_{i=0}^{N}\frac{F_U^i}{i+1}\left(\frac{{s_U^i}^+}{{y^+}^{i+2}}\right)\bigg\rvert_{y_p^+} \right]}{\left(\frac{{s_U^{-1}}^+}{y^+}\right)\bigg\rvert_{y_p^+}} \tau_w = \frac{\left[\left(U_p - U_w\right) \left(\frac{\mu}{y_p}\right) - y_p\sum_{i=0}^{N}\frac{F_U^i}{i+1}\left(\frac{{s_U^i}^+}{{y^+}^{i+2}}\right)\bigg\rvert_{y_p^+} \right]}{\left(\frac{{s_U^{-1}}^+}{y^+}\right)\bigg\rvert_{y_p^+}}](/Forums/vbLatex/img/37611d6af86567f69bd2cd9bc179341c-1.gif)
with analogous steps also required for the temperature and scalars. If one has a mean to univocally/externally determine
 , then velocity, temperature and scalars are all equivalent and the relation above (properly adjusted for temperature and scalars) can be used in one shot to determine the wall flux (or the wall value if the flux is known). For
, then velocity, temperature and scalars are all equivalent and the relation above (properly adjusted for temperature and scalars) can be used in one shot to determine the wall flux (or the wall value if the flux is known). For 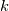 (turbulent kinetic energy) based turbulence models one can, for example, assume:
(turbulent kinetic energy) based turbulence models one can, for example, assume: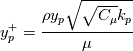
For the Spalart-Allmaras model instead, one can assume (it will be shown in a following post how this is, indeed, relevant):
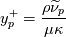
with
 the von Karman constant used in the model. These relations are strictly valid in equilibrium cases (
the von Karman constant used in the model. These relations are strictly valid in equilibrium cases (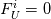 for all i) but are usually used in non equilibrium cases as well (there is a second advantage, besides non requiring iterations, that will be clear in a moment). If such variables/definitions are not available (say, in LES) one tipically defines:
for all i) but are usually used in non equilibrium cases as well (there is a second advantage, besides non requiring iterations, that will be clear in a moment). If such variables/definitions are not available (say, in LES) one tipically defines: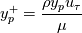
where:
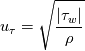
thus one ends up with an implcit non linear relation for
 that needs iterations to be resolved. Before going to the algorithmic part of these iterations, however, it is worth mentioning that the above choice for
that needs iterations to be resolved. Before going to the algorithmic part of these iterations, however, it is worth mentioning that the above choice for 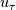 is largely inconvenient for non equilibrium flows, as the zero flux outcome is only possible when
is largely inconvenient for non equilibrium flows, as the zero flux outcome is only possible when 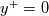 instead of, generally, when the numerator becomes 0 (which is the other advantage of the
instead of, generally, when the numerator becomes 0 (which is the other advantage of the 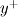 formulations based on turbulence variables). Following the relevant literature on the topic, we thus redefine the
formulations based on turbulence variables). Following the relevant literature on the topic, we thus redefine the 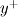 as follows*:
as follows*:![y_p^+ = \frac{\rho y_p}{\mu} \sqrt{\frac{\left|\tau_w\right|}{\rho} + \sum_{i=0}^{N}\left[\frac{\mu \left|F_U^i\right|}{\rho^2\left(i+1\right)}\right]^{\frac{1}{3}}} = \sqrt{\left|\theta_p\right|+\sum_{i=0}^{N}\left|F_p^i\right|^{\frac{2}{3}}} y_p^+ = \frac{\rho y_p}{\mu} \sqrt{\frac{\left|\tau_w\right|}{\rho} + \sum_{i=0}^{N}\left[\frac{\mu \left|F_U^i\right|}{\rho^2\left(i+1\right)}\right]^{\frac{1}{3}}} = \sqrt{\left|\theta_p\right|+\sum_{i=0}^{N}\left|F_p^i\right|^{\frac{2}{3}}}](/Forums/vbLatex/img/e71e43f1f1e973669705e4e4234300fa-1.gif)
where we have introduced the nondimensional parameters:
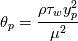
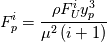
As both appear in the
 definition, it seems natural to transform the
definition, it seems natural to transform the  equation as well, by multiplying it with the factor
equation as well, by multiplying it with the factor 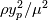 . The result is:
. The result is: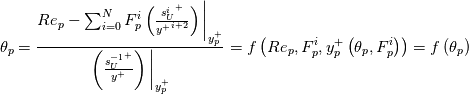
where we have introduced the additional nondimensional number:
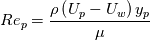
and highlighted the general dependence of the RHS of the
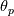 equation from
equation from 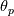 itself trough
itself trough  . Despite certainly having an extra
. Despite certainly having an extra 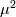 factor for all the terms (which could then be simplified to make all the numbers involved smaller), the advantage of this form is that being non dimensional it can be also solved once and for all for all the required nondimensional values and used at runtime as an interpolation table. Indeed, at this stage, it has to be reminded that the procedure is still applicable to generic
factor for all the terms (which could then be simplified to make all the numbers involved smaller), the advantage of this form is that being non dimensional it can be also solved once and for all for all the required nondimensional values and used at runtime as an interpolation table. Indeed, at this stage, it has to be reminded that the procedure is still applicable to generic 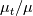 functions, and their integration might be costly as well. However, even in this case one would need to solve the equation above at least once for each set of relevant parameters. And having a nondimensional equation helps developing an iterative procedure.
functions, and their integration might be costly as well. However, even in this case one would need to solve the equation above at least once for each set of relevant parameters. And having a nondimensional equation helps developing an iterative procedure. I have found that with the constant non equilibrium term only, for different
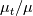 parameterizations, the above equation can be easily solved with a Newton-Raphson method with no more than 10 iterations (starting always from the same laminar solution, which is typically very wrong for high Re):
parameterizations, the above equation can be easily solved with a Newton-Raphson method with no more than 10 iterations (starting always from the same laminar solution, which is typically very wrong for high Re):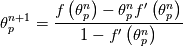
provided that
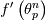 is set to 0 whenever it is equal or greater than 1. This specific modification, which reverts the method to fixed point iterations, is needed not only to avoid a possible division by 0, but also because the fixed point iterations will push the solution out of a problematic branch of the function.
is set to 0 whenever it is equal or greater than 1. This specific modification, which reverts the method to fixed point iterations, is needed not only to avoid a possible division by 0, but also because the fixed point iterations will push the solution out of a problematic branch of the function.I provide, again without proof, the expression for the derivative
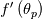 needed in the method:
needed in the method:![f'\left(\theta_p\right) = -\frac{SIGN\left(\theta_p\right)}{2\left(\frac{{s_U^{-1}}^+}{y^+}\right)\bigg\rvert_{y_p^+}} \left[f\left(\theta_p\right) {q^{-1}}^+ + \sum_{i=0}^{N}F_p^i {q^i}^+\right] f'\left(\theta_p\right) = -\frac{SIGN\left(\theta_p\right)}{2\left(\frac{{s_U^{-1}}^+}{y^+}\right)\bigg\rvert_{y_p^+}} \left[f\left(\theta_p\right) {q^{-1}}^+ + \sum_{i=0}^{N}F_p^i {q^i}^+\right]](/Forums/vbLatex/img/392f03ceddf360c22c89f5a395003c64-1.gif)
where the
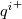 functions have been defined in the first post of this series.
functions have been defined in the first post of this series.In equilibrium and favourable pressure gradient cases the above equation really has no surprises. However, for adverse pressure gradients the matter is more complicated and up to 3 solutions are typically possible. The procedure above has been found to always pick up the non separated solution closest to the equilibrium one as long as possible, while the separated solution is taken only when it is the only solution to the equation. The algorithm might still get trapped in a positive solution branch when the actual solution is negative, but this seems largely ininfluential in the overall picture (considering also the nature of the solution, which is an approximate companion problem for a bc) and only affects the specific point where the switch of the solution branches actually happens. Of course, this reasoning is based on a certain class of common turbulent viscosity profiles; changing them to properly adapt to the non equilibrium case is actually the key in properly solving the problem.
In the next two posts in the series I will provide two closed form analytical solutions for the integrals
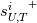 and
and 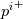 . The first will be the equivalent of the standard wall function, but for arbitrary N. The main advantage of its derivation in the present more rigorous framework is for the thermal case, where the resulting function just works for
. The first will be the equivalent of the standard wall function, but for arbitrary N. The main advantage of its derivation in the present more rigorous framework is for the thermal case, where the resulting function just works for 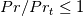 , while for the
, while for the  case involves the Jayatilleke function only for the determination of the switching position between the linear ang logarithmic part and not its actual value (where, however, it is still implicitly present).
case involves the Jayatilleke function only for the determination of the switching position between the linear ang logarithmic part and not its actual value (where, however, it is still implicitly present).The second solution will be a reworking of the already presented Musker-Monkewitz solution. I will only provide a template of the solution here, but that template has practically shown to be easily extendable to arbitrary N. In particular, aside from a polynomial term, the same solution template works for arbitrary N, the difference being only in the function coefficients. I recall here that the Musker-Monkewitz solution is an all y+ solution that by a math trick can be used for arbitrary
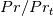 ratios (see, for example, here), the underlying turbulent voscosity has the correct
ratios (see, for example, here), the underlying turbulent voscosity has the correct 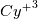 behavior near the wall and the correct
behavior near the wall and the correct  one in the logarithmic region. Also, it can be made the exact near wall behavior of the Spalart-Allmaras model by a trivial modification of any correct implementation of the model (more on this in a later post).
one in the logarithmic region. Also, it can be made the exact near wall behavior of the Spalart-Allmaras model by a trivial modification of any correct implementation of the model (more on this in a later post).* Note that the
 definition used above has a very specific context, which is the evaluation of the integrals involving the turbulent viscosity ratio, because it is the variable used to parameterize it. In practice, it helps regularizing the implicit function for
definition used above has a very specific context, which is the evaluation of the integrals involving the turbulent viscosity ratio, because it is the variable used to parameterize it. In practice, it helps regularizing the implicit function for  . However, the true
. However, the true 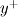 , only dependent on
, only dependent on  , remains the only relevant one for any other mean (including postprocessing).
, remains the only relevant one for any other mean (including postprocessing).Total Comments 0





