Uncategorized Entries with no category
|
|||
|
Posted in Uncategorized
Views 787
Comments 0

|
|
|||
|
Posted in Uncategorized
Views 665
Comments 0

|
|
|||
|
Posted in Uncategorized
Views 606
Comments 0

|
|
|||
|
Posted in Uncategorized
Views 715
Comments 0

|
|
|||
|
Posted in Uncategorized
Views 921
Comments 0

|

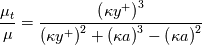


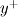
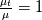
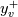

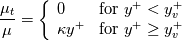

![\tau_w = \frac{\left[\left(U_p - U_w\right) \left(\frac{\mu}{y_p}\right) - y_p\sum_{i=0}^{N}\frac{F_U^i}{i+1}\left(\frac{{s_U^i}^+}{{y^+}^{i+2}}\right)\bigg\rvert_{y_p^+} \right]}{\left(\frac{{s_U^{-1}}^+}{y^+}\right)\bigg\rvert_{y_p^+}} \tau_w = \frac{\left[\left(U_p - U_w\right) \left(\frac{\mu}{y_p}\right) - y_p\sum_{i=0}^{N}\frac{F_U^i}{i+1}\left(\frac{{s_U^i}^+}{{y^+}^{i+2}}\right)\bigg\rvert_{y_p^+} \right]}{\left(\frac{{s_U^{-1}}^+}{y^+}\right)\bigg\rvert_{y_p^+}}](/Forums/vbLatex/img/37611d6af86567f69bd2cd9bc179341c-1.gif)
![\frac{d}{dy}\left[C_p\left(\frac{\mu}{Pr}+\frac{\mu_t}{Pr_t}\right)\frac{dT}{dy}\right]=F_T \frac{d}{dy}\left[C_p\left(\frac{\mu}{Pr}+\frac{\mu_t}{Pr_t}\right)\frac{dT}{dy}\right]=F_T](/Forums/vbLatex/img/0a6ecf7d1a227b166f5e9fa4142c0df0-1.gif)

